基于转矩损失的转矩分配方法和系统

1.本发明涉及电动汽车技术领域，特别是涉及基于转矩损失的转矩分配方法、基于转矩损失的转矩分配系统。


背景技术：

2.分布式轮毂电机驱动汽车由于轮毂内空间小，电机容易产生故障，从而影响其驱动性能，严重时会影响其汽车行驶稳定性。尤其是汽车在低附着路面下的轮毂电机转矩损失工况严重影响汽车操纵稳定性和行驶安全性，可以根据汽车稳定所需的附加横摆力矩对分布式驱动汽车四轮驱动转矩进行转矩分配，虽然具有稳定汽车的作用，但是未考虑转矩损失的情况，因此转矩的分配仍具有缺陷，未达到优化分配的效果。


技术实现要素：

3.基于此，有必要针转矩的分配因为未考虑转矩损失无法达到优化分配的问题，提供一种基于转矩损失的转矩分配方法、基于转矩损失的转矩分配系统。
4.为实现上述目的，本发明采用了以下技术方案：
5.基于转矩损失的转矩分配方法，其用于对汽车的多个车轮提供相应的驱动转矩分配值，以保持所述汽车的横向稳定性，所述基于转矩损失的转矩分配方法包括以下步骤：
6.根据所述汽车的附加横摆力矩δm和所述汽车的转矩损失系数，建立等式约束状态矩阵a
eq
和等式约束向量b
eq
；
7.根据所述汽车的优化分配的约束条件，建立二次型状态矩阵h和二次型状态向量c；
8.根据所述等式约束状态矩阵a
eq
、等式约束向量b
eq
、二次型状态矩阵h和二次型状态向量c通过二次规划函数计算出所述汽车的轮胎纵向力x，二次规划函数态向量c通过二次规划函数计算出所述汽车的轮胎纵向力x，二次规划函数其中，a是不等式约束函数状态矩阵，b是不等式约束向量；
9.将所述汽车的轮胎纵向力x与所述车轮的半径通过乘积计算获取所述车轮的驱动转矩分配值。
10.进一步的，所述优化分配的约束条件的计算方法包括以下步骤：
11.获取所述汽车的前右轮胎纵向力f
xfr
、所述汽车的前左轮胎纵向力f
xfl
、所述汽车的后右轮胎纵向力f
xrr
、所述汽车的后左轮胎纵向力f
xrl
、所述汽车的质心到前轴距离lf和所述汽车的质心到后轴距离lr；
12.计算所述汽车的附加横摆力矩约束：
13.δm＝(f
xfr-f
xfl
)lf+(f
xrr-f
xrl
)lr；
14.计算所述汽车的行驶总驱动力约束：f
x
＝f
xfl
+f
xfr
+f
xrl
+f
xrr
；
15.根据所述车轮的驱动转矩最大值，计算所述汽车的车轮的驱动转矩期望值约束：
tm≤t
max
。
16.进一步的，所述车轮的驱动转矩最大值的计算方法包括以下步骤：
17.获取所述汽车的轮毂电机的额定功率p
max
和所述汽车的轮毂电机的转速n；
18.计算所述车轮的驱动转矩最大值t
max
：
19.进一步的，所述二次规划函数的计算方法包括以下步骤：
20.获取所述汽车的轮胎纵向力f
xih
、所述汽车的轮胎侧向力f
yij
、所述汽车的轮胎垂直载荷f
zij
、所述汽车的车轮所在的地面附着系数μ；
21.根据路面附着系数计算轮胎纵向力的约束：
22.根据dugoff轮胎模型计算轮胎负荷率ρ
ij
：
23.根据所述汽车的轮胎负荷率建立二次目标函数：
24.其中，是轮胎负荷率的平方，e(ρ)是轮胎负荷率的平均均值，η是平均汽车轮胎负荷率的加权系数；
25.根据所述优化分配的约束条件，将所述二次目标函数转化成所述二次规划函数。
26.进一步的，所述二次型状态矩阵h的计算方法包括以下步骤：
27.获取所述汽车的前左轮胎垂直载荷f
zfl
、所述汽车的前右轮胎垂直载荷f
zfr
、所述汽车的后左轮胎垂直载荷f
zrl
、所述汽车的后右轮胎垂直载荷f
zrr
；
28.根据路面附着系数μ建立横摆力矩优化分配的二次型状态矩阵h：
[0029][0030]
进一步的，所述横摆力矩优化分配的二次型规划向量c的计算方法包括以下步骤：
[0031]
获取所述汽车的前左轮胎垂直载荷f
zfl
、所述汽车的前右轮胎垂直载荷f
zfr
、所述汽车的后左轮胎垂直载荷f
zrl
、所述汽车的后右轮胎垂直载荷f
zrr
、所述平均汽车轮胎负荷率的加权系数η；
[0032]
根据路面附着系数μ建立横摆力矩优化分配的二次型规划向量c：
[0033]
进一步的，所述等式约束状态矩阵a
eq
的计算方法包括以下步骤：
[0034]
获取所述汽车的左前轮转矩损失系数ε
fl
、所述汽车的右前轮转矩损失系数ε
fr
、所述汽车的左后轮转矩损失系数ε
rl
、所述汽车的右后轮转矩损失系数ε
rr
；
[0035]
根据所述汽车的质心到前轴距离lf和所述汽车的质心到后轴距离lr建立等式约束
状态矩阵a
eq
：
[0036]
进一步的，所述等式约束向量b
eq
的计算方法包括以下步骤：
[0037]
获取所述汽车的行驶总驱动力f
x
；
[0038]
根据所述汽车的附加横摆力矩δm建立b
eq
：b
eq
＝[δmf
x
]。
[0039]
进一步的，所述不等式约束函数状态矩阵a和不等式约束向量b的计算方法包括以下步骤：
[0040]
获取所述车轮的半径r、所述汽车的前左车轮驱动转矩最大值t
flmax
、所述汽车的前右车轮驱动转矩最大值t
frmax
、所述汽车的后左车轮驱动转矩最大值t
rlmax
、所述汽车的后右车轮驱动转矩最大值t
rrmax
；
[0041]
建立不等式约束函数状态矩阵a：
[0042]
建立不等式约束向量b：b＝[t
flmax t
frmax t
rlmax t
rrmax
]。
[0043]
本发明还包括基于转矩损失的转矩分配系统，所述系统工作时实现上述的基于转矩损失的转矩分配方法，所述基于转矩损失的转矩分配系统包括：
[0044]
约束系数矩阵计算模块，其用于根据所述汽车的附加横摆力矩δm和所述汽车的转矩损失系数，建立等式约束状态矩阵a
eq
和等式约束向量b
eq
；
[0045]
二次型状态矩阵计算模块，其用于根据所述汽车的优化分配的约束条件，建立二次型状态矩阵h和二次型状态向量c；
[0046]
二次规划函数计算模块，其用于根据所述等式约束状态矩阵a
eq
、等式约束向量b
eq
、二次型状态矩阵h和二次型状态向量c通过二次规划函数计算出所述汽车的轮胎纵向力x，二次规划函数其中，a是不等式约束函数状态矩阵，b是不等式约束向量；
[0047]
驱动转矩分配值计算模块，其用于将所述汽车的轮胎纵向力x与所述汽车的车轮的半径通过乘积计算获取所述汽车的车轮的驱动转矩分配值。
[0048]
本发明提供的技术方案，具有如下有益效果：
[0049]
本发明能够根据转矩损失发生的位置，在可用正常轮的基础上对转矩分配进行重构，保证汽车行驶安全，通过二次规划优化求解得到四轮最优驱动转矩，依据转矩损失系数重构四轮驱动转矩分配，控制轮毂电机输出转矩，从而促使汽车在电机转矩损失后依然能够具有稳定行驶的能力。
附图说明
[0050]
图1为本发明的基于转矩损失的转矩分配方法的流程图；
[0051]
图2为基于图1的转矩协调分配系统的结构示意图；
[0052]
图3为图1中模糊规则的三维仿真图；
[0053]
图4为基于图2的可拓控制转矩约束的可拓控制域的结构示意图；
[0054]
图5基于图2的横摆力矩控制系统的稳定域的结构示意图；
[0055]
图6为基于图2的考虑转矩损失的转矩分配系统仿真图；
[0056]
图7为基于图2的单轮转矩损失系统仿真图；
[0057]
图8为基于图2的两轮转矩损失系统仿真图；
[0058]
图9为基于图2的转矩协调分配系统的逻辑图。
具体实施方式
[0059]
下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。
[0060]
本发明的基于转矩损失的转矩分配方法解决了现有技术中转矩的分配因为未考虑转矩损失无法达到优化分配的问题。本发明通过转矩损失发生的位置，在可用正常轮的基础上对转矩分配进行重构，保证汽车行驶安全，通过二次规划优化求解得到四轮最优驱动转矩，依据转矩损失系数重构四轮驱动转矩分配，控制轮毂电机输出转矩，从而促使汽车在电机转矩损失后依然能够具有稳定行驶的能力。
[0061]
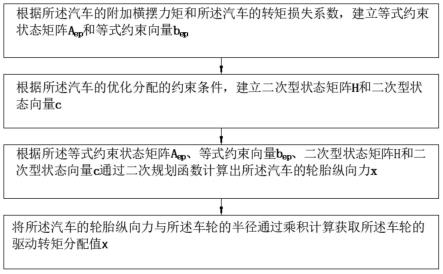
如图1所示，本实施例提供了基于转矩损失的转矩分配方法，包括以下步骤：
[0062]
根据所述汽车的附加横摆力矩δm和所述汽车的转矩损失系数，建立等式约束状态矩阵a
eq
和等式约束向量b
eq
；
[0063]
根据所述汽车的优化分配的约束条件，建立二次型状态矩阵h和二次型状态向量c；
[0064]
根据所述等式约束状态矩阵a
eq
、等式约束向量b
eq
、二次型状态矩阵h和二次型状态向量c通过二次规划函数计算出所述汽车的轮胎纵向力x，二次规划函数态向量c通过二次规划函数计算出所述汽车的轮胎纵向力x，二次规划函数其中，a是不等式约束函数状态矩阵，b是不等式约束向量；
[0065]
将所述汽车的轮胎纵向力x与所述车轮的半径通过乘积计算获取所述车轮的驱动转矩分配值。
[0066]
本实施例还提供了基于转矩损失的转矩分配系统，系统工作时实现上述基于转矩损失的转矩分配方法，所述系统包括约束系数矩阵计算模块，其用于根据所述汽车的附加横摆力矩δm和所述汽车的转矩损失系数，建立等式约束状态矩阵a
eq
和等式约束向量b
eq
；二次型状态矩阵计算模块，其用于根据所述汽车的优化分配的约束条件，建立二次型状态矩阵h和二次型状态向量c；二次规划函数计算模块，其用于根据所述等式约束状态矩阵a
eq
、等式约束向量b
eq
、二次型状态矩阵h和二次型状态向量c通过二次规划函数计算出所述汽车的轮胎纵向力x，二次规划函数其中，a是不等式约束函数状态矩阵，b是不等式约束向量；驱动转矩分配值计算模块，其用于将所述汽车的
轮胎纵向力x与所述汽车的车轮的半径通过乘积计算获取所述汽车的车轮的驱动转矩分配值。
[0067]
基于转矩损失的转矩分配方法应用于基于转矩损失的转矩分配系统，基于转矩损失的转矩分配系统包含在转矩协调分配系统内，下面对转矩协调分配系统进行具体说明。
[0068]
如图2所示，针对分布式驱动汽车在低附着路面下的轮毂电机转矩损失工况严重影响汽车操纵稳定性和行驶安全性，设计了一种转矩协调分配系统，主要由非线性误差反馈转矩控制系统、基于粒子群可拓控制转矩约束系统、基于汽车稳定性的横摆力矩控制系统和基于转矩损失的转矩分配系统构成。而非线性误差反馈转矩控制系统工作时则采用上述非线性误差反馈转矩控制系方法。
[0069]
下面对非线性误差反馈转矩控制系统进行具体说明：
[0070]
由于道路条件可能时刻变化，为了防止汽车产生轮胎打滑，增加稳定性控制策略的适用工况范围，采用模糊控制算法自适应调节车轮滑转率门限值。
[0071]
以汽车横摆角速度实际值与参考值的偏差δωz(δωz＝ω
z-ωz′
)和当前车轮滑转率值s作为输入，滑转率门限值s
max
作为输出，进行滑转率门限值模糊规则设置，例如车轮滑转率值s和横摆角速度越大的情况，汽车急需减小车轮滑转保证汽车稳定性，此时模糊控制输出的车轮滑转率门限值越小。依据多次仿真试验建立的模糊逻辑规则表如下表所示。
[0072]
滑转率门限值模糊规则表
[0073][0074]
由上述模糊规则以及相应的输入输出隶属度函数得到的模糊规则三维效果图如图3所示可以根据参数估计情况判断并输出当前工况相适应的滑转率门限值，进而据此进行车轮防滑控制约束车轮驱动转矩。
[0075]
基于模糊控制的滑转率门限值，设计非线性误差反馈转矩控制系统，以获得防止车轮打滑的期望转矩。非线性误差反馈控制原理是将误差进行非线性组合，然后输出转矩控制需求，图1所示，其中非线性负反馈控制的输入为车轮滑转率估计值与滑转率门限值的偏差e1、车轮驱动转矩实际值与转矩期望值的偏差e2，经过非线性组合两者误差计算出驱动转矩调整值te，以防止车轮打滑。β为质心侧偏角，所设计的非线性误差反馈控制数学表达
式为：其中，u0为非线性控制律，k0为增益系数，c0为阻尼系数，h0为采样时间，补偿因子b0＝1/j
ω
，(车轮转动惯量0.9kg
·
m2)，调节系数r0＝0.05/h0，r0的作用是调节该非线性反馈控制系统的控制力度，对于上述数值，可以由经验值确定，也可以经过多次试验确定，fst(
·
)是最速控制综合函数，为
[0076]
下面对基于粒子群可拓控制转矩约束系统进行具体说明：
[0077]
考虑防止车轮打滑设计转矩约束控制，因为不同工况下车轮转矩输出约束需求并不相同，因此采用可拓控制理论分别划分可拓控制域，实现随路面工况的变化自适应调整车轮转矩约束模式；可拓控制域的划分如图4所示，在可拓集合中原点与特征量的连线，与可拓域、经典域的边界交点从左至右分别为q1、q2、q3、q4，经典域中汽车车轮滑转率较小且汽车质心侧偏角较小，汽车处于路面附着条件较好的工况，此时不需要车轮打滑的转矩约束。可拓域中汽车车轮滑转率和质心侧偏角有增大趋势，此时需要对转矩分配加以约束限制，并将状态保持在可拓域最佳，防止转矩继续增大进入非域。非域中车轮滑转率与质心侧偏角较大，汽车即将失稳或已进入失稳状态，此时需要严格约束车轮转矩，尽可能保证汽车安全稳定性。
[0078]
可拓控制域需要划分可拓集并确定各区域边界，进而确定各控制区域的车轮转矩约束模式，其设计步骤如下：
[0079]
(1)选择特征量
[0080]
特征量用来表示车轮打滑状态和汽车稳定状态。因此为了区分经典域、可拓域和非域的车轮滑转及行驶稳定性边界和区域，选择车轮滑转率值s和汽车的实际质心侧偏角β作为特征量，两者组成q(s,β)。
[0081]
(2)划分可拓集
[0082]
首先是经典域边界的划分，经典域边界划分相对容易，将横摆角速度增益的线性区边界为实际质心侧偏角经典域边界。通过拟合关系计算出线性区实际质心侧偏角最大值，此时实际质心侧偏角的值即为经典域边界β1。前轮转角极限值与车速的经验公式为：
[0083][0084]
其中，a
10
，b
10
，c
10
和d
10
为拟合参数，分别为0.05，0.07，0.6和13.3；将计算出的线性
区前轮转角最大值δ
max
代入车辆二自由度模型可计算出经典域边界β1。
[0085]
车轮滑转率的经典域边界s1以前述模糊控制输出的滑转率门限值为界限，即s1＝s
max
。当车轮滑转率小于滑转率门限值时，则认为车轮滑转状态稳定，处于经典域中。
[0086]
其次划分可拓域边界。粒子群算法不依赖于优化问题本身的严格数学性以及目标函数和约束条件精确的数学描述，只需要设计相应的评价函数，可拓域边界是一个二维边界，维度较小，因此可拓域边界的划分采用粒子群算法，迭代寻找最优边界。该算法在每一次迭代中，粒子不断根据个体最优解pi和目前为止的种群最优解pg两个极值更新自己。进而依据下式更新粒子速度与位置：
[0087][0088][0089][0090]
其中，是粒子在第k代的速度和位置，是粒子最大速度，其值过大容易飞过最优解，rand()是大于0小于1的随机数，学习因子取c1＝c2＝2，τ是惯性权重，其用来平衡局部和全局最优值，设计τ为如下式所示：
[0091]
其中，最大权重τ
max
＝1.4，最小权重τ
min
＝0.4，t
gen
为迭代次数。
[0092]
设置适应度函数为：由此可见，粒子群算法确定可拓域边界的具体流程为：
[0093]
步骤1.获取所述车轮的横摆角速度实际值ωz，根据所述横摆角速度实际值ωz和所述实际质心侧偏角β设置适应度函数其中，v
x
是所述车轮的车速，μ是路面附着系数，g是重力加速度；
[0094]
步骤2.以所述汽车其中一个车轮作为目标个体，所述汽车的所有车轮作为种群，将每个车轮的横摆角速度实际值ωz和对应的实际质心侧偏角β作为粒子参数，组成粒子，将所有粒子组成粒子群；
[0095]
步骤3.获取所述种群在实际路面附着系数下的历史最优状态的粒子参数，作为历史种群最优解，获取所述目标个体在所述实际路面附着系数下的历史最优状态的粒子参数，作为历史个体最优解；
[0096]
步骤4.以所述目标个体的实际粒子参数作为目标粒子，将所述目标粒子通过所述适应度函数计算出所述目标粒子的适应值；
[0097]
步骤5.将所述目标粒子的适应值与历史个体最优解的适应值进行对比，若所述目标粒子的适应值大于所述历史个体最优解的适应值，则将所述目标粒子的粒子参数替代所述历史个体最优解的粒子参数，更新个体最优解，若所述目标粒子的适应值小于所述历史个体最优解的适应值，则所述历史个体最优解的粒子参数保持不便；
[0098]
步骤6.将所述目标粒子的适应值与所述历史种群最优解的适应值进行对比，若所述目标粒子的适应值大于历史种群最优解的适应值，则将所述目标粒子的粒子参数替代历
史种群最优解的粒子参数，更新种群最优解，若所述目标粒子的适应值小于历史种群最优解的适应值，则所述历史种群最优解的粒子参数保持不便；
[0099]
步骤7.根据所述个体最优解和新的种群最优解对所述目标粒子的粒子参数进行迭代更新，判断迭代次数是否达到预设的最大迭代数，否则将更新后的目标粒子返回步骤3，是则停止迭代，将所述目标粒子迭代结束后的横摆角速度实际值通过滑转率计算公式计算出滑转率最优值s2，将所述目标粒子迭代结束后的的实际质心侧偏角作为最优质心侧偏角β2。
[0100]
(3)关联函数设计
[0101]
根据特征量在控制域中的位置和距离设计关联函数，特征点到可拓域的可拓距如下：
[0102][0103]
其中，ck是可拓域区间，则关联函数k(s)为：
[0104]
其中，cj是经典域区间，这样可更便捷地通过关联函数k(s)计算结果判断特征量所在域。
[0105]
(4)测度模式划分
[0106]
可通过关联函数k(s)判断特征量的测度模式，即测度模式m1＝{s|k(s)＞1}时特征量在经典域；测度模式m2＝{s|0k(s)≤1}时特征量在可拓域；测度模式m3＝{s|k(s)＜0}时特征量在非域。
[0107]
因此在m1测度模式下，无需考虑车轮打滑的转矩约束限制，此时转矩只受轮毂电机本身峰值转矩约束，即p
max
为轮毂电机额定功率，n为电机转速。
[0108]
在m2测度模式下，需要考虑一定程度的车轮打滑情况。根据非线性误差反馈转矩控制系统输出的驱动转矩调整值te设计转矩最大值约束t
max
为：t
max
＝[k(s)+1]te。
[0109]
在m3测度模式下，车轮滑转情况严重，质心侧偏角也进入失稳状态，此时设计转矩最大值约束t
max
为：t
max
＝te。
[0110]
其通过车轮滑转率值和实际质心侧偏角的可拓域划分判断车轮输出转矩的约束模式，并通过粒子群算法对不同附着条件路面搜索最优可拓域边界。
[0111]
下面对基于汽车稳定性的横摆力矩控制系统进行具体说明：
[0112]
轮毂电机输出转矩的损失会造成汽车横摆力矩的突变。这一过程中产生过大的横摆力矩，有可能使汽车迅速改变航向角以及行驶轨迹，进入不稳定工况，进而增加行驶危险性。因此，应该有与之相适应的横摆力矩约束对汽车横摆运动优化控制及驱动转矩分配控制策略，从而保证汽车行驶的稳定性。
[0113]
先需要根据汽车状态确定控制边界，即确定稳定性控制判据，而汽车稳定性判据决定了横摆力矩控制系统启动与否，采用实际质心侧偏角-实际质心侧偏角速度(β-v
β
)相平面作为汽车稳定性判据。
[0114]
采用双线法和极限环法对汽车稳定区域进行划分，即在双线法划出的区域内再增
加一个与两直线相切的椭圆，将该椭圆作为稳定性区域，示意图如图5所示，直线l1和l2为双线法确定的相平面稳定边界，而椭圆与l1和l2相切，其内部为最终确定的稳定域，因此由两直线和椭圆方程联立得两切点，最终计算出椭圆的长短半轴a和b：
[0115][0116]
其中，c
11
和c
22
根据实际相图确定，由上述方法便获得汽车稳定性判据，即如果汽车状态处于椭圆稳定区域以外，此时需要横摆力矩控制系统作用输出恢复稳定的附加横摆力矩，以供转矩分配层分配转矩使汽车恢复稳定。通过该方法获得不同路面附着系数下的稳定区域椭圆半轴长度如下表所示：
[0117]
稳定边界参数表
[0118][0119]
根据表中参数得到稳定边界椭圆半轴随着路面附着系数变化的拟合公式为：
[0120][0121]
采用滑模控制算法计算汽车稳定所需附加横摆力矩，滑模控制律和滑模面会根据被控系统的特性要求随之改变，与系统的扰动和其他参数无关。
[0122]
首先计算汽车参考横摆力矩，由于道路条件多种多样，其路面附着系数也不断变化，因此由汽车理论可知，汽车横摆角速度和质心侧偏角受附着条件约束，可得二者根据附着条件的约束为：
[0123]
则汽车的理想质心侧偏角βd和横摆角速度ωd分别为：
[0124]
[0125][0126]
其中为汽车稳定性系数，v
x
是车速，δ是前轮转角，lr是质心到后轴距离，lf是汽车的质心到前轴距离，l是汽车的车轮的轴距，k2是汽车的后轮侧偏刚度k2，k1是汽车的前轮侧偏刚度，m是整车质量
[0127]
设计的滑模函数为：u＝(ω
z-ωd)+h2(β-βd)，
[0128]
对滑模控制率u求导，求导公式为：
[0129]
滑模控制器趋近律为：其中，β是汽车的实际质心侧偏角，ε是汽车的转矩损失系数，h1是滑模控制率计算的的加权系数，h2是滑模控制趋近率计算的加权系数h2。
[0130]
由于滑模控制存在抖振问题，可采用滤波方法，对滑模控制的切换函数使用低通滤波器，得到平滑的信号，降低系统的抖振。最终联立车身三自由度模型得出维持汽车稳定行驶需求的附加横摆力矩为：
[0131][0131]
其中，fyfr是前右轮胎侧向力，fyrr是后右轮胎侧向力，fyfl是前左轮胎侧向力，f
yrl
是后左轮胎侧向力。
[0132]
下面对基于转矩损失的转矩分配系统进行具体说明：
[0133]
为保证汽车横摆稳定性，依据基于汽车稳定性的横摆力矩控制系统得出的汽车稳定所需附加横摆力矩对分布式驱动汽车四轮驱动转矩进行转矩分配。四轮转矩分配采用二次规划算法。根据车轮动力学相关理论，车轮轮胎力受到附着椭圆的限制，车轮纵向力越大留给横向力的余裕就越小，汽车转向时的横向稳定性受到影响。因此采用轮胎负荷率约束车轮转矩，保证汽车横向稳定性，以汽车具有四个车轮为例。
[0134]
首先确认优化目标函数，根据dugoff轮胎模型计算轮胎力，其与轮胎附着力的关系为：
[0135][0136]
其中，f
xij
是轮胎纵向力，f
yij
是轮胎侧向力，f
zij
是轮胎垂直载荷
[0137]
设置轮胎负荷率为：
[0138][0139]
其中i∈{f,r}表示前后，j∈{l,r}表示左右。
[0140]
轮毂电机驱动转矩可以直接控制，轮胎纵向力与侧向力都由附着力提供，保证横向力就要减小纵向力，因此以纵向力为主设置二次目标函数为：
[0141][0142]
其中e(ρ)表示轮胎负荷率的平均均值，加入e(ρ)的目的是使每个轮胎负荷率能够
接近，可以提高每个轮胎的利用率，η是加权系数，用来协调两部分优化目标占比。
[0143]
随后确定优化分配的约束条件，主要是附加横摆力矩与纵向驾驶员模型输出驱动力的等式约束和考虑车轮滑转的最大转矩约束的不等式约束，所建立约束如下式所示：
[0144][0145]
其中f
x
为汽车行驶总驱动力，p
max
为轮毂电机额定功率，n为电机转速，s为车轮滑转率，tm驱动转矩实际值，f
xfr
是前右轮胎纵向力，f
xrr
是后右轮胎纵向力，f
xfl
是前左轮胎纵向力，f
xrl
是后左轮胎纵向力。
[0146]
最后确定优化分配算法，利用二次规划理论优化分配上层横摆力矩，目标函数转化为标准二次型，二次规划函数为：
[0147]
其中x＝[f
xfl
,f
xfr
,f
xrl
,f
xrr
]
t
表示矩阵转置，由不等式约束和二次规划函数可推出二次规划h矩阵和c矩阵为：
[0148][0149][0150]fzfl
是汽车的前左轮胎垂直载荷，f
zfr
是汽车的前右轮胎垂直载荷，f
zrl
是汽车的后左轮胎垂直载荷，f
zrr
是汽车的后右轮胎垂直载荷，由不等式约束函数可得a，b分别为：
[0151][0152]
其中，r车轮的半径，t
flmax
是汽车的前左车轮驱动转矩最大值，t
frmax
是汽车的前右车轮驱动转矩最大值，t
rlmax
是汽车的后左车轮驱动转矩最大值，t
rrmax
是汽车的后右车轮驱动转矩最大值，由此可见，ax≤b不等式约束是一个仿射函数，a
eq
x＝b
eq
等式约束也是一个仿射函数，这与凸二次规划问题的特征一致，因此该二次规划问题为一个凸二次规划问题。
[0153]
此外由于四轮轮毂电机存在转矩损失的情况，需要根据转矩损失程度重构转矩分配，ε＝[ε
fl
,ε
fr
,ε
rl
,ε
rr
]
t
，则对于二次规划函数，根据不等式约束函数并将ε整合至约束系
数矩阵a
eq
和b
eq
中，得
[0154][0155]beq
＝[δm f
x
]
[0156]
对二次规划函数求解得到四轮最优驱动转矩后，进一步依据转矩损失系数重构四轮驱动转矩分配，控制轮毂电机输出转矩，从而促使汽车在电机转矩损失后依然能够具有稳定行驶的能力。
[0157]
对于转矩协调分配系统进行仿真分析，首先初步验证考虑转矩损失的转矩分配策略能否在轮毂电机转矩损失时保证汽车的行驶稳定性。选择双移线工况，路面附着系数设置为0.85，仿真设置右前轮毂电机损失降至60％转矩输出，仿真起始车速和目标车速均设为60km/h。结果如图6所示。其中考虑转矩损失的转矩分配策略表示为tdtl(torque distribution when torque loss)。从图6(a)中可以看出，右前轮转矩损失会导致汽车有一个偏右行驶的横摆角速度，而在对四轮重新分配转矩后，汽车横摆角速度可以跟随期望值并保证汽车安全行驶，提高了汽车的操纵性。从图6(b)中可以看出，汽车右前轮转矩损失后质心侧偏角也开始增大，严重影响汽车稳定性，而考虑转矩损失的转矩分配策略对四轮转矩重构，减小了质心侧偏角实际值与参考值的误差，使汽车稳定性大大增加。从图6(c)中可以看出，当汽车右前轮发生转矩损失，汽车不仅操纵稳定性变差，车速也有一定程度损失，而考虑转矩损失的转矩分配策略可以使汽车在双移线动作中车速降低相对更小，一定程度上提高了汽车的动力性。因此，可以分析得出考虑转矩损失的转矩分配策略在良好附着条件的路面时能够发挥保证汽车行驶安全性，操纵稳定性和一定的动力性。
[0158]
进行单轮转矩损失仿真验证时，选择双移线工况仿真试验，设置右前轮转矩损失降至60％，设置路面附着系数为0.3，起始车速和目标车速均为60km/h，仿真结果如图7所示。其中考虑转矩损失的转矩分配策略表示为tdtl。考虑转矩损失的车轮防滑约束转矩协调分配策略表示为tdsrtl(torque distribution for slip restraint when torque loss)。从两种控制策略的对比仿真结果中可以看出，图7(b)中，相比于未考虑转矩约束的转矩分配策略(tdtl)，考虑车轮滑转约束的转矩协调分配策略(tdsrtl)可以使汽车横摆角速度响应更快，汽车操纵性更好，即能更快得响应驾驶员的转向需求。图7(c)中在10.45s时刻未考虑转矩约束的转矩分配策略的质心侧偏角为-2.845
°
，而考虑车轮滑转约束的转矩协调分配控制策略的质心侧偏角为-2.446
°
，减小了14.02％，同时还可以消除了汽车质心侧偏角的抖动，提高了汽车的行驶稳定性。图7(d)中四轮转矩输出曲线可以看出，右前轮转矩损失后，左前轮也随之降低驱动转矩，而右后轮根据横摆力矩控制需求相应地增大驱动转矩，但是在考虑车轮滑转的约束控制下，右后轮在转矩增大的过程中也会随时降低驱动转矩以防止车轮打滑，保证汽车行驶安全。图7(e)中虽然车轮转矩被限制，一定程度上降低了汽车驱动转矩，但汽车车速下降并不多，只在双移线动作过程中低了0.5km/h左右。总的来说，当右前轮有转矩损失时，所提出的考虑车轮滑转的协调转矩分配控制策略重新分配转矩，保证了汽车稳定所需的横摆力矩，保证了汽车行驶安全。
[0159]
进行两轮转矩损失仿真验证时，设计两轮发生转矩损失工况，对所提转矩协调分配控制策略进行验证。选择双移线仿真试验。设置同侧两轮转矩损失，右前轮转矩损失降至80％，右后轮转矩损失降至50％，路面附着系数为0.3，起始车速和目标车速都为60km/h，仿
真结果如图8所示。从同侧两轮转矩损失的仿真对比结果中看出，图8(b)中未考虑转矩约束的转矩分配策略(tdtl)在双移线动作第二次换道时发生了一定程度的侧滑，使汽车在这段时间处于较为危险的行驶状态，而考虑车轮滑转的转矩协调分配控制策略(tdsrtl)改善了侧滑现象保证了汽车行驶安全。图8(c)中可以看出，虽然未考虑转矩约束的转矩分配策略在10s以前能够减小汽车质心侧偏角保证汽车稳定性，但是导致第二次换道时车轮打滑反而增大了质心侧偏角，而转矩协调分配控制虽然在可拓判断下一定程度上约束了转矩输出，但是同时控制了车轮侧滑，整体上保证汽车稳定性。图8(d)四轮转矩可以看出，由于右侧两轮都发生了转矩损失，无法像单轮损失那样增大异轴同侧转矩弥补横摆力矩。此时左侧两轮转矩也降低并跟随右侧车轮转矩的变化，同时左侧车轮微调转矩输出以维持横摆力矩的稳定。图8(e)中可以看出，未考虑转矩约束的转矩分配策略最低车速为56.5km/h，而转矩协调分配控制下的汽车车速可以保持在57～60km/h之间，一定程度上使汽车的动力性得到保证。
[0160]
经过验证可得知，对于整个转矩协调分配系统，通过对汽车四轮电机转矩进行分配，保证汽车在电机转矩损失时能稳定安全行驶。
[0161]
以上所述实施例的各技术特征可以进行任意的组合，为使描述简洁，未对上述实施例中的各个技术特征所有可能的组合都进行描述，然而，只要这些技术特征的组合不存在矛盾，都应当认为是本说明书记载的范围。
[0162]
以上所述实施例仅表达了本发明的几种实施方式，其描述较为具体和详细，但并不能因此而理解为对发明专利范围的限制。应当指出的是，对于本领域的普通技术人员来说，在不脱离本发明构思的前提下，还可以做出若干变形和改进，这些都属于本发明的保护范围。因此，本发明专利的保护范围应以所附权利要求为准。