一种四轮毂电机驱动智能汽车的转矩分配控制方法

本发明属于纯电动汽车控制领域，具体涉及一种四轮毂电机驱动智能汽车的转矩分配控制方法。

背景技术：

1、许多学者对四轮毂电驱动汽车的稳定性控制采用分层控制策略，其中上层控制主要是为获取车辆稳定行驶的广义目标力或力矩。由于四轮毂电机驱动汽车的四个车轮是相互独立的，为了实现上层控制策略而对转矩进行分配，属于下层控制。目前主要分配方法有平均分配、动态载荷分配和最优分配三种。

2、吉林大学的jin l等将纵向车速pid控制得到的总纵向力矩平均分配给各个车轮，然后将上层期望的横摆力矩根据车轮转向角分配到左右轮，保证汽车纵向驾驶性和横向操纵性的动力需求。图西理工大学的aria n等根据轮胎动态载荷转移将上层的控制力矩分配给四个轮毂电机，设计了基于滑移率的滑模控制器对转矩进行修正，通过仿真结果得出汽车侧向加速度减小，横摆角速度能够很好地跟踪参考值。同时，汽车质心侧偏角减小，汽车操纵稳定性进一步提高。索邦大学的laghmara h等根据轮胎垂直载荷转移的比值对上层控制的纵向力矩和横摆力矩进行分配，改善了汽车跟踪期望运动状态的能力。吉林大学的renb等将四轮毂电机的转矩作为mpc控制系统的控制量，其控制目标函数不仅考虑了汽车状态跟踪期望状态的性能，还考虑了轮毂电机最大扭矩、轮胎的滑移率、转矩变化量以及汽车转向行驶的需求。计算机仿真结果得出合理分配转矩使控制器控制效果良好，满足了驾驶员的期望。上海交通大学的shi y和yu f等忽略轮胎侧向力对横摆力矩产生的影响，认为期望横摆力矩是由轮胎纵向力产生。单个车轮的扭矩分配可以看作是一个非线性约束优化问题，选择能量损耗和纵向控制误差最小为目标函数，使用序列二次规划(sequencequadratic programming，sqp)方法求解。与上层控制结合进行仿真验证，结果表明提高了汽车在典型变道工况的操纵稳定性，减小驾驶员的驾驶负荷。最优控制算法是研究人员当前研究轮毂电机转矩分配控制的优先选择算法。分布式电驱动汽车属于执行器冗余系统，可转化为一个约束条件下的优化问题。采用最优分配算法可以将侧向力和横摆力矩以最优值分配到执行器上，充分发挥执行器的作用。重庆大学的hu j等将轮毂电机效率最高作为目标函数，将轮毂电机的最大扭矩和前轮的驱动分配系数作为约束，对目标控制力和力矩进行分配，该控制算法可使电机最高效率达89.49％，比平均分配的效率提高0.42％。吉林大学的武冬梅将节能和安全作为整车动力学综合控制的目标，利用最优分配算法综合分配了转矩，不仅提高了汽车转向行驶的稳定性，也提高了轮毂电机的效率。

3、平均分配和动态载荷分配属于直接分配控制，计算量小，响应快，但是忽略了执行器的约束条件，不能充分发挥执行器的作用，系统的整体效果变差。sqp是基于数学规划算法的，可以充分考虑控制系统的约束条件，精确度高，但是算法相对比较复杂。此外，在轮毂电机转矩分配控制中，针对约束的优化问题，未能全面考虑执行器的约束条件，而且多数是对前、后轴进行展开研究。轮毂电机驱动智能汽车的实际行驶环境复杂多变，转矩的最优分配不仅要满足汽车行驶的操纵稳定性，还需考虑能量损耗和续航里程问题，所以本发明设计一种四轮毂电机驱动智能汽车的转矩分配控制方法，可同时兼顾汽车稳定性和经济性的最优分配算法。

技术实现思路

1、本发明要解决的技术问题是克服上述现有技术存在的缺陷而提供一种四轮毂电机驱动智能汽车的转矩分配控制方法，将可拓控制理论应用到四轮毂电机驱动智能汽车的转矩分配控制中，根据汽车的行驶状态动态分配基于节能和稳定性的权重系数，保证汽车节能和稳定性行驶。

2、为实现上述的目标，本发明的技术方案为：

3、一种四轮毂电机驱动智能汽车的转矩分配控制方法，其具体步骤包括：

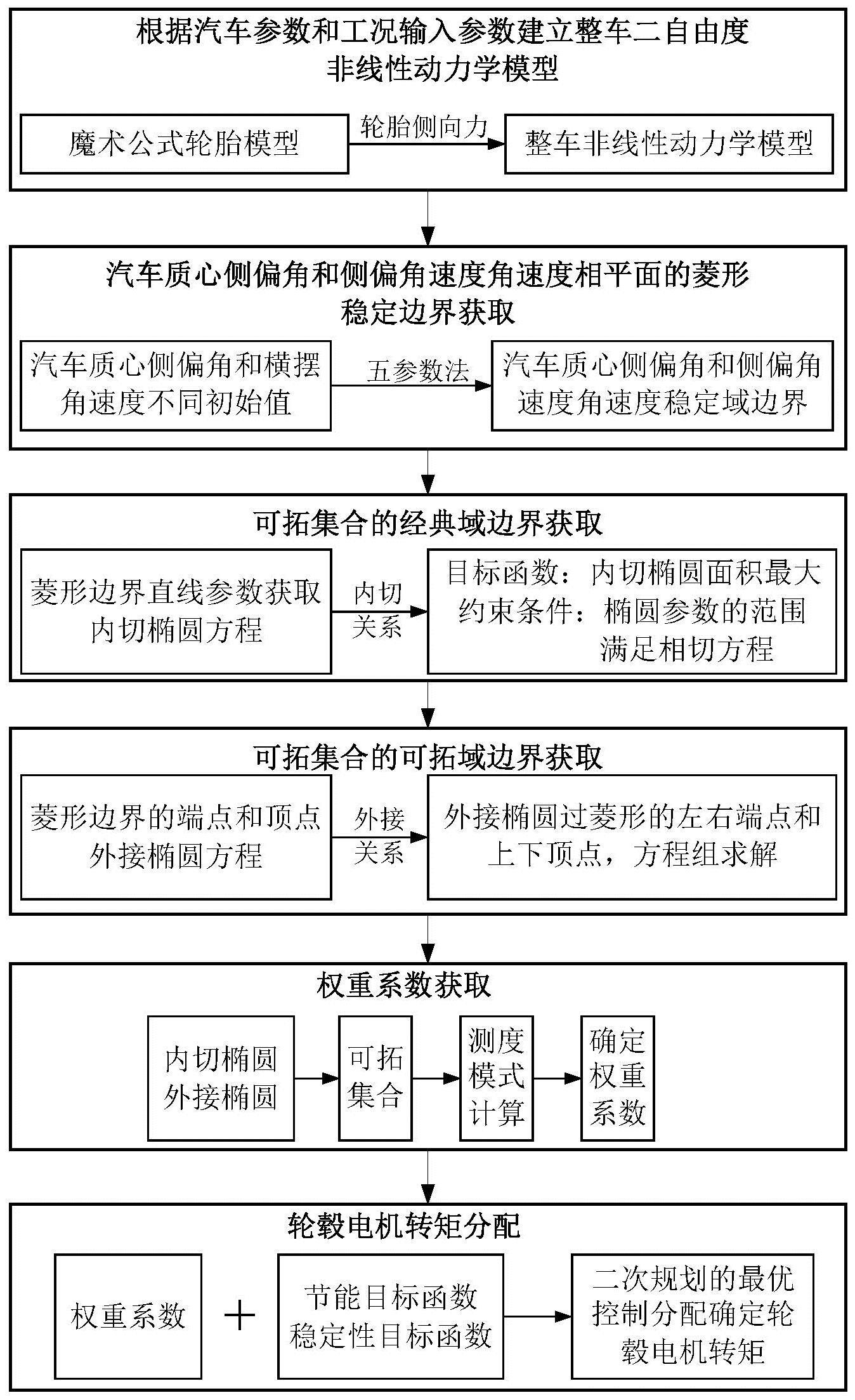
4、1)首先根据汽车自身参数和工况输入参数建立整车二自由度非线性动力学模型，利用二自由度动力学模型绘制整车质心侧偏角-侧偏角速度相平面图，横坐标是质心侧偏角，纵坐标是质心侧偏角速度；

5、2)根据汽车行驶工况的实际质心侧偏角、质心侧偏角速度和稳定点，采用五参数法确定菱形稳定区域，根据菱形稳定域边界线满足的条件，获取菱形稳定域边界；

6、3)根据菱形边界的四条直线分别与内椭圆边界相切的关系，设计内切椭圆的面积最大为目标函数，确定圆心、长半轴和短半轴的范围为约束条件，利用matlab的fmincon函数获取内切椭圆，即可拓集合的经典域；

7、4)根据菱形边界的四条直线两两之间的交点分别与外椭圆边界重合，利用matlab求解关于四条直线方程和外接椭圆方程的组成方程组，获取外接椭圆，即可拓集合的可拓域；

8、5)选取汽车质心侧偏角和质心侧偏角速度为两个特征量，根据可拓距求解方法，划分测度模式并确定权重系数；

9、6)分别确定基于汽车稳定性和节能的轮毂电机转矩分配目标函数，根据步骤5)中确立的权重系数，最终获取总目标函数，根据汽车需求总的力、力矩和行驶约束设置目标函数实现的约束条件，通过matlab软件编程进行最优求解，获得各个轮毂电机的转矩。

10、进一步的，步骤1)具体包括：

11、1.1根据所述汽车参数，利用魔术公式建立非线性轮胎模型，即：

12、根据公式fy＝dsin{carctan[bα-e(bα-arctan(bα))]}获取轮胎侧向力；

13、其中，fy为轮胎侧向力，α为轮胎侧偏角，b、c、d和e是是关于轮胎垂向载荷和外倾角的函数，可通过拟合轮胎模型参数得到；

14、1.2根据步骤1.1中的轮胎侧向力建立汽车二自由度非线性动力学模型，即：

15、忽略轮胎纵向力，假设后轮转角为零，根据公式建立汽车非线性动力学模型；

16、其中，fyf和fyr分别为前、后轮胎的侧向力，m为整车质量，v为整车车速，iz为整车转动惯性量，lf和lr分别为整车质心至前、后轴的距离，β为汽车质心侧偏角，γ为整车横摆角速度；

17、1.3采用汽车质心侧偏角和侧偏角速度分别作为相平面的横坐标和纵坐标，给定汽车质心侧偏角和横摆角速度不同的初始值，通过设置不同的车轮转角、车速和路面附着系数，得到不同行驶工况下的汽车质心侧偏角-侧偏角速度相平面图；

18、进一步的，步骤2)具体包括：

19、2.1利用五参数法确定菱形稳定边界，其中稳定点是不同初始状态下相轨迹汇集的焦点，临界相轨迹收敛到焦点时，与横坐标和纵坐标的交点分别为菱形的左端点右端点上顶点和下顶点连接端点和顶点合成菱形稳定边界；

20、2.2将步骤2.1中的左端点(-β1，0)、右端点(β2，0)、上顶点和下顶点带入质心侧偏角和偏角角速度的稳定域边界关系式(m＝1～4)进行方程组求解，确定菱形边界直线的参数c1m、c2m；

21、进一步，步骤3)具体包括：

22、根据菱形稳定区域边界与内切椭圆的相切关系，将内切椭圆的面积定义为目标函数：

23、j内＝min(-πr1r2)

24、约束条件为：

25、其中，r1和r2分别是内切椭圆的长半轴和短半轴，a1和b1分别是内切椭圆的圆心横坐标和纵坐标。

26、通过matlab软件提供的fmincon函数求解内切椭圆的长半轴、短半轴和圆心位置，得菱形的内切椭圆，即可拓集合的经典域。

27、进一步，步骤4)具体包括：

28、根据外接椭圆公式并将菱形稳定区域边界的两个端点和两个顶点带入，求解方程组可得菱形稳定区域外接椭圆的长半轴、短半轴和圆心，确定菱形的外接椭圆，即可拓集合的可拓域，可拓域之外是非域，最终确定可拓集合。

29、其中，ra和rb分别是外接椭圆的长半轴和短半轴，o1和o2分别是外接椭圆的圆心横坐标和纵坐标。

30、进一步的，步骤5)具体包括：

31、利用传感器实时测得汽车质心侧偏角和侧偏角速度，由此得到二维特征空间的特征点，转换成一维可拓集合，求得可拓距，利用关联函数公式确定特征点所在的区域，k(s)≥1时，ηe＝1，ηs＝0；0≤k(s)＜1时，ηe＝k(s)，ηs＝1-k(s)；k(s)＜-1时，ηe＝0，ηs＝1。

32、其中，p是质心侧偏角和侧偏角速度在可拓集合中的特征点，p1、p2、p3和p4分别是p点与圆心的连接并两边延长分别与可拓域边界、经典域边界的交点。

33、进一步的，步骤6)具体包括：

34、基于稳定性和节能的轮毂电机转矩分配控制目标函数公式分别为

35、

36、

37、约束条件：

38、

39、其中，txij(i＝f～r，j＝l～r)为各轮毂电机的转矩，μ为路面附着系数，rij为轮胎滚动半径，fzij为轮胎垂直载荷，ploss，ij为各轮毂电机损失功率，其表达式为tx为纵向总需求力矩，δm为附加的直接横摆力矩，bf和br为前、后轮距，δf为前轮转角，tmax为轮毂电机最大转矩，pem为轮毂电机转矩为零时的损失功率。

40、根据汽车需求总的力、力矩和行驶约束设置目标函数实现的约束条件，通过matlab软件编程进行最优求解，获得各个轮毂电机的转矩。

41、与现有技术相比，本发明具有如下优点：

42、采用本发明的方案，四轮毂电机驱动智能汽车在行驶过程中，各轮毂电机转矩的合理分配不仅可以减少能量的损耗，还可以保证汽车稳定行驶。本发明选择汽车质心侧偏角及其角速度两个特征量，利用汽车二自由度非线性动力学模型，输入汽车质心侧偏角和横摆角速度的初始值，构建汽车质心侧偏角-侧偏角速度的相平面，确定汽车稳定行驶区域和可拓集合，基于可拓控制理论确定汽车基于稳定性和节能的轮毂电机转矩分配控制目标函数的动态权重系数，实时动态分配轮毂电机转矩，兼顾整车的行驶稳定性和经济性。