一种基于H∞控制的车队协同式自适应巡航控制方法

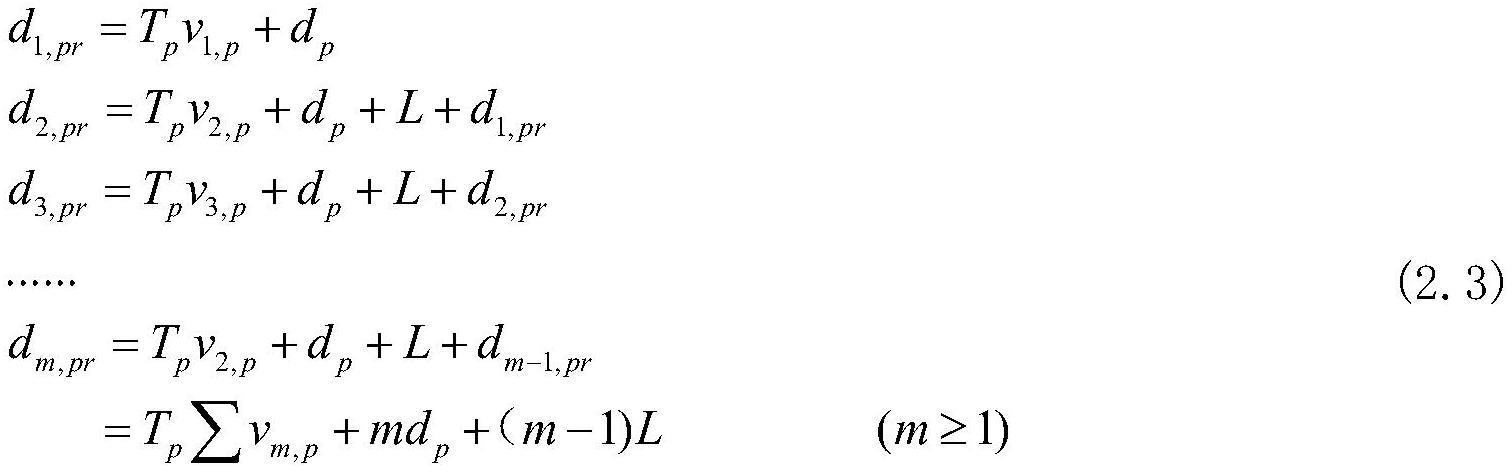
本发明属于智能驾驶，具体涉及一种基于h∞控制的车队协同式自适应巡航控制方法。

背景技术：

1、cacc系统的鲁棒控制问题。底盘系统建模误差、底盘系统参数不确定性和前方车辆加速度扰动均是cacc系统控制中无法忽略的扰动问题，但目前研究对这些扰动的综合考虑较少，建立提高系统稳定性的鲁棒控制器是cacc系统控制的核心问题。目前常用的cacc控制算法包括lqr控制、pid控制、模糊控制、模型预测控制、滑模控制等。由于lqr控制是一种仅限于线性系统的控制方法，因此需要将系统进行线性化，而线性化后的系统无法保证模型精度，对车辆稳定性控制影响非常大。pid控制虽然简单，控制效果也尚可，但是无法添加系统约束，较难适应多输入多输出且强耦合的系统。模糊控制系统灵活简单，对非线性问题的处理有独特优势，但是模糊控制对周围行驶的高速车辆检测信息不准确，导致实际控制效果不佳。模型预测控制虽然可以实现对指标和系统约束的双重设计，但约束条件增加的同时也增加了求解难度。滑模控制响应速度快，且易于物理实现，但是应用中需要在不同的控制中进行不同的切换以保证系统的持续运动，导致系统容易出现高频抖动问题，且难以抑制。

2、只有合理优越的控制方法才能保证车队一致性，使驾驶舒适性、燃油经济性和行车安全性得到保证。目前研究对cacc系统控制的鲁棒性考虑较少，然而底盘系统建模误差、底盘系统参数不确定性和前方车辆加速度扰动均是影响cacc系统稳定性的重要因素，因此对cacc系统控制过程中应加强鲁棒控制的考虑。

3、此外，现有的研究对车队中前方车辆的信息使用非常有限，大多数研究仅限于使用距离本车最近的前车速度信息和位置信息，然而对于前方其他车辆的信息基本没有涉及，无法充分发挥车间通信的优势。如，专利cn114394092a公布了一种基于车车通信的混合车流汽车协同自适应巡航控制方法，步骤如下：实时采集车辆跟驰过程中首车(人工驾驶汽车)、前车(自动驾驶汽车)与本车(自动驾驶汽车)的bsm信息集，并基于bsm信息集建立相邻两车的跟驰运动模型；利用线性最优二次理论建立首车扰动工况下前车驾驶操纵效用函数，预测下一时刻前车加速度值；将下一时刻前车加速度值代入跟驰运动模型中，得到本车加速度的预测值，将预测值与期望值进行比较得到本车最优控制序列，根据本车最优控制序列对车辆编队自适应巡航滚动控制。其存在以下缺点，(1)该策论虽然采用了车辆之间通讯的方式来获取前车的信息，但对前车信息使用非常有限，对车队中其他车辆的信息基本没有涉及，并没有充分发挥车间通讯的优势。(2)该策略采用的模型预测控制算法计算量较大，在预测过程中，需要进行优化求解，因此需要较强的计算资源，运行成本较高，且实时性不高，难以在实车上应用。(3)该策略没有考虑车辆底盘系统建模误差、底盘系统参数不确定性和前方车辆加速度扰动对车队cacc的舒适性、跟驰性能的影响，对cacc系统控制的鲁棒性考虑较少。

4、基于此，将对如何合理使用前方一定范围内车辆的信息展开研究。旨在充分利用车间通讯的优势，且提高车辆的跟车性能、舒适性和安全性能。

技术实现思路

1、本发明要解决的技术问题是提供一种基于h∞控制的车队协同式自适应巡航控制方法，以车队的纵向控制为研究对象，针对车队控制中的一致性问题以及鲁棒性问题展开研究。考虑车辆底盘系统建模误差、底盘系统参数不确定性，利用车辆运动学对协同自适应巡航系统建模，对协同自适应巡航系统的干扰项分析处理，构造闭环控制系统。提出一种将领导车辆作为跟车目标的车队结构。选取被控车辆与领导车辆之间的跟车距离误差、速度误差和被控车辆的加速度作为系统状态，对所提出的车队cacc系统进行数学建模。对于系统中的扰动问题，利用李雅普诺夫稳定性理论建立反馈增益解算的h∞控制准则。以此满足车队控制的一致性、鲁棒性、跟车性能和舒适性要求。

2、为解决上述问题，本发明采用如下技术方案：

3、一种基于h∞控制的车队协同式自适应巡航控制方法，该方法包括以下步骤：

4、p1：考虑底盘系统建模误差、底盘系统参数不确定性以及目标车辆加速度的扰动对系统稳定性的影响；首先对被控车辆的底盘系统进行简化处理，使用一阶惯性环节对其建模：

5、

6、其中，aego表示本车的实际加速度，ar表示本车的期望加速度；

7、底盘系统时间τ一般作为常数处理，但受到底盘系统不确定性的影响会有一定的偏差，因此实际底盘系统时间τa＝τ+δτ；其中，δτ表示底盘系统不确定性引起的有界系统干扰，且|δτ|≤δmax；

8、根据一阶泰勒展开式：

9、

10、考虑底盘系统建模误差和底盘系统参数不确定性的影响，车辆底盘系统模型为：

11、

12、其中，ωτ2为由底盘系统参数不确定性引入的不确定性项，

13、考虑底盘系统建模误差及底盘系统参数不确定性，进一步对车辆底盘系统进行建模：

14、

15、其中，ωτ1表示底盘系统建模误差，ωτ表示由底盘系统建模误差和底盘系统参数不确定性共同引起的不确定性项，ωτ＝ωτ1+ωτ2；

16、p2：根据车队cacc系统，基于跟车结构对车队cacc系统状态进行设计，选取以领导车辆为跟车目标的跟车距离误差、跟车速度误差和被控车辆的加速度作为车队cacc系统状态；旨在使得被控车辆与领导车辆的实际距离与期望距离的误差尽可能小，被控车辆的车速尽可能跟踪领导车辆的车速，从而保证跟车性能；被控车辆的加速度尽可能小，以保证舒适性；同时减小跟车的延迟性；

17、(1)跟车距离误差：

18、被控车辆与领导车辆的距离dm,p为：

19、dm,p＝p0,p-pm,p-l                           (2.1)

20、其中，p0,p和pm,p分别表示在车队cacc系统中领导车辆和第m辆车的位置，l表示车辆的长度；

21、将车队cacc系统中第m辆车距离领导车辆的实际距离与期望距离的差值定义为跟车距离误差，则跟车距离误差可表示为：

22、dm,p＝dm,p-dm,pr                   (2.2)

23、车队中所有车辆的期望跟车距离均是基于领导车辆进行设计，其计算公式可以表示为：

24、

25、其中，dm,p表示第m辆车与领导车辆的期望跟车距离，tp表示跟车时距，此处取值为1.1s；dp表示与前车的最小跟车距离；vm,p表示第m辆车的车速；从公式2.3中可以看出，每辆跟随车辆都对领导车辆进行跟踪，每辆车的期望跟车距离与本车到领导车辆之间所有车辆都有关；

26、对公式2.3进行求导得：

27、

28、其中，v0,p表示领导车辆的车速，am,p表示第m辆被控车辆的加速度；

29、(2)跟车速度误差

30、将领导车辆与第m辆跟随车辆的速度差值定义为跟车速度误差vm,pe，领导车辆的车速可以通过车间通信获取，则跟车速度误差可以表示为：

31、vm,pe＝v0,p-vm,p                             (2.5)

32、对公式2.5求导可得：

33、

34、p3：车队cacc系统建模:

35、选取跟车距离误差dm,pe、跟车速度误差vm,pe和被控车辆的加速度am,p作为车队cacc系统状态，将期望加速度am,pr作为系统输入，并考虑底盘系统建模误差和底盘系统参数不确定性的影响，联合公式2.4、公式2.6和底盘模型对车队cacc系统建模得：

36、

37、车队cacc系统的状态空间描述为：

38、

39、其中，xm,p＝[dm,pe,vm,pe,am,p]t，b1,p＝[0,0,1/τ]t,um,p＝am,pr表示第m辆被控制的期望加速度；

40、p4:建立以领导车辆为跟踪目标的车队cacc系统，考虑到车队cacc系统稳定性较差，利用李雅普诺夫稳定性理论设计状态反馈控制器；设计基于h∞控制的车队cacc系统控制器，首先对车队cacc系统能控性进行分析，从公式(3.2)可以看出车队cacc系统是一个线性定常系统，构造能控性矩阵为：

41、

42、能控性矩阵的行列式为：

43、

44、在公式(4.2)中，τ≠0，说明|wp|≠0，能控性矩阵wp为满秩矩阵，因此车队cacc系统可控；此外车队cacc系统中的状态均可测，因此设计车队cacc系统的状态反馈控制器：

45、um,p＝-kpxm,p                     (4.3)

46、其中，kp为车队cacc系统闭环控制状态反馈控制器的增益矩阵；

47、则，车队cacc系统闭环控制的状态空间描述为：

48、

49、其中，ac,p表示闭环系统矩阵，ac,p＝ap-b1,pkp；

50、根据式4.4可知，即使车队cacc系统使用状态反馈控制进行系统控制，但是仍有ωm,p作为车队cacc系统的扰动项影响系统的稳定性；需要使用抗干扰能力极强的h∞控制方法对车队cacc系统进行控制；

51、给定常数γp＞0，存在正定对称矩阵pp,inv和矩阵qp，且满足以下线性矩阵不等式，则车队cacc系统具有h∞性能：

52、

53、利用李雅普诺夫稳定性理论证明车队cacc系统闭环控制具有如下h∞性能：

54、

55、其中矩阵qp＝kppinv,p，利用matlab中的lmi工具箱可获得状态反馈增益，求解出kp＝[-0.335 -0.542 0.152]；

56、p5：为验证本文提出控制方法的有效性，以德国dspace公司生产的dspace实时系统作为控制平台进行测试，其优点在于可以和matlab/simulink模型完美对接，方便实现代码的编译、下载和调试。dspace实时系统主要包括软件部分和硬件部分：上位机软件controldesk和microautobox控制器。controldesk主要用于对模型中的参数进行实时调试，对仿真数据进行观测、存储等，将控制算法模型以sdf文件的形式通过以太网通信加载到microautobox控制器中。microautobox控制器可为实验测试平台提供良好的计算性能，其拥有丰富的输入输出接口，本文主要用到can通信接口和以太网通信接口，并配有12v电源接口。

57、在步骤p1中，针对底盘系统建模误差、底盘系统参数不确定性是影响车队cacc系统稳定性的重要因素，为了提高系统的稳定性，在对车辆底盘系统建模时加入底盘系统建模误差、底盘系统参数不确定性因素，提高车队cacc系统的稳定性。

58、在步骤p2中，首先车队中车辆的acc配置情况、通信情况和车辆的编号情况与传统cacc保持一致。不同的是每辆跟随车辆都对领导车辆进行跟踪，每辆车的期望跟车距离与本车到领导车辆之间所有车辆都有关。而传统cacc的跟车目标是距离被控车辆最近的前车。车队cacc可以充分发挥车间通信的优势，在速度跟踪问题上合理利用领导车辆的信息，在距离跟踪问题上充分利用行驶车道内本车到领导车辆之间全部车辆的信息。

59、具体的跟车距离误差：

60、车队中第一辆车由驾驶人员操作即领导车辆，之后车队的每一辆车都配备acc和车队cacc功能，每辆车都以领导车辆为跟车目标。即期望的跟车距离为前方车辆与领导车辆跟车距离加前车车辆的车身长度和期望的与前车车辆的安全车距之和即为理想的跟车距离误差。

61、跟车速度误差和跟车加速度误差:

62、将领导车辆与第m辆跟随车辆的速度差值定义为跟车速度误差领导车辆的车速可以通过车间通信获取，跟车加速度误差为am,p。

63、在步骤p3中，加入底盘系统建模误差、底盘系统参数不确定性因素的影响，选取p2中的跟车距离误差、跟车速度误差和本车的加速度作为系统状态，对cacc系统建模，在系统鲁棒性、跟车性能和舒适性均取得了较好的效果。

64、在步骤p4中，针对cacc系统建模，利用李雅普诺夫稳定性理论设计状态反馈控制器；接下来，考虑到系统扰动，设计h∞控制策略。采用基于h∞控制的车队cacc。旨在使得被控车辆与领导车辆的实际距离与期望距离的误差尽可能小，被控车辆的车速尽可能跟踪领导车辆的车速，从而保证跟车性能；被控车辆的加速度尽可能小，以保证车队一致性、跟车性能和舒适性。

65、具体的李雅普诺夫稳定性理论设计状态反馈控制器过程：

66、证明：李雅普诺夫函数被设计为：

67、v(x)＝xm,ptppxm,p                    (4.7)

68、李雅普诺夫函数的导数为：

69、

70、考虑到系统中的噪声，为了保证系统h∞性能，评价指标j1被引进：

71、

72、根据schur补定理，评价指标j1可以被等价描述为j2：

73、

74、设pinv,p＝pp-1，则评价指标函数j2可表示为j3：

75、

76、将ac,p＝ap-b1,pkp，qp＝kppinv,p带入到公式j3中可得：

77、

78、经上述推导可知，j3＜0等价于j1＜0，即只要保证不等式j3＜0成立，则j1＜0成立。给定正标量γ＞0，如果存在正定对称矩阵pinv,p和矩阵qp，使得j3＜0成立，则j1＜0，两边进行积分可得：

79、根据李雅普诺夫稳定性定义可知:

80、

81、将李雅普诺夫函数带入到(4.14)可得:

82、

83、由于xm,pt(t)ppxm,p(t)＞0，pp≤λp,max(pp)i，可得:

84、

85、根可4.16，4.13表示为：

86、

87、证毕；

88、给定正标量λp>0，求解出pinv,p和矩阵qp，使得j3＜0成立，式4.5的闭环系统的控制器增益为kp＝qppp，则式4.5的闭环系统具有式4.6的h∞性能。