一种基于非线性MPC快速求解方法的纵向自适应控制方法与流程

本发明涉及速度规划领域，特别涉及一种基于非线性mpc快速求解方法的纵向自适应控制方法。

背景技术：

1、汽车自适应巡航控制(adaptive cruise control，acc)系统关注汽车安全性、舒适性及快速性等多方面因素，目前有基于pid控制、模糊控制、滑模控制、最优控制以及模型预测控制等控制理论的acc系统控制策略。

2、实际工程问题中，线性控制方法不能很好的描述系统，可以用非线性模型对系统进行描述。在此背景下，非线性模型预测控制(nonlinear model predictive control，nmpc)被引入工程系统当中，处理复杂的问题。在模型预测控制的框架下，将汽车自适应巡航控制算法设计转化为带约束的在线二次优化问题。

3、理论上连续系统的最优控制问题主要有两类数值求解方法：直接法和间接法。根据直接法的原理可知，无论选用何种数值迭代方法(如序列二次规划，内点法等)，都需要求解一个非线性规划(nonlinear programming,nlp)问题。当求解nlp问题时，直接法将预测时域内离散的状态变量x(1),x(2),...,x(np)和控制变量u(1),u(2),...,u(nc)作为独立变量进行求解，所以问题的维度随着预测步数np的增加而增加，而这将导致问题的复杂度和求解时间指数增长。因此，对于预测时域较长的模型预测控制问题，直接法的计算量会大幅上升。

4、不同于直接法，间接方法通过求解最优控制问题的必要性条件找到原始问题的最优解(或次优解)。例如通过使用极值原理将非线性优化控制问题转化为一个非线性方程组的求解问题，最终实现快速求解。间接法的主要思想是通过内点法，牛顿法等寻找满足最优必要性条件的协态变量初始值，并以此确定最优控制变量。

5、虽然nmpc具有处理约束和实时优化的能力，通过直接法求解，或者依赖于市面上成熟的二次规划求解器求解，计算过程很复杂，对控制器性能提出更高要求，目前较少有文献表明在低成本硬件方案中实现了nmpc方法的实车应用。有研究通过间接法求解nmpc，应用于车辆的节能巡航控制，该方案的控制对象为发动机控制单元和制动系统控制单元，分别控制车辆的扭矩和制动。对于市面上控制对象是速度控制单元(velocity longitudinalcontrol)，目前还没有相关nmpc的应用研究。

技术实现思路

1、本发明的目的是克服现有技术缺陷，提供一种基于非线性mpc快速求解方法的纵向自适应控制方法，针对长时域预测的非线性模型预测控制问题计算量大、难以在实际工程中应用的问题，提出了基于车辆运动学特性的长时域非线性mpc快速求解方法；通过引入协态变量将非线性优化问题转化为两点边值问题，利用被控系统的特性获得协态变量初值下最优控制序列的解析表达，降低了优化控制问题的维度和复杂度。

2、本发明的目的是这样实现的：一种基于非线性mpc快速求解方法的纵向自适应控制方法，具体包括以下步骤：

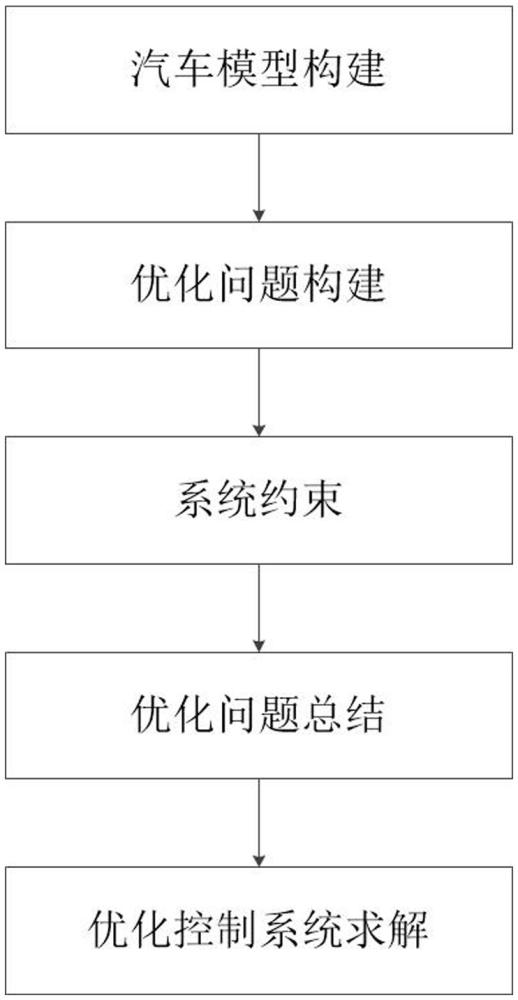
3、1)汽车系统模型构建，车辆纵向运动学模型简化为单自由度模型；

4、2)优化问题构建，选定预测时域内的速度跟踪性为目标函数，在速度跟踪项基础上增加惩罚项，并构建代价函数；

5、3)系统约束，将系统的状态量和控制量约束在一定范围内，包括速度约束，加速度约束和加加速度约束；

6、4)通过综合控制优化代价函数以及对应的约束条件，得到相应的优化函数；

7、5)优化控制系统求解，引入哈密顿函数，通过给定当前车速和目标信息求得一元二次方程的值和显性解，求得输出控制量为加速度，并将其应用于速度控制单元。

8、作为本发明的进一步限定，所述步骤1)中所述车辆纵向运动学模型通过车辆行驶距离s(k)、车辆行驶速度v(k)和车辆纵向加速度a(k)来描述，具体如式(1)和式(2)所示：

9、

10、

11、作为本发明的进一步限定，步骤2)中所述构建代价函数为：

12、

13、其中，目标函数l[x(k),u(k),k]定义为：

14、l[x(k),u(k),k]＝k1*(v(k)-vd)2*δt+k2*(a(k)-a(k-1))2*δt (4)

15、终端约束定义为：

16、

17、其中，n为预测时域对应的离散点数，vd为驾驶任务中的参考车速，k1为速度跟踪性权重系数，k2为加速度跟踪性权重系数，k3为终端速度约束权重系数；(v(k)-vd)2为速度跟踪性指标；(a(k)-a(k-1))2为加速度跟踪性指标；(v(n)-vd)2为保终端惩罚性指标。

18、作为本发明的进一步限定，步骤3)中所述车速约束具体包括：对于状态变量应该满足的速度约束为：

19、vmin≤ v(k)≤vmax                  (6)

20、其中，vmin是车速允许最小值，vmax是车速允许最大值，根据实际驾驶场景，vmin＝0kph，vmax＝90kph；

21、所述加速度约束具体包括：车辆能提供的加速度和减速度有一定范围，因此对自适应巡航控制系统的加速度约束为：

22、amin≤ v(k)≤amax                 (7)

23、amax为最高响应加速度，amin为最小响应制动加速度；

24、所述加加速度约束具体包括：对车辆的加加速度做一定的限制，因此对自适应巡航控制系统的加加速度约束为：

25、jerkmin≤ jerk(k)≤jerkmax             (8)

26、jerkmax为最大响应加加速度，jerkmin为最小响应加加速度。

27、作为本发明的进一步限定，所述步骤4)具体包括：通过综合控制优化代价函数以及对应的约束条件，控制器的优化问题总结为如下形式：

28、

29、

30、系统控制变量为加速度，即u(k)＝[a(k)]t，系统状态变量为车辆位移和速度，即x(k)＝[s(k)v(k)]t。

31、作为本发明的进一步限定，所述步骤5)具体包括：根据优化问题最优必要性条件，哈密顿函数由下式定义：

32、h(k)＝h(x(k),u(k),λ(k+1),k)

33、＝l[x(k),u(k),k]+λ1(k+1)*v(k)*δt+λ2(k+1)*a(k)*δt  (11)

34、将(4)式代入到(11)式中，进一步整理得到关于控制变量a(k)或状态变量v(k)的二次多项式形式：

35、h(k)＝p1(k)a(k)2+p2(k)a(k)+p3(k)

36、＝p4(k)v(k)2+p5(k)v(k)+p6(k)       (12)

37、哈密顿函数h(k)整理为关于a(k)的一元二次多项式方程：二次项系数p1(k)关于k2、δt的函数，为方程中a(k)2的系数；一次项系数p2(k)关于λ2(k+1)、k2、δt、a(k-1)的函数，为方程中的a(k)系数；常数项p3(k)关于v(k)、k1、k2、δt、a(k-1)的函数，为方程中的常数，表示没有包含a(k)项的数字；二次项系数p4(k)关于k2、δt的函数，为方程中v(k)2的系数；一次项系数p5(k)关于k1、δt的函数，为方程中的v(k)系数；常数项p6(k)关于λ2(k+1)、k3、δt、a(k-1)的函数，为方程中的常数，表示没有包含v(k)项的数字；

38、根据庞德里亚金极小值原理，最优状态变量x*(0)，最优控制输入u*(0)和对应的协态变量λ*(k+1)＝[λ1(k+1)λ2(k+1)]t必须使哈密顿函数取得最小值：

39、h(x*(k),u*(k),λ*(k+1),k)＝minu(k)∈ωh(x*(k),u(k),λ*(k+1),k)  (13)

40、协态变量的迭代方程为：

41、

42、

43、协态变量的边界条件为：

44、

45、

46、由于哈密顿函数h(k)中不包含路程s(k)，因此：

47、λ1(k)≡0(18)

48、进一步整理得到：

49、p1(k)＝k2*δt

50、p2(k)＝λ2(k+1)*δt-2*k2*a(k-1)*δt

51、p3(k)＝k1(v(k)-vd)2*δt+k2*a(k-1)2*δt

52、p4(k)＝k2*δt

53、p5(k)＝-2*k1*vd*δt

54、p6(k)＝k3(a(k)-a(k-1))2*δt+λ2(k+1)*a(k)*δt+k1*δt*vd2

55、其中，哈密顿函数在每个预测步数迭代求解过程中，车辆状态需要根据车辆运动学模型进行实时更新。

56、本发明采用以上技术方案，与现有技术相比，有益效果为：本方法使用极值原理将原始最优控制问题转化为关于加速度的一元二次方程根的求解问题；将nmpc应用到低成本硬件系统方案中，控制输出量为加速度，适用于驱动接口为加速度的控制器；通过引入协态变量将非线性优化问题转化为两点边值问题，利用被控系统的特性获得协态变量初值下最优控制序列的解析表达，降低了优化控制问题的维度和复杂度；同时，在求解两点边值问题时，引入了填充函数法以得到协态变量初值的全局最优解。最后将该方法应用于汽车速度规划优化问题中，并取得良好效果。