一种汽车转向轮前束变化确定的三维造型方法与流程

本发明涉及汽车技术领域，具体而言，涉及一种汽车转向轮前束变化确定的三维造型方法。

背景技术：

汽车转向轮前束的变化直接影响车辆的操纵稳定性和舒适性，也影响车辆在弯道中的行驶特性。在汽车的实际开发过程中，为满足车辆操纵稳定性的要求，势必需确认汽车转向轮前束的变化。目前可通过作图法、函数法、cae软件法等方法进行汽车转向轮前束变化的确定。作图法是根据画法几何理论在图纸上模拟载荷变化、前束变化，其直观性强，但是精度差，效率低。函数法是建立转向轮前束计算的数学模型，代入初始条件计算。此方法精度高，但是建模费时，效率低，易出错。cae软件法是利用cae软件代入初始条件进行自动计算。此方法精度高，但是学习cae软件费时，直观性差，易出错。

技术实现要素：

本发明提供了一种汽车转向轮前束变化确定的三维造型方法，旨在改善汽车转向轮前束变化确定费时、效率低的问题。

本发明是这样实现的：

一种汽车转向轮前束变化确定的三维造型方法，包括如下步骤：

s1：建立转向系统结构模型；

利用绘图工具按照比例绘制转向系统结构模型，设计并表达转向系统零件几何形状、尺寸、位置和相互连接关系；转向系统包括转向拉杆和转向节，转向拉杆与转向节连接；

s2：建立满载工况转向拉杆-转向节几何模型；

在转向系统结构模型基础上绘制满载工况下转向拉杆-转向节投影三视图，反映转向拉杆与转向节之间几何连接关系，即转向系统的转向拉杆至转向节传动段；

s3：建立转向节的转动锥面轨迹三维模型；

在满载工况的基础上，模拟转向节随载荷变化的运动规律，转向节的运动轨迹构成锥面，构建转向节的转动锥面轨迹三维模型；

s4：建立转向拉杆的转动球面三维模型；

在满载工况的基础上，模拟转向拉杆随载荷变化的运动规律，转向拉杆的运动轨迹构成球体，构建转向拉杆的转动球面三维模型；

s5：建立满载工况下，转向节与转向拉杆的交点计算三维模型；

利用绘图工具在同一坐标系下建立转向节的转动锥面轨迹三维模型以及转向拉杆的转动球面三维模型，构建转向节与转向拉杆的交点计算三维模型，用于获得转向节与转向拉杆交点的位置；

s6：确定加载或减载工况下，转向节与转向拉杆的交点位置；

在转向系统载荷改变时，根据转向节与转向拉杆的交点计算三维模型，获得加载或减载工况下，转向节与转向拉杆的交点位置；

s7：确定转向轮前束变化；

在转向系统载荷改变时，转向节与转向拉杆几何模型发生改变，通过测量转向系统载荷变化前后转向节的转动角度获得转向轮前束变化。

进一步地，在本发明较佳的实施例中，s1步骤中，绘图工具为autocad软件。

进一步地，在本发明较佳的实施例中，s2步骤中，在采用autocad软件建立转向系统平面模型后，结合画法几何理论，模拟载荷变化时转向拉杆-转向节传动段运动规律。

进一步地，在本发明较佳的实施例中，s2步骤中，转向拉杆-转向节几何模型包括第一端点、第二端点和第三端点，第一端点表示转向拉杆内端球铰中心，第二端点表示转向拉杆外端球铰中心，且为转向拉杆与转向节的交点，第三端点表示汽车转向轮中心线与转向轮主销中心线的交点。第一端点和第二端点连接构成第一投影线，第一投影线用于表示转向拉杆，第二端点与第三端点连接构成第二投影线，第二投影线用于表示转向节。

进一步地，在本发明较佳的实施例中，s3步骤中，不考虑转向拉杆的联接，模拟第二投影线上的第二端点的运动，以第三端点为顶点，第二投影线绕转向轮主销中心线转动形成转向节的转动锥面，第二端点的回转平面形成转动锥面的底面，随载荷变化，第二端点的运动轨迹被约束在回转平面的圆周上。

进一步地，在本发明较佳的实施例中，在满载工况基础上，根据转向节的转动锥面轨迹三维模型，采用画法几何投影法求出第三端点到回转平面的距离以及回转平面的半径。

进一步地，在本发明较佳的实施例中，s4步骤中，不考虑转向节的联接，模拟第一投影线上第二端点的运动，以第一端点为球心，第一投影线绕第一端点转动形成球体，随载荷变化，第二端点的运动轨迹被约束在球体的球面上。

进一步地，在本发明较佳的实施例中，转向系统包括方向盘传动管柱、方向盘、方向盘管柱、花键转换器、方向机、方向机齿条拉杆、右转向节摇臂、右转向拉杆、右转向节、转向横拉杆、左转向节、左转向拉杆、左转向节摇臂。

方向盘安装在方向盘管柱的一端，方向盘管柱的远离方向盘的一端依次连接有方向盘传动管柱、花键转换器、方向机、方向机齿条拉杆、右转向节摇臂。

转向横拉杆的两端分别与右转向拉杆和左转向拉杆连接，右转向拉杆远离转向横拉杆的一端连接右转向节，右转向节连接至汽车的右转向轮，左转向拉杆远离转向横拉杆的一端与左转向节连接，左转向节连接至汽车的左转向轮。

当方向机齿条拉杆带动右转向节摇臂转动时，转向横拉杆带动右转向拉杆和左转向拉杆转动，右转向拉杆带动右转向节和右转向轮一起转动，左转向拉杆带动左转向节和左转向轮一起转动。

左转向轮和右转向轮在回转中心分别具有主销轴线，在左转向轮和右转向轮转向时，左转向轮和右转向轮以各自的主销轴线为轴线向左、右转动。

转向轮前束为右转向轮和左转向轮之间的夹角，随汽车载荷变化，左转向拉杆和右转向拉杆两端点运动不一致，导致左转向轮和右转向轮之间夹角改变，左转向轮和右转向轮之间夹角的变化体现转向轮前束的变化。

进一步地，在本发明较佳的实施例中，右转向摇臂、右转向节和转向横拉杆之间均通过球销连接，左转向摇臂、左转向节和转向横拉杆之间均通过球销连接。

进一步地，在本发明较佳的实施例中，在转向系统载荷改变时，根据转向节与转向拉杆的交点计算三维模型获得右转向节载荷变化前后的右转向节与右转向拉杆的交点位置，再根据转向拉杆-转向节几何模型获得右转向节载荷变化前后的转动角度，转向轮前束变化为2倍右转向节的转动角度。

本发明的有益效果是：

本发明采用autocad软件建立转向系统结构模型，结合画法几何理论，模拟载荷变化时转向拉杆-转向节传动段运动规律，通过模拟转向拉杆和转向节运动分别建立满足转向拉杆外端球铰中心绕主销中心线转动条件的三维锥面模型，同时建立满足转向拉杆外端球铰中心绕转动拉杆内端球铰中心转动条件的三维球面模型，获得转向拉杆外端球铰中心的计算三维模型，为前束变化角的确定奠定基础。通过该方法能够准备方便地确定转向拉杆外端球铰中心的位置，从而通过转向拉杆-转向节几何模型确定转向节载荷变化前后的夹角，确定前束变化，直观性好，效率高和精度高。利用画法几何方法确定锥面三维模型和球面三维模型形状尺寸，有利于提高三维模型建模效率。

附图说明

为了更清楚地说明本发明实施方式的技术方案，下面将对实施方式中所需要使用的附图作简单地介绍，应当理解，以下附图仅示出了本发明的某些实施例，因此不应被看作是对范围的限定，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他相关的附图。

图1是本发明实施例汽车转向系统结构主视图；

图2是本发明实施例汽车转向系统结构的左视图；

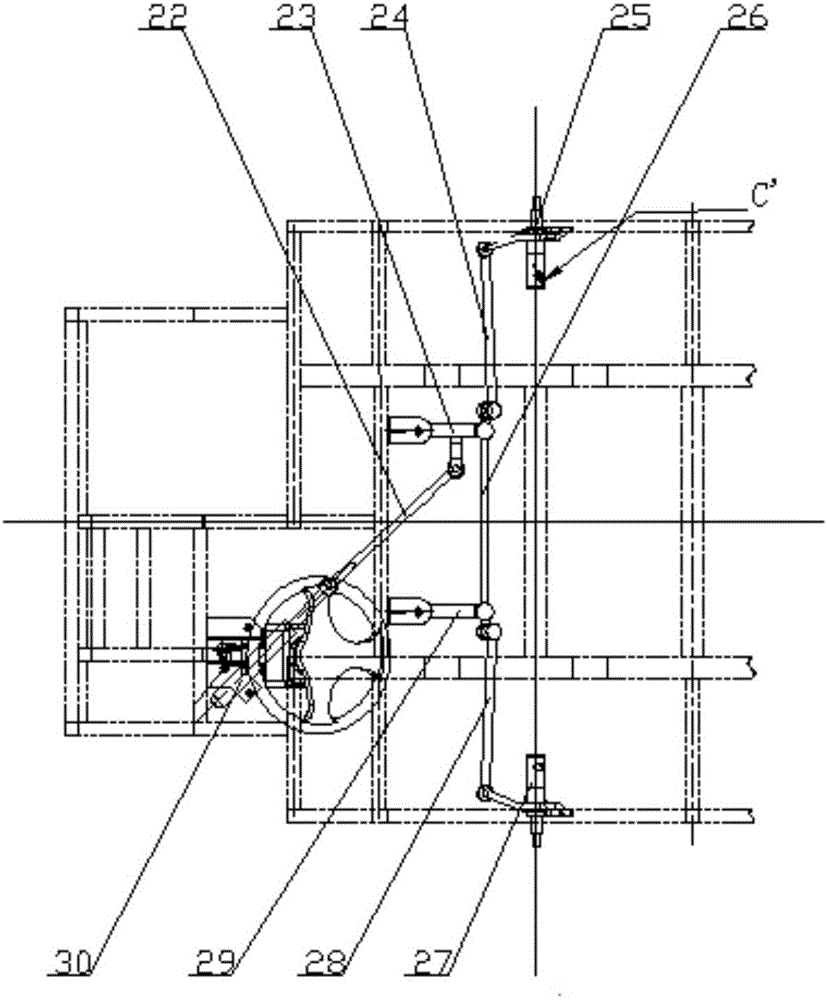
图3是本发明实施例汽车转向系统结构的俯视图；

图4是本发明实施例满载工况右转向拉杆-转向节几何模型主视图；

图5是本发明实施例满载工况右转向拉杆-转向节几何模型左视图；

图6是本发明实施例满载工况右转向拉杆-转向节几何模型俯视图；

图7是本发明实施例右转向节转动锥面轨迹三维模型图；

图8是本发明实施例右转向拉杆转动球面轨迹三维模型图；

图9是本发明实施例中转向拉杆外端球铰中心计算三维模型；

图10是本发明实施例右转向拉杆-转向节几何模型俯视图。

图标：1-方向盘传动管柱；2-管柱锁紧螺母；3-方向盘托架；8-方向盘；10-锁芯；11-方向盘管柱壳；12-方向盘管柱；13-管柱锁紧螺母；14-花键转换器；15-方向机齿条拉杆销；16-齿条拉杆螺母；18-转向摇臂支架销；19-摇臂支架销螺母；20-球销；21-转向节摇臂支架；22-方向机齿条拉杆；23-右转向节摇臂；24-右转向拉杆；25-右转向节；26-转向横拉杆；27-左转向节；28-左转向拉杆；29-左转向节摇臂；30-方向机支架。

具体实施方式

为使本发明实施方式的目的、技术方案和优点更加清楚，下面将结合本发明实施方式中的附图，对本发明实施方式中的技术方案进行清楚、完整地描述，显然，所描述的实施方式是本发明一部分实施方式，而不是全部的实施方式。基于本发明中的实施方式，本领域普通技术人员在没有作出创造性劳动前提下所获得的所有其他实施方式，都属于本发明保护的范围。因此，以下对在附图中提供的本发明的实施方式的详细描述并非旨在限制要求保护的本发明的范围，而是仅仅表示本发明的选定实施方式。基于本发明中的实施方式，本领域普通技术人员在没有作出创造性劳动前提下所获得的所有其他实施方式，都属于本发明保护的范围。

在本发明的描述中，需要理解的是，术语“中心”、“纵向”、“横向”、“长度”、“宽度”、“厚度”、“上”、“下”、“前”、“后”、“左”、“右”、“竖直”、“水平”、“顶”、“底”、“内”、“外”、“顺时针”、“逆时针”等指示的方位或位置关系为基于附图所示的方位或位置关系，仅是为了便于描述本发明和简化描述，而不是指示或暗示所指的设备或元件必须具有特定的方位、以特定的方位构造和操作，因此不能理解为对本发明的限制。

此外，术语“第一”、“第二”仅用于描述目的，而不能理解为指示或暗示相对重要性或者隐含指明所指示的技术特征的数量。由此，限定有“第一”、“第二”的特征可以明示或者隐含地包括一个或者更多个该特征。在本发明的描述中，“多个”的含义是两个或两个以上，除非另有明确具体的限定。

在本发明中，除非另有明确的规定和限定，术语“安装”、“相连”、“连接”、“固定”等术语应做广义理解，例如，可以是固定连接，也可以是可拆卸连接，或成一体；可以是机械连接，也可以是电连接；可以是直接相连，也可以通过中间媒介间接相连，可以是两个元件内部的连通或两个元件的相互作用关系。对于本领域的普通技术人员而言，可以根据具体情况理解上述术语在本发明中的具体含义。

在本发明中，除非另有明确的规定和限定，第一特征在第二特征之“上”或之“下”可以包括第一和第二特征直接接触，也可以包括第一和第二特征不是直接接触而是通过它们之间的另外的特征接触。而且，第一特征在第二特征“之上”、“上方”和“上面”包括第一特征在第二特征正上方和斜上方，或仅仅表示第一特征水平高度高于第二特征。第一特征在第二特征“之下”、“下方”和“下面”包括第一特征在第二特征正下方和斜下方，或仅仅表示第一特征水平高度小于第二特征。

实施例1

本发明实施例提供一种汽车转向轮前束变化确定的三维造型方法，包括如下步骤：

s1：建立转向系统结构模型；

利用绘图工具按照比例绘制转向系统结构模型，设计并表达转向系统零件几何形状、尺寸、位置和相互连接关系；转向系统包括转向拉杆和转向节，转向拉杆与转向节连接。

请参照图1-3，汽车转向系统结构包括：方向盘传动管柱1、方向盘托架3、方向盘8、方向盘管柱12、花键转换器14、方向机、方向机齿条拉杆22、球销20、右转向节摇臂23、右转向拉杆25、右转向节25、转向横拉杆26、左转向节27、左转向拉杆28、左转向节摇臂29；

方向盘8安装在方向盘管柱12的端部，方向盘管柱12连接在方向盘托架3上，锁芯10安装在方向盘管柱12上，用于固定控制方向盘管柱12，方向盘管柱壳11包覆在方向盘管柱12的外侧，用于对方向盘管柱12形成保护。

方向盘管柱12远离方向盘8的一端依次连接有方向盘传动管柱1、花键转换器14、方向机、方向机齿条拉杆22、右转向节摇臂23。具体地，方向盘传动管柱1通过管柱锁紧螺母13与花键转换器14相连。花键转换器14通过方向机与方向机齿条拉杆22相连，方向机齿条拉杆22通过方向机齿条拉杆销15、齿条拉杆螺母16连接至右转向节摇臂23。右转向节摇臂23和左转向节摇臂29分别安装在转向节摇臂支架21上，并可围绕转向节摇臂支架21转动，转向节摇臂支架21固定连接在车架上，方向机齿条拉杆22能带动右转向节摇臂23和左转向节摇臂29一起旋转。

右转向节摇臂23和左转向节摇臂29分别连接至转向横拉杆26，转向横拉杆26的两端分别通过球销20与右转向拉杆24和左转向拉杆28连接。右转向拉杆24远离转向横拉杆26的一端通过球销与右转向节25连接，右转向节25连接至汽车的右转向轮。左转向拉杆28远离转向横拉杆26的一端通过球销20与左转向节27连接，左转向节27连接至汽车的左转向轮。

当方向机齿条拉杆22带动右转向节摇臂23转动时，转向横拉杆26带动右转向拉杆24和左转向拉杆28转动，右转向拉杆24带动右转向节25和右转向轮一起转动，左转向拉杆28带动左转向节27和左转向轮一起转动。

左转向轮和右转向轮在回转中心分别具有主销轴线c’，在左转向轮和右转向轮转向时，左转向轮和右转向轮以各自的主销轴线c’为轴线向左、右转动。

汽车转向系统工作过程如下：

驾驶员手驱动方向盘8使转向系统输入功率、圆周运动和扭矩，方向盘8将运动和扭矩传递给方向盘管柱12，方向盘管柱12再将运动和扭矩传递给方向盘传动管柱1，方向盘传动管柱1随之将运动和扭矩传递给花键转换器14，花键转换器14通过方向机将运动和扭矩传递给方向机齿条拉杆22，方向机齿条拉杆22将运动和扭矩传递给右转向节摇臂23，右转向节摇臂23通过销将运动和扭矩传递给转向横拉杆26，转向横拉杆26通过球铰将运动和扭矩同时传递给右转向拉杆24和左转向拉杆28，右转向拉杆24最后通过球铰将运动和扭矩传递给右转向节25及右转向轮，左转向拉杆28最后通过球铰将运动和扭矩传递给左转向节27及左转向轮，左右转向轮同时运动实现汽车转向。

随着汽车载荷从空载开始增加，转向系统传动链从方向盘8到左转向拉杆和右转向拉杆内端点(内端球铰中心)距离地面的高度随着车架同步变化。而左转向拉杆28和右转向拉杆24另一端点(外端球铰中心)距离地面的高度由转向轮决定，左转向拉杆28和右转向拉杆24两端点运动不一致导致左转向拉杆28和右转向拉杆24倾斜，从而驱动左转向拉杆28和右转向拉杆24外端球铰中心绕主销中心线c’转动。左转向拉杆28和右转向拉杆24外端球铰中心运动导致左右转向轮之间夹角改变。左转向轮和右转向轮之间夹角的变化体现转向轮前束的变化，转向轮前束为左转向轮和右转向轮之间的夹角。

左转向拉杆28和右转向拉杆24外端球铰中心绕主销中心线c’转动量不仅决定于车架距地面高度变化，还决定于转向轮内倾角和轮距的变化，以及转向拉杆和转向节的尺寸及位置。

s2：建立满载工况转向拉杆-转向节几何模型；

由于左转向轮和右转向轮为对称结构，且左转向轮、右转向轮分别与左转向节27、右转向节25一起转动。本实施例仅通过右转向拉杆-右转向节几何模型说明汽车满载工况下转向轮前束变化。

在上述的转向系统结构模型下，结合画法几何理论，模拟载荷变化时转向拉杆-转向节传动段运动规律。按照转向系统的投影理论进行投影，绘制投影三视图，反映右转向拉杆24与右转向节25之间几何连接关系，即转向系统的右转向拉杆24至右转向节25传动段。

如图4-6所示，在右转向拉杆-右转向节几何模型中，包括第一端点a、第二端点b和第三端点p。a点(第一端点)表示右转向拉杆24内端球铰中心，b点表示右转向拉杆24外端球铰中心(第二端点)，且为右转向拉杆24与右转向节25的交点，p点(第三端点)表示汽车转向轮中心线与转向轮主销中心线的交点。

右转向轮主销中心线构成第一投影线l1线，第二端点b与第三端点p连接构成第二投影线l2线，bp线(l2线)表示右转向节25，第一端点a和第二端点b连接构成第三投影线l3，ab线(l3线)表示右转向拉杆24。

图4-6中，图中x、y、z为坐标轴，坐标原点为0，箭头所指方向为正方向。a1、a2、a3分别为a点在主视图、俯视图和左视图中的投影点。b1、b2、b3分别为b点在主视图、俯视图和左视图中的投影点。p1、p2、p3分别为p点在主视图、俯视图和左视图中的投影点。α表示主销中心线后倾角，顺时针为正；β表示主销中心线内倾角，顺时针为正。

图4-6为汽车满载直行工况，载荷不变，转向角为0°，a、b、c三个点位置不改变。由于转向轮和转向节为刚性整体，转向轮前束与转向节l2线的相对位置不会改变，此工况对于右转向轮前束为定值，通常为0°。

s3：建立右转向节的转动锥面轨迹三维模型；

在图4-图6所示的满载工况的基础上，模拟右转向节25随载荷变化的运动规律，右转向节25的运动轨迹构成锥面，构建右转向节25的转动锥面轨迹三维模型。

请参阅图7，不考虑右转向拉杆ab线的联接，模拟右转向节pb线的球铰中心b点的运动，以p点为顶点，绕转向轮主销中心线l1线转动形成右转向节pb线的转动锥面，形成以p点为顶点、l1线为锥中心线、高度为h1、底圆半径为r1的圆锥体三维模型。球铰中心b点的回转平面形成上述圆锥体的底圆，随载荷变化，b点的运动轨迹被约束在回转平面的圆周上。

根据满载工况下已知的p点、b点以及l1线方向，采用画法几何投影法求出上述圆锥体的锥面底圆半径r1和圆锥体高度h1。即，r1为b点的运动轨迹半径，h1为p点到b点所在回转平面的距离。

s4：建立右转向拉杆的转动球面三维模型；

在满载工况的基础上，模拟右转向拉杆24随载荷变化的运动规律，右转向拉杆24的运动轨迹构成球体，构建右转向拉杆24的转动球面三维模型。

请参阅图8，不考虑右转向节bp线的联接，模拟右转向拉杆ab线上球铰中心b点的运动，以a点为球心，ab线绕a点转动形成球体，随载荷变化，b点的运动轨迹被约束在球体的球面上。

根据满载工况下已知的a、b点位置，采用画法几何投影法求出上述球体的球面半径sr，即sr为b点的运动轨迹半径。

s5：建立满载工况下，右转向节与右转向拉杆的交点计算三维模型；

利用绘图工具，例如autocad软件，在同一坐标系下，建立右转向节25的转动锥面轨迹三维模型以及转向拉杆24的转动球面三维模型，构建转向节25与转向拉杆24的交点计算三维模型，用于获得转向节25与转向拉杆24交点的位置。

请参阅图9，在autocad软件同一个坐标系下，建立锥面三维模型和球面三维模型，用“交集”命令可以获得b点，称为b点计算三维模型。图9中b为上述圆锥体的锥面底圆与球体的球面交点。用“标注”命令可以获得b点的坐标xb、yb和zb。

s6：确定加载或减载工况下，右转向节与右转向拉杆的交点位置；

在转向系统载荷改变时，根据右转向节与右转向拉杆的交点计算三维模型，获得加载或减载工况下，右转向节与右转向拉杆的交点位置。具体地，根据加载或减载工况下，a点、p点和l1线的不同位置，采用与s5步骤相同的方法，获得加载或减载工况下b点的坐标xb’、yb’和zb’。

在载荷发生改变时，右转向节的转动锥面轨迹三维模型以及右转向拉杆的转动球面三维模型的模型尺寸保持不变，即圆锥体的锥面底圆半径r1、圆锥体高度h1保持不变，球面的半径sr保持不变。载荷改变时，a点、p点和l1线的位置发生改变，在同一坐标系下，右转向节的转动锥面轨迹三维模型以及右转向拉杆的转动球面三维模型发生的位置发生偏转，右转向节与右转向拉杆的交点位置(b点)发生变化。

s7：确定右转向轮前束变化；

在转向系统载荷改变时，右转向节25与右转向拉杆24几何模型发生改变，通过测量转向系统载荷变化前后右转向节25的转动角度获得转向轮前束变化。

请参阅图10，根据右转向节25-右转向拉杆24几何模型，模拟载荷变化前后转向节bp线的不同位置，通过测量载荷变化前右转向节bp线(p2b2线)与载荷变化后的右转向节bp线(p21b21线)之间的夹角δγ，即为载荷变化前后右转向轮前束变化，缩小为正。由于转向轮左右对称，转向轮前束变化为2δγ。

可以理解的是，也可以构建左转向节-左转向拉杆几何模型，通过测量左转向节的转动角度进而获得转向轮前束变化。

下面通过汽车转向轮前束变化计算案例，进一步说明本发明的技术方案。

表1中，坐标系如图4-6所示，xa、ya和za分别为载荷变化前a点在坐标系中的x、y和z坐标，xb、yb和zb分别为载荷变化前b点在坐标系中x、y和z坐标，xp、yp和zp分别为载荷变化前p点在坐标系中x、y和z坐标。xa’、ya’和za’分别为载荷变化后a点在坐标系中x、y和z坐标。xp’、yp’和zp’分别为载荷变化后p点在坐标系中x、y和z坐标。α为主视图上主销中心线与z轴夹角，顺时针为正(主销中心线后倾)；β为左视图上主销中心线与z轴夹角，顺时针为正(主销中心线内倾)；δβ为载荷变化导致β变化；δs为载荷变化导致p点y坐标变化，轮距增加为正。δz为载荷变化a点z坐标变化，减载为正。以上数据由设计给出。

xb’、yb’和zb’分别为载荷变化后b点在坐标系中x、y和z坐标。通过上述描述的建立转向节的锥面三维模型和转动拉杆的球面三维模型后，得到用“交集”命令获得b点的位置。δγ，h1、r1、sr同前面方法所述，由画法几何投影法求得。

通过b点计算三维模型得到满载工况、减载工况和加载工况下，载荷变化前后b点的位置，通过在图10中测量载荷变化前后pb线的的夹角δγ，获得前束变化。在图10中，a2、b2、p2为满载工况下a点、b点、p点在俯视图上投影。a2、b21、p21为减载(加载)工况下a点、b点、p点在俯视图上投影。在图10上测量p21b21与p2b2夹角δγ，即为减载(加载)工况右转向轮前束变化，总前束变化为2δγ(°)。通过测量可得，满载工况下，载荷变化前后，前束变化为2δγ(°)＝2×(0°)＝0°。加载工况下，载荷变化前后，前束变化为2δγ(°)＝2×(2.88°)＝5.76°。减载工况下，载荷变化前后，前束变化为2δγ(°)＝2×(-3.86°)＝-7.72°。

表1汽车转向轮前束变化计算方案与结果

以上所述仅为本发明的优选实施方式而已，并不用于限制本发明，对于本领域的技术人员来说，本发明可以有各种更改和变化。凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。