一种基于合作博弈的混合执行机构动量优化管理方法与流程

本发明属于卫星姿态控制技术领域，尤其涉及一种基于合作博弈的混合执行机构动量优化管理方法。

背景技术

随着航天任务复杂性的不断提高，卫星敏捷机动以及姿态动态跟踪任务等成为航天器姿态控制的研究热点。如法国的pleiades高分辨率成像卫星，其姿态机动角速度要求达到3deg/s；又如美国的预警卫星xss-10，其在执行遥测和跟踪任务时，需在进行姿态大角度机动的同时，对目标进行高精度姿态动态跟踪。显然，敏捷机动和姿态动态跟踪对执行机构具有较高的要求，一方面需要执行机构输出较大的姿态控制力矩，另一方面要求执行机构输出的力矩具有较高的精度。

传统的姿态控制执行机构包括推力器、飞轮(reactionwheel,rw)、控制力矩陀螺(controlmomentgyro,cmg)、磁力矩器等。但单一种类执行机构存在各自的局限性，例如推力器需要消耗推进剂，从而影响卫星的在轨寿命；rw的输出力矩相对较小，无法满足敏捷机动控制要求；cmg的输出力矩虽然较大但是存在固有的奇异问题，无法满足高精度控制要求；磁力矩器输出力矩太小，只能用于rw卸载及cubesat等质量较小卫星的姿态控制等。因此，敏捷机动卫星和姿态动态跟踪卫星通常采用混合执行机构，而基于cmg和rw的混合执行机构cmgrw具有大力矩输出，控制精度高的特点，满足上述任务要求。

由于cmg具有几何奇异问题，rw具有饱和问题，如何使cmg和rw协同工作成为混合执行机构cmgrw控制律设计的主要问题，即如何同时解决cmg奇异问题和rw饱和问题。中国科学院长春光学精密机械与物理研究所的范国伟等设计了一种面向成像敏捷卫星的混合执行机构控制方法，针对cmg和rw混合执行机构，由legendre伪谱法前馈控制和实现最优轨迹的反馈控制组成，前馈控制可实现cmg系统框架角速度的最优规划；反馈控制以飞轮输出力矩等作为约束，补偿初始状态和转动惯量偏差导致的控制误差，但该方法采用最优轨迹，难以满足高动态实时性的要求。上海航天控制工程研究所的耿淼等针对卫星快速机动设计了一种混合执行机构控制方法，但该控制方法仅适用单轴姿态快速机动任务。北京航空航天大学的王焕杰等基于高斯伪普法设计了基于cmg和rw的混合执行机构控制律，解决了cmg奇异问题，但可能会造成rw和cmg频繁切换。哈尔滨工业大学的耿云海等设计了一种基于cmg与rw混合执行机构的力矩分配算法，能够解决cmg奇异问题和死区问题以及rw的饱和及过零问题，但未实现rw和cmg优化管理，系统的能量消耗较高。

技术实现要素：

发明目的：本发明目的是提供一种基于合作博弈的混合执行机构动量优化管理方法，能够使cmg和rw协同工作，解决cmg的奇异问题和rw的饱和问题。

技术方案：本发明包括以下步骤：

(1)设计cmgrw混合执行机构控制的策略目标和约束条件其中为cmg的框架角速度，为rw的旋转角加速度；

(2)根据策略目标和约束条件设计合作博弈论度量函数其中λ＝[λ1,λ2,λ3]为策略组合；

(3)定义策略组合λ＝[λ1,λ2,λ3]和cmg框架角速度以及rw旋转角速度之间的关系得到

(4)进行模糊聚类，得到cmgrw混合执行机构的策略空间η1、η2和η3，策略空间满足合作博弈论度量函数，且策略组合λ＝[λ1,λ2,λ3]满足λ1∈η1、λ2∈η2和λ3∈η3；

(5)选择cmgrw混合执行机构初始策略组合λ0＝[λ10,λ20,λ30]，固定初始策略组合λ0＝[λ10,λ20,λ30]；

(6)设计策略组合的变化值δλ＝[δλ1,δλ2,δλ3]，分别对λ1,λ2,λ3进行单目标优化；

(7)假如变化值满足h(dλ)≤0，则进入步骤(8)；否则，进入步骤(5)；

(8)使λ＝λ+dλ，得到cmgrw混合执行机构新的策略组合假如策略组合收敛，则进入步骤(9)，否则，使λ0＝λ^#，并进入步骤(6)；

(9)得到最佳策略组合λ^*＝λ^#，博弈结束。

所述步骤(1)中的策略目标和约束条件由cmg奇异条件和rw饱和条件决定。

所述的cmgrw混合执行机构包括n个cmg组成的cmg系统以及m个rw组成的rw系统。

所述的cmgrw混合执行机构采用混合执行机构合作博弈论控制律进行控制。

所述的混合执行机构合作博弈论控制律为：

其中，u为控制力矩，为cmg框架角速度和rw角加速度的集合，a为混合执行机构的系统矩阵，并与混合执行机构的构型有关。

有益效果：本发明首次采用合作博弈论设计基于cmg和rw混合执行机构控制律，避免了rw饱和以及cmg的奇异问题，并且能高精度地输出大力矩，提高了卫星姿态机动敏捷能力，并通过管理和优化角动量，达到能量优化的目的，同时降低混合执行机构系统的能量消耗。

附图说明

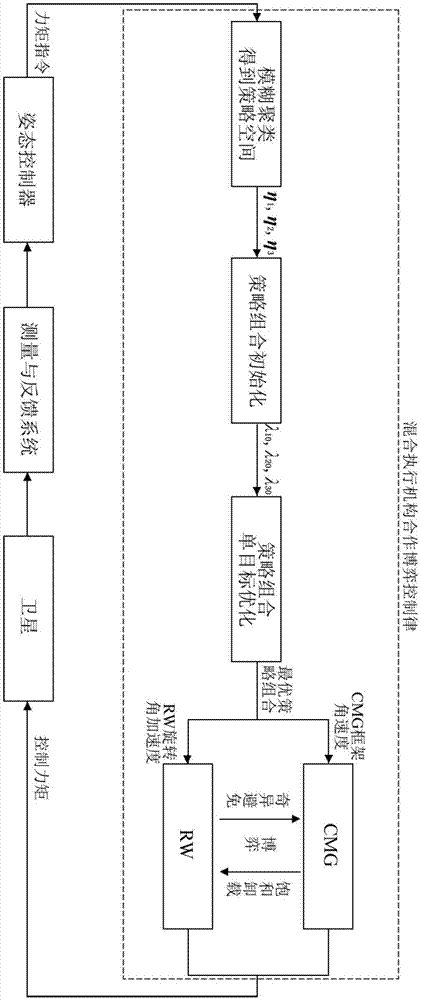
图1为本发明的cmgrw混合执行机构控制框图；

图2为本发明的混合执行机构控制律设计流程示意图。

具体实施方式

下面结合附图对本发明作进一步说明。

如图2所示，本发明包括以下步骤：

(1)设计cmgrw混合执行机构控制的策略目标和约束条件其中为cmg的框架角速度，为rw的旋转角加速度；

(2)根据策略目标和约束条件设计合作博弈论度量函数其中λ＝[λ1,λ2,λ3]为策略组合；

(3)定义策略组合λ＝[λ1,λ2,λ3]和cmg框架角速度以及rw旋转角速度之间的关系得到

(4)进行模糊聚类，得到cmgrw混合执行机构的策略空间η1、η2和η3，策略空间满足合作博弈论度量函数，且策略组合λ＝[λ1,λ2,λ3]满足λ1∈η1、λ2∈η2和λ3∈η3；

(5)选择cmgrw混合执行机构初始策略组合λ0＝[λ10,λ20,λ30]，固定初始策略组合λ0＝[λ10,λ20,λ30]；

(6)设计策略组合的变化值δλ＝[δλ1,δλ2,δλ3]，分别对λ1,λ2,λ3进行单目标优化；

(7)假如变化值满足h(dλ)≤0，则进入步骤(8)；否则，进入步骤(5)；

(8)使λ＝λ+dλ，得到cmgrw混合执行机构新的策略组合假如策略组合收敛，则进入步骤(9)，否则，使λ0＝λ^#，并进入步骤(6)；

(9)得到最佳策略组合λ^*＝λ^#，博弈结束。

步骤(1)中的策略目标和约束条件由cmg奇异条件和rw饱和条件决定。如图1所示，cmgrw混合执行机构在混合执行机构合作博弈论控制律的控制下进行博弈，cmgrw混合执行机构包括n个cmg组成的cmg系统以及m个rw组成的rw系统。混合执行机构合作博弈论控制律为二次规划问题，并且对执行机构的角动量进行优化。混合执行机构合作博弈论控制律为：

其中，u为控制力矩，为cmg框架角速度和rw角加速度的集合，a为混合执行机构的系统矩阵，并与混合执行机构的构型有关。