一种卫星化学推进变轨方法及系统与流程

本发明涉及卫星轨道控制领域，具体涉及一种卫星化学推进变轨方法及系统。

背景技术：

导航卫星(例如北斗卫星)通常位于地球静止轨道geo或者倾斜地球同步轨道igso。从地面发射之后，运载器将卫星转移至地球同步转移轨道gto轨道，之后卫星利用自身的推进系统完成geo/igso的入轨飞行。

航天时代以来，化学推进一直是航天器轨道机动的主力。虽然近些年电推进逐渐崛起，但是在可见的未来里，化学推进依旧有推力大，机动时间短等难以替代的优势。在轨道的转移过程中，化学推进能使航天器较快入轨。

由于化学推进的上述优势，在解决变轨问题时，常使用脉冲假设简化问题。论文“ananalyticalstudyoftheimpulsiveapproximation.aiaajournal,vol.4,no.8(1966),pp.1417-1423.”中给出了脉冲假设的理论依据，说明在化学推进弧段较短时与理想脉冲假设误差较小。因此对于无约束的gto至geo的轨道转移，理想情况下可通过一次远地点机动完成。

而在实际工程任务里，转移过程常有测控、单次最大点火时长、化学推进弧段误差等诸多约束。目前，我国的测控站在全球范围内分布尚较为稀疏，因此考虑单观测站约束下gto至geo的变轨具有一定的战略意义。

论文“嫦娥一号卫星的地月转移变轨控制[j].空间控制技术与应用,2008(01):44-50.”分别选取了轨道周期为16h、24h以及48h的三个与地球自转周期匹配的停泊轨道，使用了数次远地点变轨在满足观测、点火时长约束的条件下完成了嫦娥一号奔月的变轨要求，但该方案是仅针对于嫦娥一号奔月任务做的变轨设计，并不适合从gto至geo的轨道转移。且其只给出了方案设计结果，并未给出详细的方案思路及设计过程，不具有通用性。

除此之外，geo的重要性更是毋庸置疑。由于天然的动力学特性，geo卫星能够对固定区域进行全时、长期覆盖，具有独特的优势。目前的在轨卫星中有近三分之一位于geo。

论文“operationallyoptimalmaneuverstrategyforspacecraftinjectedintosub-geosynchronoustransferorbit.40thcosparscientificassembly.vol.40.2014.”设计了印度的gsat-12同步轨道通信卫星的变轨过程。卫星的初始轨道为近地点高度284km、远地点高度21000km、倾角为18°的亚gto轨道。提出并分析了三种变轨策略，均由数次近地点与远地点变轨组成。该方案依据经验与具体任务需求制定的变轨策略，因此其设计方法仅适用于特定任务，对于其它类似任务只具有一定程度的参考意义，且其在设计过程中考虑了双观测站，不适用于单观测站的情况。

技术实现要素：

针对上述技术问题，本发明提供一种卫星化学推进变轨方法及系统。

本发明解决上述技术问题的技术方案如下：一种卫星化学推进变轨方法，针对卫星从地球同步转移轨道gto向地球静止轨道geo采用化学推进变轨的场景，包括：

步骤1、根据发动机推力及单次最大推进时长约束，依次选择一个或者多个变轨过程中的停泊轨道；

步骤2、根据所述gto、geo和各停泊轨道的轨道参数，分别计算每次变轨所需的速度增量；

步骤3、根据所述速度增量计算每次变轨的机动时间；

步骤4、根据所述机动时间计算每次变轨的机动开始时刻；

步骤5、根据所述速度增量确定每次变轨的推力方向；

步骤6、按照所述机动时间、机动开始时刻和推力方向实施变轨。

为实现上述发明目的，本发明还提供一种卫星化学推进变轨方法，针对卫星从地球同步转移轨道gto向倾斜地球同步轨道igso采用化学推进变轨的场景，其特征在于，假设gto的近地点与远地点位于igso内，以igso轨道作为赤道面，重新定义轨道倾角：

其中，npark与nigso分别是停泊轨道与igso轨道平面的法向量，表示如下：

其中i(·)，ω(·)分别为相应轨道的升交点赤经与轨道倾角；

则所述方法包括：

步骤1、根据发动机推力及单次最大推进时长约束，依次选择一个或者多个变轨过程中的停泊轨道；

步骤2、根据所述gto、igso和各停泊轨道的轨道参数，分别计算每次变轨所需的速度增量；

步骤3、根据所述速度增量确定每次变轨的推力方向；

步骤4、根据所述速度增量计算每次变轨的机动时间；

步骤5、根据所述机动时间计算每次变轨的机动开始时刻；

步骤6、按照所述机动时间、机动开始时刻和推力方向实施变轨。

本发明还提供一种卫星化学推进变轨系统，针对卫星从地球同步转移轨道gto向地球静止轨道geo采用化学推进变轨的场景，该系统包括：

停泊轨道选取模块，用于根据发动机推力及单次最大推进时长约束，依次选择一个或者多个变轨过程中的停泊轨道；

速度增量计算模块，用于根据所述gto、geo和各停泊轨道的轨道参数，分别计算每次变轨所需的速度增量；

机动时间计算模块，用于根据所述速度增量计算每次变轨的机动时间；

机动开始时刻计算模块，用于根据所述机动时间计算每次变轨的机动开始时刻；

推力方向确定模块，用于根据所述速度增量确定每次变轨的推力方向；

变轨实施模块，用于按照所述机动时间、机动开始时刻和推力方向实施变轨。

本发明的有益效果是：通过选择合适的停泊轨道与相应停泊轨道下脉冲初值的分次优化，从而得到了单观测站约束情况下由gto至geo的轨道转移化学推进解，具有较强的普适性，并且能够较为容易地扩展到至igso轨道的转移。

附图说明

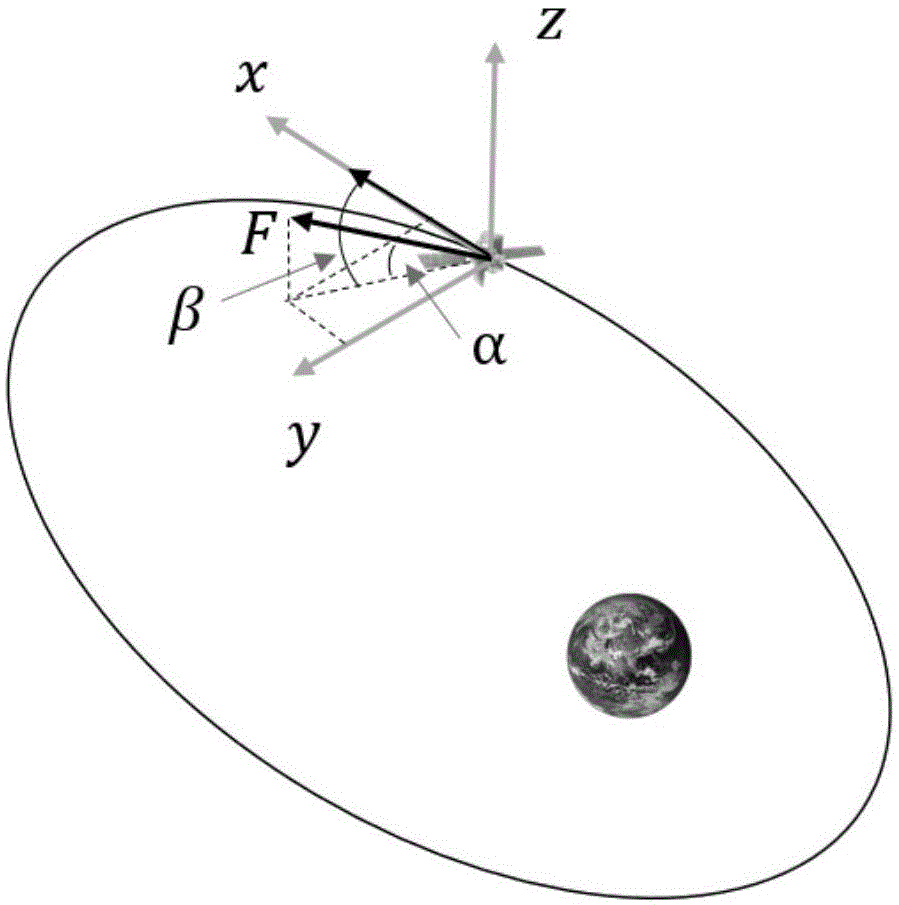
图1为vnc坐标系示意图

图2为本发明实施例提供的一种卫星化学推进变轨方法的流程图；

图3为脉冲变轨示意图；

图4为变轨过程的轨道仿真图(文昌)；

图5为变轨中的星下点经度(文昌)；

图6为变轨过程的轨道仿真图(西昌)；

图7为变轨中的星下点经度(西昌)；

图8入轨半长轴与geo的差；

图9入轨偏心率与geo的差；

图10入轨倾角与geo的差。

具体实施方式

以下结合附图对本发明的原理和特征进行描述，所举实例只用于解释本发明，并非用于限定本发明的范围。

考虑单站观测约束下使用化学推进将卫星从gto(地球同步转移轨道)变轨至geo(地球静止轨道)的轨道转移问题。通常gto为大偏心率椭圆轨道，其远地点半径42164公里，且位于地球赤道平面上，标准周期约为10.5小时。而geo为圆轨道，轨道半径42164公里，位于地球赤道面上，轨道周期24小时。

相比于传统gto至geo的变轨问题，本发明考虑了两个现实约束：

(1)观测约束：每次变轨段，卫星的星下点经度均在观测站附近；

(2)推进约束：发动机每次点火都有最大开机时长约束，一般为小时量级。

事实上gto到geo的转移实为完成两类轨道操作，即提升轨道高度和降低轨道倾角，因此发动机推力方向需具有速度方向和轨道面法向的分量。前面提及观测约束要求每次点火均位于一定的地理经度范围内，而推进约束则是限制了每次的机动能力。两者的协同约束使得整个机动需要分为多次进行。每次机动由发动机推力方向、以及点火起始和结束时刻决定。因此，本发明旨在确定点火次数、并给出每次点火的发动机推力方向、点火起始时刻以及点火结束时刻。

用于变轨的化学推进发动机一般可提供数百牛的推力，化学推进与脉冲相互转化存在一定的误差，这些误差可能会改变gto的轨道朝向、方位等几何特性。因此，机动前后轨道自身的几何约束也是设计时需要考虑的关键问题。

由于存在工程约束，变轨时间为数天，摄动会对卫星轨道造成不可忽略的影响，因此本专利的轨道转移问题需能够适用于高保真动力学环境下。为此，本专利采用层次化策略，首先在二体模型下设计转移策略，之后以其作为初值在高保真动力学环境中优化。这里高保真动力学环境包括地球的21x21阶引力场、太阳光压模型以及日月第三体引力。

因此，gto/geo化学推进的核心在于高保真环境下定义和分配每次机动的目标，进而求解出推力方向和点火时刻。

由于脉冲机动和化学推进的关联，解决本问题的方案为：

(1)根据gto倾角、发动机推力及单次推进时长约束，选取卫星从地球同步转移轨道gto向地球静止轨道geo化学推进变轨的停泊轨道；

(2)在二体动力学环境中和脉冲假设下，根据所述gto、geo和停泊轨道的轨道参数，分别计算每次变轨所需的速度增量，进而计算每次变轨的机动时间、机动开始时刻、以及推力方向，并根据计算结果选择相应的优化方案；

(3)将所述的每次变轨的机动时间、机动开始时刻、以及速度增量在二体动力学环境中进行优化，以得到二体动力学环境下的化学推进解。并进而将二体动力学环境下的化学推进解在高保真动力学环境中进行优化，以得到适用于实际动力学环境的化学推进解。对于每次变轨，上述两步优化使用相同的优化策略。

另外，本发明所用的坐标系为vnc(velocity-normal-co-normal)坐标系。具体定义如下：如图1所示，坐标原点o位于卫星质心，x轴为速度方向，y轴为轨道面法向，z轴与前两者组成右手直角坐标系。本坐标系用于描述推力方向。在vnc坐标系中，推力方向由两个方向角α和β表示，其中α为推力方向与xy平面的夹角，而β表示推力方向在xy平面投影与x轴的夹角。

实施例一

图2为本发明实施例提供的一种卫星化学推进变轨方法的流程图，针对卫星从地球同步转移轨道gto向地球静止轨道geo采用化学推进变轨的场景，该方法包括：

s1、根据发动机推力及单次最大推进时长约束，依次选择一个或者多个变轨过程中的停泊轨道；

由于在远地点改变倾角所需的脉冲最小，并且gto在远地点与geo相交且内切，因此卫星施加一个远地点脉冲即可有效完成变轨。在本问题中，由于化学推进的推进约束会限制脉冲大小，理想情况下的一次远地点脉冲需分为多次远地点脉冲，因此要选取数个中间停泊轨道。整个轨道机动过程如下：

其中单次机动如图3所示。

假设gto入轨较为精确，发射窗口选则使得卫星在某次到达gto远地点时，星下点经度位于观测站附近。卫星在该次到达远地点时做第一次变轨，转移过程中的中间停泊轨道的选择方式如下：

s1.1、按照下列匹配关系确定所述各个停泊轨道的轨道周期：

其中，tpark为停泊轨道的轨道周期，tearth为地球自转周期，n与m为互质整数，且n<m。这意味着对于停泊轨道来说，每经过m个停泊轨道周期，也即n个地球自转周期，卫星会重新回到相同的星下点经度。如此即可在每次变轨处满足观测约束。由于每次远地点变轨提升近地点高度，停泊轨道的半长轴会越来越大，直至与geo轨道高度相同。因此n/m的上界是1；下界则由gto的轨道周期决定，对于典型的gto，其近地点高度为200km，远地点位于geo，周期约为geo的0.44倍，即为n/m的下界。考虑到n与m越小，所需等待时间越短，因此一般n/m取为1/2、2/3、3/4等。

停泊轨道的选取还会受到脉冲大小的约束，应在脉冲约束范围内选取合适的停泊轨道。

s1.2、根据所述轨道周期计算本次变轨的停泊轨道的远地点速度；

s1.3、判断所述远地点速度是否满足所述发动机推力及单次最大推进时长约束，若是则继续选择下一次变轨的停泊轨道的轨道周期，直至变轨完成，否则重新确定本次变轨的停泊轨道的轨道周期。

具体的，步骤s1.2和s1.3的具体计算过程如下：

计算脉冲解的算法：

输入参数为：gto轨道参数(agto,igto)，gto卫星质量m，最大机动时间tmax。输出参数为：总的机动次数；每次机动的起始时刻、点火时间、推力方向；每次机动后的轨道信息、卫星质量。

初始化：，变轨前轨道记作x^-＝(agto,igto)，变轨前卫星质量记作m^-＝m；变轨后轨道初始化为x⁺＝x^-；

若变轨后目标不是geo，即x⁺≠(ageo,0)，重复进行如下步骤1、2、3、4、5直到变轨后轨道为geo：

1.计算本次最大脉冲机动能力：

其中g为海平面重力加速度。

2.设计变轨后目标轨道轨道，并计算速度脉冲：

x^-,δvmax→x⁺,δv

3.计算燃料消耗和变轨后卫星质量：

m⁺＝m^--δm

机动次数加一。

4.给出每次机动的起始时刻t，点火时长δt，其中点火时长δt的计算公式为：

保存x⁺,δv,δm,t,δt,β。

5.更新：变轨前轨道＝变轨后轨道，变轨前质量＝变轨后质量，记作

x^-＝x⁺,m^-＝m⁺,

对于前述算法中第2步，详细展开如下：

该步骤的目标是，根据给定变轨前轨道参数x^-＝(a^-,i^-)和脉冲机动能力δvmax，给出变轨的目标停泊轨道x⁺＝(a⁺,i⁺)和速度脉冲δv。

具体的计算过程如下：

a.计算变轨前远地点速度

其中μ为地球引力常数。

b.选定目标轨道半长轴

半长轴选定原则为周期简单通约，即且a⁺＞a^-。这里pgeo为geo轨道周期，即24小时。

令初始化δv＝+∞,k＝1。

若δv＞0时，重复如下步骤直到δv满足δv＜0：

计算下列参数：

p⁺＝pgeosk,

δv＝v⁺-v^--δvmax

k＝k+1

这里p⁺,a⁺,v⁺分别为待选轨道的周期、半长轴、远地点速度，δv是脉冲机动的欠缺量。输出变轨目标停泊轨道的半长轴a⁺和速度v⁺。

c.选定轨道倾角

计算变轨目标停泊轨道倾角

输出停泊轨道倾角为i⁺，至此，得到停泊轨道参数x⁺＝(a⁺,i⁺)。

另外，针对卫星从地球同步转移轨道gto向倾斜地球同步轨道igso采用化学推进变轨的场景，将igso看做一个新的参考面，对设计过程做如下转换：

(1)假设gto的近地点与远地点位于igso内；

(2)以igso轨道作为赤道面，按照下式重新定义轨道倾角：

其中，npark与nigso分别是停泊轨道与igso轨道平面的法向量，表示如下：

其中i(·)，ω(·)分别为相应轨道的升交点赤经与轨道倾角。

后续计算即可按照与geo变轨相同的思路进行。

s2、根据所述gto、geo和各停泊轨道的轨道参数，分别计算每次变轨所需的速度增量；

s3、根据所述速度增量确定每次变轨的推力方向；

具体的，在确定停泊轨道后，即可根据gto、geo和停泊轨道的轨道参数，分别计算gto、各个停泊轨道和geo中的相邻轨道的远地点速度之差，从而得到每次变轨所需的速度增量。

具体的计算过程如下：

相应的速度脉冲投影在轨道坐标系vnc中

其大小和方向为

δv＝||δv||

这里β是推力与轨道面的夹角。

s4、根据所述速度增量计算每次变轨的机动时间；

如上设计出合适的停泊轨道，可同时满足观测和脉冲约束，得到脉冲解。对于每次脉冲变轨，可通过下式计算每次变轨的机动时间：

其中，i＝1...n，n为变轨次数，δti为第i次变轨的机动时间，mi为卫星在第i次变轨前的整星质量，δvi为第i次变轨所需的速度增量，||·||为取模，f为发动机推力，g为海平面重力加速度，isp为比冲。

s5、根据所述机动时间计算每次变轨的机动开始时刻；

具体的，由于gto的轨道倾角的存在，每次变轨需使近地点辐角保持在180°附近，以保持远地点在赤道面附近。根据高斯摄动方程(r为经典轨道根数矢量，gu(r)与gp为高斯摄动方程的系数矩阵，f为发动机推力，m(t)为航天器质量)：

需保持机动过程关于远地点近似对称，方能使近地点辐角在180°附近，同时使化学推进对轨道根数的影响接近脉冲解。因此将机动看做关于远地点时间对称，则可以推算得出变轨的机动开始时刻，也即用远地点脉冲变轨时刻减去一半的变轨机动时间，即可得到机动开始时刻。

s6、按照所述机动时间、机动开始时刻和推力方向实施变轨。

可选地，在该实施例中，在步骤s5和s6之间，该方法还包括：

s7、根据每次变轨的停泊轨道的轨道参数，选择相应的优化方案；

s8、依据所述优化方案，采用二体动力学模型进行卫星轨道递推，将化学推进初值优化为所述二体动力学模型下的化学推进解，其中，所述化学推进初值包括所述推力方向、机动时间和机动开始时刻；

优化问题的描述见下表：

表1优化策略表

其中ε(·)代表各项约束的允许误差，|p-pt|＜εt表示机动后轨道周期应该与设计的停泊轨道一致，|ω-π|＜εω表示机动后轨道近地点幅角应当在180度附近，e＜εe表示机动后轨道应该近圆，|t-t0|＜εt,|δt-δt0|＜εδt,|β-β0|＜εβ表示每次机动的起始时刻、时长、推力方向应当与脉冲初值接近。

s9、依据所述优化方案，对于每次机动，采用高保真动力学模型作为卫星轨道递推，卫星轨道根数采用平均根数，将所述二体动力学模型下的化学推进解优化为所述高保真动力学模型下的化学推进解；

优化问题的描述同上表1。平均根数的具体算法可参见brouwer-lyddane的文献(smalleccentricitiesorinclinationsinthebrouwertheoryoftheartificialsatellite,"r.h.lyddane,theastronomicaljournal,oct.1963,pp.555-558.)

在得到高保真动力学模型下的化学推进解后，即可按照高保真动力学模型下的化学推进解实施变轨。

具体的，通过步骤s1-s5，可以得出约束下脉冲变轨的化学推进初值，也即每次化学推进变轨的起始时刻、持续时间、以及推力方向的初值。考虑到摄动会对卫星轨道造成一定影响，需要将该初值代入二体动力学方程进行优化，再以二体动力学下的优化结果作为初值代入高保真动力学模型优化，如步骤s7-s9，即可得到最终的化学推进变轨方案，也即最终的变轨起始时刻、变轨持续时间以及推力方向。

实施例二

本发明实施例提供一种卫星化学推进变轨系统，该系统中各个模块的功能原理已在前面进行了详细阐述，以下不再赘述。

针对卫星从地球同步转移轨道gto向地球静止轨道geo采用化学推进变轨的场景，该系统包括：

停泊轨道选取模块，用于根据发动机推力及单次最大推进时长约束，依次选择一个或者变轨过程中的停泊轨道；

速度增量计算模块，用于根据所述gto、geo和各停泊轨道的轨道参数，分别计算每次变轨所需的速度增量；

机动时间计算模块，用于根据所述速度增量计算每次变轨的机动时间；

机动开始时刻计算模块，用于根据所述机动时间计算每次变轨的机动开始时刻；

推力方向确定模块，用于根据所述速度增量确定每次变轨的推力方向；

变轨实施模块，用于按照所述机动时间、机动开始时刻和推力方向实施变轨。

实施例三

本部分根据实施例一中的策略对于一个具体问题的两种情况给出了详细的设计过程与设计结果，以给出直观的应用说明，并证明本专利的有效性和普适性。具体问题描述如下：

卫星的初始整星质量m0为4000kg，其中燃料质量为3000kg，发动机推力大小f恒定，为490n，比冲isp为315s，每次点火最大开机时长tmax为1.5h。在第一个算例中，将文昌(19.7°n，110.8°e)作为观测站和发射基地；在第二个算例中，则以西昌(28.2°n，102.0°e)作为观测站和发射基地。观测约束要求每次变轨段，卫星的星下点经度与观测站经度差小于30°。在两个算例的方案设计中，文昌与西昌采用了0不同的优化策略。

一、文昌变轨方案设计

1脉冲变轨

(1)基本分析

初始时刻，gto的近地点高度为200km，远地点高度为35786.2km，倾角为19.7°，因此可通过下式估算出总速度增量：

其中vgto为卫星位于gto远地点时的速度大小，约为1.597km/s，vgeo为卫星位于geo的速度大小，约为3.075km/s。因此所需的总速度增量约为1.661km/s。

计算出第一次变轨发动机能提供的最大速度增量为：

在之后的变轨中，由于总质量的减小，每次变轨发动机所能提供的最大速度增量均会大于0.744km/s。

可推测经过两至三次变轨即可将卫星变轨至geo。由于gto的周期约为10.52h，而地球自转周期约为23.93h，初步选取两个停泊轨道，其n/m分别为1/2和2/3，分别用下标1和2表示。

(2)脉冲分配

选择第一个停泊轨道的周期比为2/3，其半长轴a1为32177km，远地点速度v1为2.553km/s。改变半长轴所需的速度增量为

δv1＝v1-vgto＝0.956km/s＞δv1_max＝0.744km/s

故2/3的停泊轨道超出了当前机动能力。因此，进一步选择停泊轨道的周期比为1/2，其半长轴a1为26561.7km，远地点速度v1为1.975km/s。对于第一次变轨，改变半长轴所需的速度增量为

δv1＝v1-vgto＝0.378km/s＜δv1_max＝0.744km/s

因此1/2的停泊轨道处于机动能力范围内，并且可在升轨的同时减小倾角。

进而计算

cosigto＝0.942＞ρ

表明第一次变轨可将倾角变为零，后续变轨只需考虑抬高轨道高度即可。

计算第一次变轨的总脉冲、推力方向和机动时间为

α＝0,β＝-1.015

δt1＝5213s

以及变轨后卫星质量为m1＝3172kg

对于第二次变轨，首先计算最大允许脉冲为

由于

vgeo-v1＝1.099km/s＞δv2_max＝0.972km/s

故仍然需要第二个中间停泊轨道，选择其周期为2/3，其半长轴a2为32177km，远地点速度v2为2.553km/s。进一步计算得到，

δv2＝v2-v1＝0.578km/s＜δv2_max＝0.972km/s

故2/3周期的停泊轨道符合要求。

计算第二次变轨的总脉冲和机动时间为

δv2＝δv2＝0.972km/s

α＝0,β＝0

δt2＝3415s

以及变轨后卫星质量为m2＝2630kg。

对于第三次变轨，首先计算最大允许脉冲为

由于

vgeo-v2＝0.521km/s＜δv3_max＝1.217km/s

故本次机动可以实现geo入轨，计算第三次变轨的总脉冲和机动时间为

δv3＝0.521km/s

α＝0,β＝0

δt3＝2575s

以及变轨后卫星质量为m3＝2222kg。

至此，我们得出了在问题约束下的轨道转移脉冲解。

2化学推进变轨

(1)初值

将机动时间看做关于远地点对称，则可以推算得出第一次变轨的机动开始时刻。第二次以及第三次变轨的初始变轨过程与变轨时间可以以相同方法确定。

至此，我们得到了化学推进变轨的全部初始解。

(2)优化

在优化时，为获取到更好的初值，先将以上得到的初值放到二体动力学环境中优化，然后将优化得到的结果作为初值，在高保真动力学环境中进行优化。这两步优化均使用分次优化策略——即对于每次变轨单独优化，优化算法采用matlab的“fmincon”函数中的“interior-point”，下表给出了三次变轨优化过程的指标以及约束：

表2变轨优化指标及约束

3设计结果验证

该算例中，历元初始时刻为2019年4月20日21:30:00.000utc，在历元初始时刻卫星的轨道根数为[24371.2,0.730086,0.3421,0,3.1416,0](依次为半长轴a(km)、偏心率e、倾角i(rad)、升交点赤经ω(rad)、近地点辐角ω(rad)、真近点角m(rad))。

脉冲变轨的设计结果如下：

表3脉冲变轨设计结果

化学推进变轨的设计结果如下：

(1)二体动力学下优化初值

表4变轨优化初值(二体动力学)

(2)二体动力学下变轨优化结果

表5变轨优化结果(二体动力学)

(3)高保真动力学环境下变轨优化结果

表6变轨优化结果(高保真动力学环境)

轨道的仿真结果如图4所示：其中黑色轨道为标准的geo，从内至外的橘色轨道分别为gto、停泊轨道1、停泊轨道2、最终的入轨轨道。第三次变轨后的轨道的半长轴与标准geo的偏差约为184km，轨道周期与地球自转周期差约565秒，偏心率为1.354×10^-7，倾角为0.0071°，三者均达到geo卫星的普遍精度，轨位以及半长轴可在调相过程中得以校正。

图5则是整个变轨过程中的星下点经度，可以看出，三次变轨均符合观测要求，且留有很大裕量。

二、西昌变轨方案设计

1脉冲与化学推进变轨

类似于文昌变轨方案，在西昌变轨方案设计中亦选取n/m分别为1/2和2/3的两条停泊轨道。但所不同的是在三次变轨中，第一次变轨不足以消除倾角，第二次变轨才能将倾角减小至0，因此前两次变轨的脉冲设计与优化过程与西昌变轨方案有所不同。各次变轨优化指标及约束如下：

表7变轨优化指标及约束

2设计结果验证

该算例中，历元初始时刻为2019年4月20日22:10:00.000utc，在历元初始时刻卫星的轨道根数为[24371.2,0.730086,0.4922,0,3.1416,0]。

脉冲变轨的设计结果如下：

表8脉冲变轨设计结果

化学推进变轨的设计结果如下：

(1)二体动力学下优化初值

表9变轨优化初值(二体动力学)

(2)二体动力学下变轨优化结果

表10变轨优化结果(二体动力学)

(3)高保真动力学环境下变轨优化结果

表11变轨优化结果(高保真动力学环境)

轨道的仿真结果如图6所示。第三次变轨后的轨道的半长轴与标准geo的偏差为224km左右，与地球自转的周期差为688秒，偏心率为9.4×10^-8，倾角为0.0037°，三者亦均达到geo卫星的普遍精度。

整个变轨过程中的星下点经度如图7所示，可以看出，三次变轨均符合观测要求，且留有很大裕量。

3总体分析

由西昌与文昌算例的优化结果可以看出，优化结果与脉冲推算结果较为相近，其中机动时间的变化在几十秒量级，这说明脉冲变轨与化学推进变轨在速度增量上的误差较小，因此该方法所需的速度增量接近理想一次脉冲的速度。

另外，在西昌与文昌算例的基础上，又优化了多个倾角不同的算例(0.5°-40°，间隔0.5°)，三者最终的入轨精度如图8-10所示。可以看出，所有算例的半长轴差在450km以下，偏心率与倾角则分别小于1.2×10^-7与0.025°，三者均满足geo的入轨精度，这说明了本方案的有效性与普适性。

实施例四

本发明的关键点有两个：周期匹配停泊轨道的选取，以及在每次变轨优化过程中优化指标的选取。

周期匹配的停泊轨道使得每次在远地点变轨都能够有与第一次变轨处几乎相同的地面站可观测性。因此只需要保证第一次变轨可以观测到，则后续的变轨过程均在地面站可观测范围内。

由于每次停泊轨道不同，因此针对每次变轨优化过程中，需选取不同的优化指标，以使卫星完成消除倾角或轨道圆化。同时还需对变轨后停泊轨道与设计停泊轨道间的周期进行约束，以尽量减少每次的地面可见时间偏移，使得最终的可观测性与预期的差别在容许范围内。

本发明解决了单观测站约束情况下由gto至geo的轨道转移问题，并且能够较为容易地扩展到至igso轨道的转移。本方案所使用的思路较为简洁，因此方案明晰，计算量较小，便于理解，且经验证行之有效，普适性强，只需保证第一次变轨时可观测且留有稍许裕量，则所有变轨皆可观测。另外，仿真结果显示，本方案所需速度增量接近理想脉冲变轨的速度增量，所需燃耗较小。

以上所述仅为本发明的较佳实施例，并不用以限制本发明，凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。