一种平动点轨道交会无需初始误差符号的预设性能控制方法与流程

本发明属于深空航天器自主交会技术领域，涉及一种速度信息缺失、控制器初始误差符号未知的基于三阶积分链微分器的平动点轨道交会自主控制方法。

背景技术：

近年来，随着平动点动力学性质研究的不断深入，平动点轨道展现出巨大的应用前景。世界各国已经发射和正在构想多个平动点观测平台和载人空间站，这些大型航天器的费用高昂，如果发生故障就直接废弃则代价过大，因此，研究平动点轨道航天器的交会对接对于平动点轨道附近航天器的拦截、修复、营救是至关重要的，并且平动点空间飞行器维护系统的成功，将带动深空航天器的重复使用，降低航天成本。

现有的方法大都针对全状态已知的情形对平动点轨道交会问题进行了研究(参考文献1：lianyj,tanggj.librationpointorbitrendezvoususingpwpfmodulatedterminalslidingmodecontrol[j].advancesinspaceresearch.2013,52:2156–2167.参考文献2：penghj,jiangx,chenbs.optimalnonlinearfeedbackcontrolofspacecraftrendezvouswithfinitelowthrustbetweenlibrationorbit[j].nonlineardynamics,2014,76:1611-1632.)由于平动点轨道自身的不稳定性，在设计交会策略时需要充分考虑导航误差、其它行星的引力、测量误差、推力约束等因素对平动点轨道交会的影响。并且国际深空互操作标准草案c-2018组合草案文件(参考文献3：nationalaeronauticsandspaceadministration.internationaldeepspaceinteroperabilitystandardsdraftc-2018combineddraftdocument[eb/ol].)指出深空航天器交会出现的突发性状况包括光学敏感器出现故障。因此如果测量敏感器出现故障不能提供速度测量信息，如何实现平动点轨道航天器的安全精确交会是值得深入研究的问题。现有的方法一般采用数字差分来近似地估计相对位置的导数从而得到相对速度状态，但是平动点轨道相对运动存在扰动和测量噪声，而差分方法具有放大噪声的特性，难以正确地估计出高精度的相对速度状态。因此如何实现既能够高精度地估计原系统的未知状态，而且在对不确定项进行逼近的同时还能抑制噪声是需要解决的一个问题。

低复杂度预设性能控制(lppc)方法从提高系统性能的角度进行控制器设计，可确保跟踪误差收敛到一个预设的任意小区域内，同时使收敛速度和超调量都满足预设的条件。该控制方法可以针对模型具有强不确定性的情形，且控制器的设计仅依赖系统的状态反馈，不需要进行大量的迭代计算(参考文献4：bechliouliscp,rovithakisga.alow-complexityglobalapproximation-freecontrolschemewithprescribedperformanceforunknownpurefeedbacksystems[j].automatica,2014,50(4):1217-1226.)。现有的lppc方法设计稳态变量的约束条件时，需要事先知道初始误差的符号，因此当改变初始值误差时，一旦初始误差的符号发生改变，就需要改变控制参数，实际操作过程繁琐。

因而本发明综合考虑平动点轨道相对运动动力学的强非线性和强不确定性等特点，相对速度难以精确测量或传感器故障造成相对速度测量信息缺失的工况，以及预设性能控制方法需要事先知道初始误差符号的缺陷，提出一种无需相对速度测量信息的平动点轨道航天器交会的自主控制方法。

技术实现要素：

要解决的技术问题

针对在平动点轨道交会中速度测量敏感器出现故障不能提供速度测量信息问题，并预设性能控制方法需要预知初始误差符号的繁琐操作，提出一种仅需相对位置信息和初始误差符号未知的平动点轨道近程交会控制律，用于实现追踪航天器与目标航天器交会任务的高精度实时控制。

技术方案

一种基于三阶积分链观测器的平动点轨道交会无需初始误差符号的预设性能控制方法，其特征在于步骤如下：

步骤1：建立非线性平动点轨道相对动力学模型

圆型限制性三体问题描述两个主天体p1,p2绕着它们共同的质心做圆周运动，分析第三个质量可以忽略的航天器p3在此系统中的运动问题；以p1,p2的质心o为原点，以两主天体p1,p2的连线为x轴，正方向为质量大的主天体指向质量小的主天体，y轴在两个主引力体旋转平面上，z轴与x、y轴满足右手法则；假设质量可以忽略的航天器p3在旋转坐标系o-xyz中的状态为为了便于计算，质量参数定义为μ＝m2/(m1+m2)，其中m1、m2分别为两个主引力体p1、p2的质量，且m2<m1，并令引力常量g，p1、p2之间的距离、旋转角速度、两主天体质量和均为1，则圆型限制性三体问题的运动方程为

其中：ωx,ωy,ωz分别表示势函数ω对x,y,z的偏导，ω、航天器与两主天体p1,p2的距离r1、r2的表达式分别为：

ω＝(x²+y²)/2+(1-μ)/r1+μ/r2，r1＝[(x+μ)²+y²+z²]^1/2，r2＝[(x-1+μ)²+y²+z²]^1/2

假设在质心旋转坐标系中，追踪航天器和目标航天器的状态矢量分别为xc＝[rcvc]^t和xt＝[rtvt]^t，则追踪航天器相对目标航天器的状态矢量为令x1＝[δxδyδz]^t，当考虑推力控制以及扰动时可以得到追踪航天器相对目标航天器的非线性相对运动方程

式中g＝-i3×3，f＝[f1f2f3]^t，具体表达形式为：

分别表示追踪航天器与主天体p1、p2的距离；分别表示目标航天器与主天体p1、p2的距离；则和及k1、k2分别为：

为时变扰动加速度，为控制输入；本发明假设扰动加速度aper是有界未知的，地月系统受太阳引力和太阳光压的量级大约在10^-7和10^-9，即扰动加速度满足不等式

|di|≤di,i＝δx,δy,δz(3)

并假设控制器的执行能力强于干扰上界d＝[dδxdδydδz]^t；

步骤2：建立扰动和不确定性模型

本发明考虑的是深空平动点轨道附近的相对运动问题，空间中的外部扰动一般呈现周期性变化，因此可以表示成周期函数的形式

aper＝[a1sin(ω1t),a2cos(ω2t),a3(sin(ω3t)+cos(ω4t))]^t(4)

其中a1,a2,a3和ω1,ω2,ω3分别是x,y,z方向的扰动幅值及扰动频率；

两航天器相对运动过程中需要不断获取相对运动状态，而光学敏感器测量出的相对信息本身存在一定的误差；这种误差直接影响所需控制量的精度；假设相对导航误差满足均值为零的标准正态分布，则带有导航不确定性的追踪航天器的状态可以表示为

其中是追踪航天器的理想状态，δxc为相对导航误差；

由于航天器特殊的运行环境和复杂的结构，推力器很容易出现失效的情况，直接表现形式就是控制加速度的变化，控制加速度的不确定性可以建模为uc＝lcuc+δuc(6)

其中lc＝[lc1,lc2,lc3]^t表示乘性故障，lci＝1，lci＝0，0<lci<1，分别表示推力器正常、完全失效、部分失效，δuc表示加性故障；

步骤3：设计三阶积分链微分器

本发明利用ticd来估计两个航天器的相对速度，相对运动方程(20)的ticd的形式为

其中是相对运动状态的估计值，是两航天器的相对加速度估计值，τ>0是充分小的摄动参数，τ越小收敛速度越快，精度越高；ci，i＝1,2,3满足hurwitz多项式的参数，根据laplace变换容易得到

本发明设计如下变摄动参数

其中m,为大于零的常数，tmax为最大变化时刻；这样能够保证当0≤t≤tmax时，摄动参数τ的值比较大，从而使得相对运动方程的积分链微分器在初始阶段由于摄动参数比较大，峰值现象可以得到抑制；随着时间的推移，经过初始阶段，τ值变得比较小，从而达到最小值，满足相对运动状态的高精度估计要求；

步骤4：设计平动点轨道交会预设性能控制律

预设性能函数具有两个性质：1)单调递减的正函数；2)当时间趋于无穷时，函数趋于一个任意小的正数；定义如下所示的函数

α(t)＝α⁰/sinh(βt+ω5)+α^∞(10)

式中：α⁰,β,ω5>0为预设性能函数的需要设计的参数；ω5是足够小的数；α^∞>0为预设性能函数的终值，能够保证状态量λ最终收敛于稳定域γλ＝{λ∈r:|λ|<α^∞}中；

显然函数(28)满足预设性能函数的两条性质，因此可以作为预设性能函数；

针对跟踪误差，利用式(28)定义的预设性能函数，可得不等式约束

-δlα(t)<λ(t)<δuα(t)(11)

式中0≤δl,δu≤1是为防止状态量超调而定义的常量，由(28)式看出当ω1→0时α(0)→+∞；因此无论初始误差正负都能保证-δlα(0)<λ(0)<δuα(0)成立；从而当预设性能函数具有式(28)的形式时，放宽了对初始误差已知的限制；

定义广义状态误差量

式中：各个分量λi都是正常数，i＝1,2,3，xd(t)和yd(t)分别表示期望相对轨道的状态和速度，在广义状态误差量中考虑相对轨道速度误差能保证低复杂度预设性能控制器在平动点相对轨道初速度误差很大的情况下航天器仍能很快地沿着期望轨迹飞行；结合预设性能函数(28)和不等式约束(29)式做广义状态量(30)的边界约束

令δl＝[δl1,δl2,δl3]^t，δu＝[δu1,δu2,δu3]^t，由于预设性能函数α(t)＝[α1(t),α2(t),α3(t)]^t是正函数，式(31)也可写成如下形式

对定义如下形式的一一映射函数ψi：

令

则由(32)式可知根据式(33)可构造广义误差状态量的转化状态量

通过式(34)的转化，将有约束不等式的广义误差状态量转化成了不具有约束的状态量θ＝[θ1,θ2,θ3]^t；

ψ＝[ψ1,ψ2,ψ3]^t存在逆映射η(θ)＝ψ^-1(θ(t))，其表达形式为

则转化后状态量的导数如下

式中χ＝diag(α1(t),α2(t),α3(t))，r＝diag(r1,r2,r3)，其分量i＝1,2,3；

针对平动点相对轨道方程(20)，设计预设性能控制器

式中：为可调正常量，q＝diag(q1,q2,q3)，其参数应满足下述不等式

qi>0,i＝1,2,3.和θ^t(0)qθ(0)<1。

有益效果

本发明提出的一种仅需相对位置状态的平动点轨道交会方法，所提出的基于三阶积分链微分器的预设性能控制方法对带有扰动、相对导航误差以及推力器存在故障的情况都能够保证交会末端系统状态满足实际的预设性能，即可以实现追踪航天器与目标航天器的安全精确交会，为未来平动点轨道交会任务提供了一种可行控制策略。

附图说明

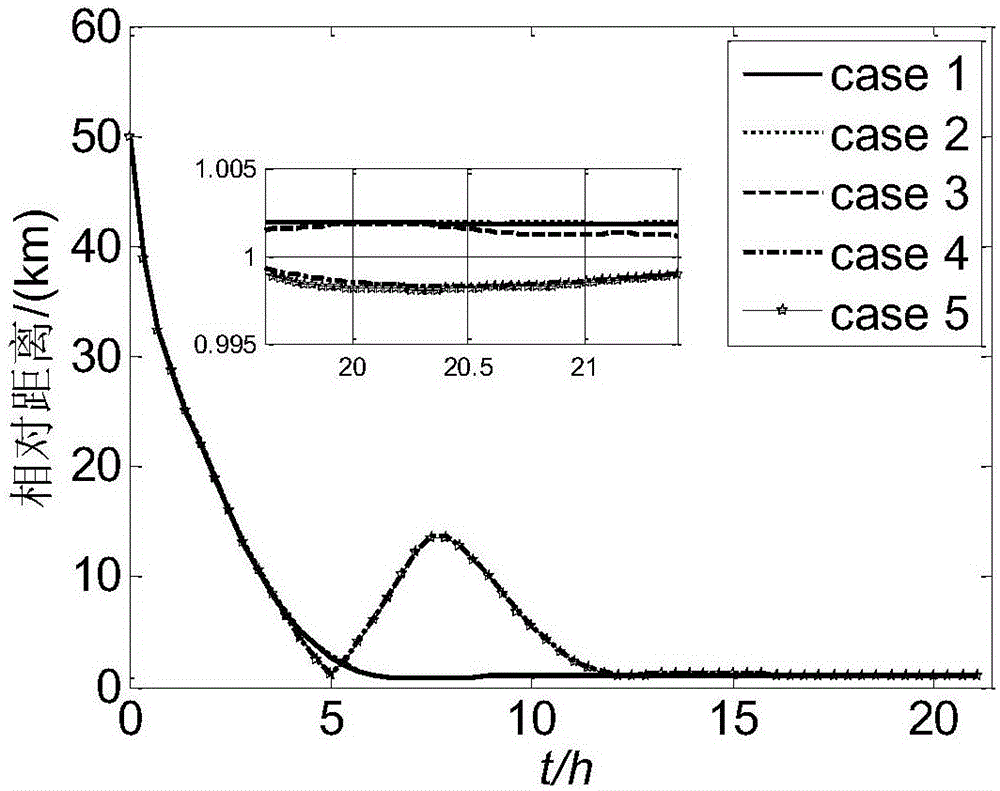
图1相对位置状态变化示意图

图2相对速度状态变化示意图

具体实施方式

现结合实施例、附图对本发明作进一步描述：

本发明基于高阶积分链观测器和预设性能控制，提出了一种仅需相对位置测量信息的平动点轨道自主交会控制方法，并以实例验证了本发明提出方法的有效性。该发明的实施主要包括以下四个步骤：

步骤一：建立非线性平动点轨道相对动力学模型

圆型限制性三体问题描述两个主天体p1,p2绕着它们共同的质心做圆周运动，分析第三个质量可以忽略的航天器p3在此系统中的运动问题。以p1,p2的质心o为原点，以两主天体p1,p2的连线为x轴，正方向为质量大的主天体指向质量小的主天体，y轴在两个主引力体旋转平面上，z轴与x、y轴满足右手法则。假设质量可以忽略的航天器p3在旋转坐标系o-xyz中的状态为为了便于计算，质量参数定义为μ＝m2/(m1+m2)，其中m1、m2(m2<m1)分别为两个主引力体p1、p2的质量，并令引力常量g，p1、p2之间的距离、旋转角速度、两主天体质量和均为1，则圆型限制性三体问题的运动方程为

其中：ωx,ωy,ωz分别表示势函数ω对x,y,z的偏导，ω、航天器与两主天体p1、p2的距离r1、r2的表达式分别为：

ω＝(x²+y²)/2+(1-μ)/r1+μ/r2r1＝[(x+μ)²+y²+z²]^1/2,r2＝[(x-1+μ)²+y²+z²]^1/2。

假设在质心旋转坐标系中，追踪航天器和目标航天器的状态矢量分别为xc＝[rcvc]^t和xt＝[rtvt]^t，则追踪航天器相对目标航天器的状态矢量为令x1＝[δxδyδz]^t，当考虑推力控制以及扰动时可以得到追踪航天器相对目标航天器的非线性相对运动方程

式中g＝-i3×3，f＝[f1f2f3]^t，具体表达形式为：

分别表示追踪航天器与主天体p1、p2的距离；分别表示目标航天器与主天体p1、p2的距离；则和及k1、k2分别为：

为时变扰动加速度，包含直接、间接引力以及外部干扰等，为控制输入。本发明假设扰动加速度aper是有界未知的，这种假设是合理的：地月系统受太阳引力和太阳光压的量级大约在10^-7和10^-9，即扰动加速度满足不等式

|di|≤di,i＝δx,δy,δz(21)

并假设控制器的执行能力强于干扰上界d＝[dδxdδydδz]^t。

步骤二：建立扰动和不确定性模型

本发明考虑的是深空平动点轨道附近的相对运动问题，空间中的外部扰动一般呈现周期性变化，因此可以表示成周期函数的形式

aper＝[a1sin(ω1t),a2cos(ω2t),a3(sin(ω3t)+cos(ω4t))]^t(22)

其中a1,a2,a3和ω1,ω2,ω3分别是x,y,z方向的扰动幅值及扰动频率。

两航天器相对运动过程中需要不断获取相对运动状态，而光学敏感器测量出的相对信息本身存在一定的误差。这种误差直接影响所需控制量的精度。假设相对导航误差满足均值为零的标准正态分布，则带有导航不确定性的追踪航天器的状态可以表示为

其中是追踪航天器的理想状态，δxc为相对导航误差。

由于航天器特殊的运行环境和复杂的结构，推力器很容易出现失效的情况，直接表现形式就是控制加速度的变化，控制加速度的不确定性可以建模为

uc＝lcuc+δuc(24)

其中lc＝[lc1,lc2,lc3]^t表示乘性故障，lci＝1,lci＝0,0<lci<1，分别表示推力器正常、完全失效、部分失效，δuc表示加性故障。

步骤三：设计三阶积分链微分器

本发明利用ticd来估计两个航天器的相对速度。相对运动方程(20)的ticd的形式为

其中是相对运动状态的估计值，是两航天器的相对加速度估计值，τ>0是充分小的摄动参数，τ越小收敛速度越快，精度越高。ci(i＝1,2,3)满足hurwitz多项式的参数，根据laplace变换容易得到

即使存在模型不确定、噪声及外界扰动，ticd仍能有效地估计航天器的相对速度和相对加速度，由于高精度的要求，τ取的越小越好，但是过小的τ会使得由方程(25)所得到的相对速度很容易会出现很大的超调。如果将由方程(25)得到的相对速度用于系统的反馈控制，由于强烈的震荡，会使整个闭环系统发散。因此本发明设计如下变摄动参数

其中m,为大于零的常数，tmax为最大变化时刻。这样能够保证当0≤t≤tmax时，摄动参数τ的值比较大，从而使得相对运动方程的积分链微分器在初始阶段由于摄动参数比较大，峰值现象可以得到抑制。随着时间的推移，经过初始阶段，τ值变得比较小，从而达到最小值，满足相对运动状态的高精度估计要求。

步骤四：平动点轨道交会预设性能控制律设计

预设性能函数具有两个性质：1)单调递减的正函数；2)当时间趋于无穷时，函数趋于一个任意小的正数。定义如下所示的函数

α(t)＝α⁰/sinh(βt+ω5)+α^∞(28)

式中：α⁰,β,ω5>0为预设性能函数的需要设计的参数；ω5是足够小的数；α^∞>0为预设性能函数的终值，能够保证状态量λ最终收敛于稳定域

γλ＝{λ∈r:|λ|<α^∞}

中。显然函数(28)满足预设性能函数的两条性质，因此可以作为预设性能函数。

针对跟踪误差，利用式(28)定义的预设性能函数，可得不等式约束

-δlα(t)<λ(t)<δuα(t)(29)

式中0≤δl,δu≤1是为防止状态量超调而定义的常量，由(28)式看出当ω1→0时α(0)→+∞。因此无论初始误差正负都能保证

-δlα(0)<λ(0)<δuα(0)

成立。从而当预设性能函数具有式(28)的形式时，放宽了对初始误差已知的限制。

定义广义状态误差量

式中：各个分量λi(i＝1,2,3)都是正常数，xd(t)和yd(t)分别表示期望相对轨道的状态和速度，在广义状态误差量中考虑相对轨道速度误差能保证低复杂度预设性能控制器在平动点相对轨道初速度误差很大的情况下航天器仍能很快地沿着期望轨迹飞行。结合预设性能函数(28)和不等式约束(29)式做广义状态量(30)的边界约束

令δl＝[δl1,δl2,δl3]^t，δu＝[δu1,δu2,δu3]^t，由于预设性能函数α(t)＝[α1(t),α2(t),α3(t)]^t是正函数，式(31)也可写成如下形式

对定义如下形式的一一映射函数ψi：

令

则由(32)式可知根据式(33)可构造广义误差状态量的转化状态量

通过式(34)的转化，将有约束不等式的广义误差状态量e转化成了不具有约束的状态量θ＝[θ1,θ2,θ3]^t。

ψ＝[ψ1,ψ2,ψ3]^t存在逆映射η(θ)＝ψ^-1(θ(t))，其表达形式为

则转化后状态量的导数如下

式中χ＝diag(α1(t),α2(t),α3(t))，r＝diag(r1,r2,r3)，其分量ri(i＝1,2,3)为

针对平动点相对轨道方程(20)，设计预设性能控制器

式中：为可调正常量，q＝diag(q1,q2,q3)，其参数应满足下述不等式

qi>0,i＝1,2,3.和θ^t(0)qθ(0)<1

本发明以振幅az＝10000km的地-月l1halo轨道为目标航天器所在轨道为例来验证本发明的有效性和鲁棒性。假设追踪航天器和目标航天器的初始相对位置和速度状态分别为[50；0；0]km和[-10；5；6]m/s，最终期望的两航天器相对位置和速度状态为[1；0；0]km及[0；0；0]m/s。外部扰动参数设计为a1＝a2＝10^-7,a3＝0，即外部扰动的幅值选取的是太阳引力和太阳光压的最大值，ω1＝ω2＝π/900。两航天器相对位置导航精度如表1所示，失效推力器所提供的控制加速度的形式如方程(37)所示。积分链微分器的设计参数为c1＝1；c1＝2；c1＝3；m＝2000；控制器设计参数如表2所示。

通过五种工况对本发明所提出的交会控制方法进行数值仿真验证，工况一(case1)：假设扰动为零，也不存在导航和制导误差，这是一种理想状态，用来验证本发明所提方法的有效性；工况二(case2)：只考虑扰动；工况三(case3)：只考虑导航误差；工况四(case4)：制导不确定性；工况五(case5)同时考虑导航误差、扰动以及制导不确定性。后四种工况用来验证本文方法的鲁棒性。

图1和图2分别为两个航天器在三阶积分链微分器-预设性能控制器下的相对位置和相对速度的变化曲线，从图中可以看出，相对位置和相对速度可以收敛到期望交会状态的很小邻域内。即表明，可以实现追踪航天器与目标航天器的近程交会任务。相对于理想状态，当推力器存在故障时，系统状态收敛速度比较慢，而扰动和相对导航误差对其收敛速度几乎没有影响。不论哪种不确定性，交会状态的末端误差的量级相同。

表1两航天器相对导航误差

表2预设性能函数和控制器参数