飞行器及其飞行控制方法和装置与流程
本申请属于空中抵近作业与飞控技术领域，尤其涉及一种飞行器及其飞行控制方法和装置。
背景技术：
作为一种飞行器，无人机的相关研究已经成为当今社会的一个研究热点。其中，利用空中无人机及相关装备代替人执行空中作业任务是未来的发展趋势。空中无人机搭载作业设备代替人去完成空中作业任务，能够减少经济成本、减少劳动强度以及降低执行工作任务的安全风险。
未来的空中作业中，不仅要求无人机能执行远距离拍照及侦察等工作，还要求其能满足修复高空设备或者执行高空救援等需求，这些需求要求无人机能够近距离靠近壁面，或者与环境进行交互接触式作业，而能安全地抵近壁面飞行(主要是指抵近壁面悬停以执行作业的工况)又是实现无人机与壁面接触工作的前提基础。
目前的大多数无人机不能实现抵近壁面飞行，如目前主流的无人机结构形式大多为开放旋翼式的，开放旋翼式结构的无人机一般工作时会远离环境中的各种壁面，在空间紧凑且复杂的环境下飞行或需要抵近壁面进行作业时，一般不能胜任；而少数关于无人机对抵近壁面的研究，也只是笼统地将无人机与壁面之间的气动效应也即壁面效应作为一个外部扰动，并利用相关控制算法尽可能地消除扰动所带来的不利影响，如，通过自适应神经网络算法估计扰动大小并调节控制器的控制律，使得无人机姿态依旧能稳定悬停,以维持无人机近壁面工作的稳定性。然而，这仅从补偿外部扰动角度对无人机与壁面之间的气动效应进行了一定补偿，难以完全消除扰动所带来的不利影响，尤其是在无人机与壁面距离很小时，这些干扰还是会影响无人机的工作性能，从而难以完全保障无人机抵近壁面时的稳定性，相应导致无人机在抵近壁面作业时仍存在安全隐患。
由此，目前的无人机等飞行器要么无法抵近壁面飞行，要么仅将无人机与壁面产生的壁面效应简单作为一个外部扰动加以补偿，难以较高程度地保障无人机抵近壁面时的稳定性，仍存在安全隐患。
技术实现要素：
有鉴于此，本申请的目的在于提供一种飞行器及其飞行控制方法和装置，通过考虑壁面效应对整机模型的影响将壁面效应纳入飞行器模型的构建中，来确定整机系统稳定前提下飞行器与壁面的最小安全距离，最终基于该最小安全距离保障飞行器在空中抵近壁面飞行时的稳定性及安全性能。
一种飞行器的飞行控制方法，所述飞行器为涵道式飞行器；所述方法包括：
确定壁面效应下飞行器的合力矢量及合力矩矢量与飞行器至壁面的距离之间的关联关系；
基于所述关联关系构建飞行器有壁面效应时的第一动力学模型；所述第一动力学模型中包括基于所述距离表达的所述合力矢量及所述合力矩矢量；
基于所述第一动力学模型确定飞行器有壁面效应时的第一空间状态方程；所述第一空间状态方程的系统矩阵与控制矩阵中包括所述距离；
利用一给定的目标反馈控制器及所述第一空间状态方程的系统矩阵与控制矩阵，构建飞行器有壁面效应时的第一闭环系统；所述目标反馈控制器为能使飞行器无壁面效应时的第二闭环系统维持稳定的反馈控制器；
确定能使所述第一闭环系统维持稳定的所述距离的最小值，得到飞行器至壁面的最小安全距离；
基于所述最小安全距离，控制飞行器的飞行。
上述方法，优选的，飞行器至壁面的距离为飞行器旋翼中心到壁面的距离dwe，所述合力矢量包括：飞行器在有壁面效应悬停工况时的系统总升力矢量与重力矢量；所述合力矩矢量包括：飞行器在有壁面效应悬停工况时的反扭矩矢量与倾转力矩矢量；
所述确定壁面效应下飞行器的合力矢量及合力矩矢量与飞行器至壁面的距离之间的关联关系，包括：
确定飞行器的系统总升力矢量与距离比dwe/r之间的关联关系；
确定飞行器的反扭矩矢量与距离比dwe/r之间的关联关系；
确定飞行器的倾转力矩矢量与距离比dwe/r之间的关联关系；
基于系统总升力矢量、反扭矩矢量、倾转力矩矢量分别与距离比dwe/r之间的关联关系，确定系统总升力矢量、反扭矩矢量、倾转力矩矢量分别与距离dwe之间的关联关系；
其中，所述距离比dwe/r为飞行器旋翼中心到壁面的距离dwe与飞行器螺旋桨半径r的比值。
上述方法，优选的，在所述基于所述关联关系构建飞行器有壁面效应时的第一动力学模型之前，还包括：
构建飞行器无壁面效应时的第二动力学模型；所述第二动力学模型的输入包括除去重力外飞行器所受到的合外力向量fb、飞行器整体所受到的气动力矩向量mb及飞行器重力fg，输出包括飞行器机体的线速度向量、角速度向量及欧拉角向量，飞行器的系统总升力矢量为所述合外力向量fb在机体z轴方向上的分力，飞行器的反扭矩矢量为所述气动力矩向量mb绕所述z轴的力矩量。
上述方法，优选的，所述基于所述关联关系构建飞行器有壁面效应时的第一动力学模型，包括：
基于所述关联关系确定对所述系统总升力矢量进行修正的修正因子α与对所述反扭矩矢量进行修正的修正因子β，并确定所述倾转力矩矢量的表达式；所述修正因子α、β及所述倾转力矩矢量的表达式中包括所述距离dwe；
利用所述修正因子α对所述第二动力学模型中的合外力向量fb在机体z轴方向上的分力进行修正；利用所述修正因子β对所述第二动力学模型中的气动力矩向量mb绕所述z轴的力矩量进行修正；并向所述第二动力学模型的输入中引入所述倾转力矩矢量，得到飞行器有壁面效应时的第一动力学模型。
上述方法，优选的，所述第一动力学模型为一非线性系统；所述基于所述第一动力学模型确定飞行器有壁面效应时的第一空间状态方程，包括：
在所述第一动力学模型的系统平衡点处，将所述第一动力学模型线性化为一线性系统；
基于预定辨识技术，确定所述第一动力学模型线性化后的线性系统对应的状态空间方程，得到飞行器有壁面效应时的第一状态空间方程。
上述方法，优选的，所述第二动力学模型为一非线性系统；所述利用一给定的目标反馈控制器及所述第一空间状态方程的系统矩阵与控制矩阵，构建飞行器有壁面效应时的第一闭环系统，包括：
在所述第二动力学模型的系统平衡点处，将所述第二动力学模型线性化为一线性系统；
基于预定辨识技术，确定所述第二动力学模型线性化后的线性系统对应的状态空间方程，得到飞行器无壁面效应时的第二状态空间方程；
基于所述第二状态空间方程，确定无壁面效应时飞行器的第二闭环系统；
确定能使飞行器无壁面效应时的所述第二闭环系统维持稳定的目标反馈控制器；
利用所述目标反馈控制器及所述第一空间状态方程的系统矩阵与控制矩阵，构建飞行器有壁面效应时的第一闭环系统。
一种飞行器的飞行控制装置，所述飞行器为涵道式飞行器；所述装置包括：
第一确定单元，用于确定壁面效应下飞行器的合力矢量及合力矩矢量与飞行器至壁面的距离之间的关联关系；
第一构建单元，用于基于所述关联关系构建飞行器有壁面效应时的第一动力学模型；所述第一动力学模型中包括基于所述距离表达的所述合力矢量及所述合力矩矢量；
第二确定单元，用于基于所述第一动力学模型确定飞行器有壁面效应时的第一空间状态方程；所述第一空间状态方程的系统矩阵与控制矩阵中包括所述距离；
第二构建单元，用于利用一给定的目标反馈控制器及所述第一空间状态方程的系统矩阵与控制矩阵，构建飞行器有壁面效应时的第一闭环系统；所述目标反馈控制器为能使飞行器无壁面效应时的第二闭环系统维持稳定的反馈控制器；
第三确定单元，用于确定能使所述第一闭环系统维持稳定的所述距离的最小值，得到飞行器至壁面的最小安全距离；
控制单元，用于基于所述最小安全距离，控制飞行器的飞行。
上述装置，优选的，飞行器至壁面的距离为飞行器旋翼中心到壁面的距离dwe，所述合力矢量包括：飞行器在有壁面效应悬停工况时的系统总升力矢量与重力矢量；所述合力矩矢量包括：飞行器在有壁面效应悬停工况时的反扭矩矢量与倾转力矩矢量；
所述第一确定单元，具体用于：
确定飞行器的系统总升力矢量与距离比dwe/r之间的关联关系；
确定飞行器的反扭矩矢量与距离比dwe/r之间的关联关系；
确定飞行器的倾转力矩矢量与距离比dwe/r之间的关联关系；
基于系统总升力矢量、反扭矩矢量、倾转力矩矢量分别与距离比dwe/r之间的关联关系，确定系统总升力矢量、反扭矩矢量、倾转力矩矢量分别与距离dwe之间的关联关系；
其中，所述距离比dwe/r为飞行器旋翼中心到壁面的距离dwe与飞行器螺旋桨半径r的比值。
上述装置，优选的，还包括：
第三构建单元，用于在所述第一构建单元基于所述关联关系构建飞行器有壁面效应时的第一动力学模型之前，构建飞行器无壁面效应时的第二动力学模型；所述第二动力学模型的输入包括除去重力外飞行器所受到的合外力向量fb、飞行器整体所受到的气动力矩向量mb及飞行器重力fg，输出包括飞行器机体的线速度向量、角速度向量及欧拉角向量，飞行器的系统总升力矢量为所述合外力向量fb在机体z轴方向上的分力，飞行器的反扭矩矢量为所述气动力矩向量mb绕所述z轴的力矩量。
上述装置，优选的，所述第一构建单元，具体用于：
基于所述关联关系确定对所述系统总升力矢量进行修正的修正因子α与对所述反扭矩矢量进行修正的修正因子β，并确定所述倾转力矩矢量的表达式；所述修正因子α、β及所述倾转力矩矢量的表达式中包括所述距离dwe；
利用所述修正因子α对所述第二动力学模型中的合外力向量fb在机体z轴方向上的分力进行修正；利用所述修正因子β对所述第二动力学模型中的气动力矩向量mb绕所述z轴的力矩量进行修正；并向所述第二动力学模型的输入中引入所述倾转力矩，得到飞行器有壁面效应时的第一动力学模型。
上述装置，优选的，所述第一动力学模型与所述第二动力学模型分别为一非线性系统；
所述第二确定单元，具体用于：
在所述第一动力学模型的系统平衡点处，将所述第一动力学模型线性化为一线性系统；
基于预定辨识技术，确定所述第一动力学模型线性化后的线性系统对应的状态空间方程，得到飞行器有壁面效应时的第一状态空间方程；
所述第二构建单元，具体用于：
在所述第二动力学模型的系统平衡点处，将所述第二动力学模型线性化为一线性系统；
基于预定辨识技术，确定所述第二动力学模型线性化后的线性系统对应的状态空间方程，得到飞行器无壁面效应时的第二状态空间方程；
基于所述第二状态空间方程，确定无壁面效应时飞行器的第二闭环系统；
确定能使飞行器无壁面效应时的所述第二闭环系统维持稳定的目标反馈控制器；
利用所述目标反馈控制器及所述第一空间状态方程的系统矩阵与控制矩阵，构建飞行器有壁面效应时的第一闭环系统。
一种飞行器，包括：机身及至少两个涵道螺旋桨系统；
还包括：
控制器，用于基于如上所述的飞行控制方法中的所述最小安全距离对所述飞行器进行飞行控制；或者，接收外部控制信号，并基于该控制信号对飞行器进行飞行控制，该控制信号为基于如上所述的飞行控制方法中的最小安全距离所生成的信号。
由以上方案可知，本申请提供了一种飞行器及其飞行控制方法和装置，该飞行器为涵道式飞行器，相比于开放旋翼式飞行器，涵道式飞行器可以满足高空抵近飞行的需求，且相比于现有方案，本申请研究了飞行器抵近壁面时所产生的壁面效应与飞行器距离壁面间距的关系，并将其所带来的影响纳入到飞行器模型的构建中一起考虑，通过分析得到飞行器至壁面的距离和系统稳定性的关系，进而转化得到一个允许抵近的最小安全距离，也即整机系统稳定前提下飞行器与壁面的最小安全距离，而基于该考虑了壁面效应所得的最小安全距离对飞行器进行飞行控制，显然可使得飞行器抵近壁面飞行(主要是指抵近壁面悬停以执行作业的工况)时的稳定性及安全性得以提升。
附图说明
为了更清楚地说明本申请实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本申请的实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据提供的附图获得其他的附图。
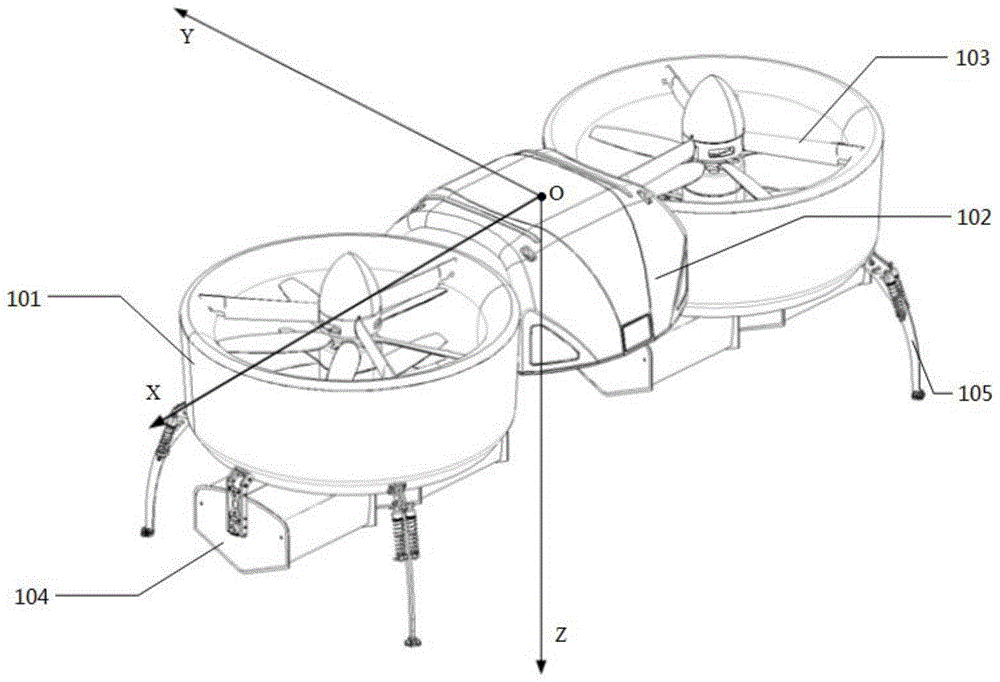
图1是本申请可选实施例提供的共轴反桨双涵道无人机的结构示意图；
图2是本申请可选实施例提供的飞行器的飞行控制方法的流程示意图；
图3是本申请可选实施例提供的涵道式无人机的壁面效应流线示意图；
图4(a)是本申请可选实施例提供的不同距离比时的总升力示意图；
图4(b)是本申请可选实施例提供的不同距离比时的反扭矩示意图；
图4(c)是本申请可选实施例提供的不同距离比时的倾转力矩示意图；
图5是本申请可选实施例提供的涵道式无人机未考虑壁面效应时的动力学模型结构图；
图6是本申请可选实施例提供的涵道式无人机考虑了壁面效应时的动力学模型结构图；
图7是本申请可选实施例提供的飞行器的飞行控制装置的一种结构示意图；
图8是本申请可选实施例提供的飞行器的飞行控制装置的另一种结构示意图；
图9本申请可选实施例提供的飞行器的结构示意图。
具体实施方式
下面将结合本申请实施例中的附图，对本申请实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本申请一部分实施例，而不是全部的实施例。基于本申请中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本申请保护的范围。
本申请公开了一种飞行器及其飞行控制方法和装置，通过考虑壁面效应对整机模型的影响将壁面效应纳入飞行器模型的构建中，来确定整机系统稳定前提下飞行器与壁面的最小安全距离，最终基于该最小安全距离保障飞行器在空中抵近壁面飞行时的稳定性及安全性能。
本申请中的所述飞行器，主要是指可以搭载作业设备代替人去完成空中作业任务的无人机，目前，主流的无人机结构形式大多为开放旋翼式的，开放旋翼结构无人机一般工作时会远离环境中的各种壁面，在空间紧凑且复杂的环境下飞行或需要抵近壁面进行作业时，一般不能胜任。与开放旋翼式无人机相比，涵道式无人机可以在更危险、更复杂、及未知的环境中工作。由于涵道的存在，内部的桨叶可以避免与外界直接接触，在发生意外时，桨叶不会直接弹射到人，这也使得其安全性能更强。此外，由于涵道唇口中气流的作用，在相同的桨叶尺寸下，涵道式无人机产生的推力比开放旋翼式的更多。且涵道式无人空中作业平台因其结构紧凑、载荷大、安全性高的特点，可以在复杂、狭窄环境中代替人类进行作业任务。
鉴于涵道式无人机的上述优势，本申请主要针对涵道式无人机，研究其在壁面效应影响下能确保系统稳定性、安全性的安全飞行范围，进而对其进行飞行控制。
可选地，所述涵道式无人机可以是共轴反桨的双涵道无人机，其在执行高空作业时抵近的壁面一般而言为竖直的壁面或墙壁。为便于理解，以下首先对该共轴反桨的双涵道无人机的组成结构及各组成部分的功能做简单介绍。
如图1所示，该共轴反桨的双涵道无人机主要由两个涵道螺旋桨系统101以及机身102构成。两个涵道螺旋桨系统101采用纵列形式，且对称设置于机身102两侧。涵道螺旋桨系统101内设置两个结构、大小相同且共轴设置的螺旋桨：上桨和下桨。上下桨旋转方向相反，可以相互抵消旋转过程中产生的不平衡力矩。涵道螺旋桨系统101中还设有驱动电机，螺旋桨与电机相连，通过电机输出旋转动力，电机支架103用于固定电机。机身102内设置电池、飞控系统等。在两个涵道下方各固定连接一个控制舵104，控制舵104具有气动舵面，用于产生滚转方向的控制力矩。整个双涵道无人机的升力由前后两个涵道内的四个螺旋桨提供，俯仰和横摆力矩由前后涵道中的螺旋桨之间的速度差提供，通过前后涵道中螺旋桨的转速差产生俯仰方向的力矩以控制机体的俯仰通道，通过舵面偏转产生滚转方向的力矩控制机体的滚转通道，通过每个涵道内上下两个螺旋桨旋向相反产生的扭矩差控制机体的偏航通道，进而实现机体的姿态控制。除此之外，还可以包括起落架105。
涵道式无人机的坐标系o-xyz请参阅图1，由于涵道式无人机抵近壁面飞行时，其作业执行部件一般在机身中间，故此涵道一般为其y轴方向或y轴负方向朝向于壁面。
本申请主要针对上述的涵道式无人机，研究在悬停飞行工况下，在受到壁面效应的影响时，无人机至壁面的距离与系统自身稳定性的关系，进而在此基础上，通过将壁面效应纳入飞行器模型的构建中，来确定整机系统稳定前提下无人机与壁面之间的最小安全距离，进而达到对无人机的进行安全飞控、保障无人机在抵近壁面作业时的稳定性及安全性的目的。
参阅图2，为本申请针对涵道式无人机，提供的一种飞行器的飞行控制方法的流程示意图，如图2所示，该飞行控制方法可以包括以下处理过程：
步骤201、确定壁面效应下飞行器的合力矢量及合力矩矢量与飞行器至壁面的距离之间的关联关系。
发明人经研究发现，由于共轴反桨涵道式无人机靠近竖直壁面悬停时，壁面会阻止气体的自由运动，使得靠近壁面一侧的涵道唇口处的气流减速，该处的静压升高，最终形成一个不平衡力矩，驱使涵道唇口向竖直壁面一侧倾转，壁面效应流线如图3所示，其中，301表示墙壁，302表示涵道壁面，303表示螺旋桨上桨叶，304表示螺旋桨下桨叶，305表示涵道壁面。形成的所述不平衡力矩即为倾转力矩，由于当该力矩过大时会严重影响涵道式无人机的稳定性，使无人机向壁面倾转，进而导致十分明显的“碰壁现象”，因此其在壁面效应对整机带来的影响的分析中不容忽视。
由此，本申请实施例中，在构建有壁面效应时的第一动力学模型并基于该模型对飞行器进行飞行控制时，会纳入对飞行器在有壁面效应悬停工况时的倾转力矩矢量的考虑，除此之外，还会考虑飞行器在有壁面效应悬停工况时的系统总升力矢量与重力矢量、飞行器在有壁面效应悬停工况时的反扭矩矢量等因素。
从而，本步骤201中，所述合力矢量可以包括但不限于：飞行器在有壁面效应悬停工况时的系统总升力矢量与重力矢量；所述合力矩矢量可以包括但不限于：飞行器在有壁面效应悬停工况时的反扭矩矢量与倾转力矩矢量。另外，本实施例具体采用飞行器旋翼中心到壁面的距离dwe来表示飞行器至壁面的距离。
发明人通过cfd(computationalfluiddynamics，计算流体动力学)仿真实验，分析了当dwe/r为不同比值时的无人机系统总拉力矢量、反扭矩矢量和倾转力矩矢量的数据，其中dwe为无人机旋翼中心到竖直壁面的距离，r为螺旋桨半径，以此得到飞行器的系统总升力矢量、反扭矩矢量、倾转力矩矢量分别与距离比dwe/r之间的关联关系，仿真实验中所得的系统总升力矢量、反扭矩矢量、倾转力矩矢量分别与距离比dwe/r之间的关系，具体可分别参阅图4(a)、图4(b)、图4(c)所示。
在此基础上，可转换得到涵道式无人机至壁面的不同距离dwe下，无人机系统的总升力矢量、反扭矩矢量及其倾转力矩矢量的数据，将这些数据通过最小二乘法进行拟合，可以得到无人机至壁面的距离与系统总升力矢量、反扭矩矢量和倾转力矩矢量的相关表达式。
步骤202、基于所述关联关系构建飞行器有壁面效应时的第一动力学模型；所述第一动力学模型中包括基于所述距离表达的所述合力矢量及所述合力矩矢量。
本申请实施例中，该有壁面效应时的第一动力学模型，为在无壁面效应时的第二动力学模型的基础上所构建的模型，从而在构建该无壁面效应时的第一动力学模型之前，可预先构建飞行器无壁面效应时的第二动力学模型。
在不考虑壁面效应的情况下，可以根据叶素理论和动量理论推导双涵道式无人机的系统模型方程，也即，无壁面效应时的第二动力学模型，并建立无壁面效应时系统的动力学模型结构图，该动力学模型结构图具体可参阅图5，其中，ucol，ulat，ulon与uped分别表示油门(高度)、横向(滚转)、纵向(俯仰)、航向(偏航)通道的归一化控制量。无人机的相应执行机构输入这些量后，输出的是给涵道系统的旋翼转速及舵面角度，基于该旋翼转速及舵面角度，共轴反桨系统会产生相对应的合外力向量fb及气动力矩向量mb，其中，fb具体表示除去重力外无人机所受到的合外力向量，mb具体表示无人机整体所受到的气动力矩向量。
根据系统的合外力向量fb、气动力矩向量mb及飞行器重力fg，由牛顿欧拉方程可推导出系统的非线性动力学方程，从而得到非线性动力学系统，该系统也即为无壁面效应时无人机的第二动力学模型。其中，该第二动力学模型的输入包括除去重力外飞行器所受到的合外力向量fb、飞行器整体所受到的气动力矩向量mb及飞行器重力fg，输出包括无人机机体三个方向线速度向量(u,v,w)t、机体三个方向角速度向量(p,q,r)t及机体欧拉角向量(φ,θ,ψ)t。
需要说明的是，无人机的系统总升力矢量为所述合外力向量fb在机体z轴方向上的分力，反扭矩矢量为所述气动力矩向量mb绕所述z轴的力矩量。
在此基础上，构建飞行器有壁面效应时的第一动力学模型，可通过如下处理过程实现：
1)基于所述关联关系确定对所述系统总升力矢量进行修正的修正因子α与对所述反扭矩矢量进行修正的修正因子β，并确定所述倾转力矩矢量的表达式；
在无人机周围没有壁面时，涵道自身并没有壁面效应，这就等同于在系统建模时，由于涵道壁面与壁面距离足够远，壁面效应所带来的影响非常小，可以忽略不计故没有计入模型之中，而在有约束环境时，壁面效应带来的影响需要在建模时一起考虑。
考虑到壁面效应带来的影响，本实施例具体对无约束环境时的系统总升力矢量与反扭矩矢量进行修正，也即对无壁面效应时的第二动力学模型中的系统总升力矢量和反扭矩矢量进行修正，以此使得将壁面效应带来的影响纳入无人机整机模型的构建中。其中，为了实现对系统总升力矢量与反扭矩矢量的修正，需分别确定一个关于力和力矩的修正因子。
系统有壁面效应时对系统总升力矢量进行修正的修正因子α，与上述的距离比值dwe/r有关，可基于不同距离比值(有壁面效应)时的系统总升力矢量与无约束环境下系统总升力矢量之比而得到，系统有壁面效应时对反扭矩矢量进行修正的修正因子β，与α相似，可基于不同距离比值(有壁面效应)时的系统反扭矩矢量与无约束环境下系统反扭矩矢量之比而得。同时，倾转力矩矢量my也与该距离比值有一定的关系，可由距离比值表示。
3)利用所述修正因子α对所述第二动力学模型中的合外力向量fb在机体z轴方向上的分力进行修正；利用所述修正因子β对所述第二动力学模型中的气动力矩向量mb绕所述z轴的力矩量进行修正；并向所述第二动力学模型的输入中引入所述倾转力矩矢量，得到飞行器有壁面效应时的第一动力学模型。
在确定出上述的修正因子α、β及倾转力矩矢量my的基础上，可进一步利用修正因子α对无壁面效应时的第二动力学模型的系统总升力矢量(fb在机体z轴方向上的分力)进行修正，利用修正因子β对无壁面效应时的第二动力学模型的反扭矩矢量(mb绕所述z轴的力矩量)进行修正，而对于倾转力矩矢量my，在进行有壁面效应时无人机的第一动力学模型的建模中，可向模型中单独加入该倾转力矩矢量my，最终得到有壁面效应时无人机的第一动力学模型，该有壁面效应时的第一动力学模型的模型结构图具体可参阅图6。
其中，在图6中，
l为系统总升力修正矩阵，n为系统反扭矩修正矩阵。
有壁面效应时无人机的第一动力学模型，与无壁面效应时无人机的第二动力学模型相比，将壁面效应带来的力与力矩的变化以及倾转力矩纳入了模型中，最终得到了含有壁面效应的非线性动力学系统。
步骤203、基于所述第一动力学模型确定飞行器有壁面效应时的第一空间状态方程；所述第一空间状态方程的系统矩阵与控制矩阵中包括所述距离。
其中，可根据非线性动力学系统线性化理论，在所述第一动力学模型的系统平衡点处，将所述第一动力学模型简化处理为一线性系统，并基于相关辨识技术，如ukf(unscentedkalmanfilter，无迹卡尔曼滤波)参数估计等，确定所述第一动力学模型线性化后的线性系统对应的状态空间方程，得到飞行器有壁面效应时的第一状态空间方程。
系统有壁面效应时的第一状态空间方程可表示为：
其中，x为状态空间下的9维系统状态向量，x＝[u,v,w,p,q,r,φ,θ,ψ]t，如上文所述，其中(u,v,w)t为机体三个方向的线速度向量，(p,q,r)t为机体三个方向的角速度向量，(φ,θ,ψ)t为机体欧拉角向量。u为归一化后的控制输入向量，u＝[ucol,ulat,ulon,uped]t，其中ucol，ulat，ulon与uped分别对应油门(高度)、横向(滚转)、纵向(俯仰)、航向(偏航)通道的归一化控制量；a′为有壁面效应时的系统矩阵，b′为有壁面效应时的控制矩阵，a′、b′中包括飞行器旋翼中心到壁面的距离dwe。
步骤204、利用一给定的目标反馈控制器及所述第一空间状态方程的系统矩阵与控制矩阵，构建飞行器有壁面效应时的第一闭环系统；所述目标反馈控制器为能使飞行器无壁面效应时的第二闭环系统维持稳定的反馈控制器。
以下先说明确定所述目标反馈控制器的过程。
首先，可根据非线性动力学系统线性化理论，在所述第二动力学模型的系统平衡点处，将所述第二动力学模型简化处理为一线性系统，并基于相关辨识技术，如ukf参数估计等，确定所述第二动力学模型线性化后的线性系统对应的状态空间方程，得到飞行器无壁面效应时的第二状态空间方程。
系统无壁面效应时的第二状态空间方程可表示为：
该式中，a为无壁面效应时的系统矩阵，b为无壁面效应时的控制矩阵；与a′、b′相区别，a、b中不包括飞行器旋翼中心到壁面的距离dwe。x、u表示的含义可参阅上文的介绍。
之后，可进一步根据无壁面效应时的第二状态空间方程中的系统矩阵a、控制矩阵b确定无人机无壁面效应时的开环系统与闭环系统。
无壁面效应时的开环系统的表达式如下：
g(s)＝c(si-a)-1b+d；
该式中，s为复变量，i为单位矩阵，c、d为常量，优选地，c＝eye(9)d＝zeros(9,4)。
无壁面效应时的闭环系统(即所述第二闭环系统)的表达式如下：
其中，涵道式无人机是开环不稳定的系统，需要反馈控制器进行调节以保证无人机的稳定，由此，可以设计一能使无人机在无壁面效应时其闭环系统稳定可用的反馈控制器，如，lqr控制器，控制器矩阵为k，该能使飞行器无壁面效应时的闭环系统维持稳定的控制器，即可以作为所述给定的目标反馈控制器。
在确定出该目标反馈控制器后，可根据该目标反馈控制器及所述第一空间状态方程的系统矩阵a′与控制矩阵b′，构建飞行器有壁面效应时的第一闭环系统。
具体地，有壁面效应时的开环系统的表达式如下：
g′(s)＝c(si-a′)-1b′+d；
式中各字母表达的含义请参阅上文。
有壁面效应时的闭环系统(即所述第一闭环系统)的表达式如下：
该式中，k的取值即为所述目标反馈控制器的控制器矩阵。
步骤205、确定能使所述第一闭环系统维持稳定的所述距离的最小值，得到飞行器至壁面的最小安全距离。
在有壁面效应时，由于dwe/r变化，系统合外力向量fb和气动力矩向量mb与倾转力矩矢量等均发生了变化，导致涵道式无人机的动力学模型表达式也发生了变化，相应也会导致闭环系统
步骤206、基于所述最小安全距离，对飞行器进行飞行控制。
最终，可基于所述最小安全距离，在飞行器需抵近壁面悬停以执行空中作业时对飞行器进行飞行控制。
其中，在飞行器抵近壁面工作时，控制飞行器与壁面之间的距离至少不小于该最小安全距离，以此保障飞行器在空中抵近壁面作业时的稳定性及安全性。具体地，可在大于等于该最小安全距离的范围内，根据飞行器的构型和/或控制器的类型来设定飞行器抵近壁面悬停时飞行器与壁面之间的最小允许抵近距离，该最小允许抵近距离处于大于等于所述最小安全距离的范围内，以此来确保飞行器在抵近壁面悬停工况下进行作业时的安全性与稳定性。
需要说明的是，同一类型、型号的无人机在选定效果良好的反馈控制器后，其最小安全距离不变，从而确定无人机至壁面的最小安全距离的处理过程可以预先完成，后续，可直接基于该预先确定出的最小安全距离对无人机进行抵近壁面作业时的飞行控制。
综上，相比于开放旋翼式飞行器，涵道式飞行器可以满足高空抵近飞行的需求，且相比于现有方案，本申请研究了飞行器抵近壁面时所产生的壁面效应与飞行器距离壁面间距的关系，并将其所带来的影响纳入到飞行器模型的构建中一起考虑，通过分析得到飞行器至壁面的距离和系统稳定性的关系，进而转化得到一个允许抵近的最小安全距离，也即整机系统稳定前提下飞行器与壁面的最小安全距离，而基于该考虑了壁面效应所得的最小安全距离对飞行器进行飞行控制，显然可使得飞行器抵近壁面飞行(主要是指抵近壁面悬停以执行作业的工况)时的稳定性及安全性得以提升。
对应于上述的飞行器的飞行控制方法，本申请可选实施例还公开了一种飞行器的飞行控制装置，参阅图7，该飞行控制装置包括：
第一确定单元701，用于确定壁面效应下飞行器的合力矢量及合力矩矢量与飞行器至壁面的距离之间的关联关系；
第一构建单元702，用于基于所述关联关系构建飞行器有壁面效应时的第一动力学模型；所述第一动力学模型中包括基于所述距离表达的所述合力矢量及所述合力矩矢量；
第二确定单元703，用于基于所述第一动力学模型确定飞行器有壁面效应时的第一空间状态方程；所述第一空间状态方程的系统矩阵与控制矩阵中包括所述距离；
第二构建单元704，用于利用一给定的目标反馈控制器及所述第一空间状态方程的系统矩阵与控制矩阵，构建飞行器有壁面效应时的第一闭环系统；所述目标反馈控制器为能使飞行器无壁面效应时的第二闭环系统维持稳定的反馈控制器；
第三确定单元705，用于确定能使所述第一闭环系统维持稳定的所述距离的最小值，得到飞行器至壁面的最小安全距离；
控制单元706，用于基于所述最小安全距离，控制飞行器的飞行。
在本申请实施例的一可选实施方式中，飞行器至壁面的距离为飞行器旋翼中心到壁面的距离dwe，所述合力矢量包括：飞行器在有壁面效应悬停工况时的系统总升力矢量与重力矢量；所述合力矩矢量包括：飞行器在有壁面效应悬停工况时的反扭矩矢量与倾转力矩矢量；
所述第一确定单元701，具体用于：
确定飞行器的系统总升力矢量与距离比dwe/r之间的关联关系；
确定飞行器的反扭矩矢量与距离比dwe/r之间的关联关系；
确定飞行器的倾转力矩矢量与距离比dwe/r之间的关联关系；
基于系统总升力矢量、反扭矩矢量、倾转力矩矢量分别与距离比dwe/r之间的关联关系，确定系统总升力矢量、反扭矩矢量、倾转力矩矢量分别与距离dwe之间的关联关系；
其中，所述距离比dwe/r为飞行器旋翼中心到壁面的距离dwe与飞行器螺旋桨半径r的比值。
在本申请实施例的一可选实施方式中，如图8所示，还可以包括：第三构建单元707，用于：
在所述第一构建单元702基于所述关联关系构建飞行器有壁面效应时的第一动力学模型之前，构建飞行器无壁面效应时的第二动力学模型；所述第二动力学模型的输入包括除去重力外飞行器所受到的合外力向量fb、飞行器整体所受到的气动力矩向量mb及飞行器重力fg，输出包括飞行器机体的线速度向量、角速度向量及欧拉角向量，飞行器的系统总升力矢量为所述合外力向量fb在机体z轴方向上的分力，飞行器的反扭矩矢量为所述气动力矩向量mb绕所述z轴的力矩量。
在本申请实施例的一可选实施方式中，所述第一构建单元702，具体用于：
基于所述关联关系确定对所述系统总升力矢量进行修正的修正因子α与对所述反扭矩矢量进行修正的修正因子β，并确定所述倾转力矩矢量的表达式；所述修正因子α、β及所述倾转力矩矢量的表达式中包括所述距离dwe；
利用所述修正因子α对所述第二动力学模型中的合外力向量fb在机体z轴方向上的分力进行修正；利用所述修正因子β对所述第二动力学模型中的气动力矩向量mb绕所述z轴的力矩量进行修正；并向所述第二动力学模型的输入中引入所述倾转力矩，得到飞行器有壁面效应时的第一动力学模型。
在本申请实施例的一可选实施方式中，所述第一动力学模型与所述第二动力学模型分别为一非线性系统；
所述第二确定单元703，具体用于：
在所述第一动力学模型的系统平衡点处，将所述第一动力学模型线性化为一线性系统；
基于预定辨识技术，确定所述第一动力学模型线性化后的线性系统对应的状态空间方程，得到飞行器有壁面效应时的第一状态空间方程；
所述第二构建单元704，具体用于：
在所述第二动力学模型的系统平衡点处，将所述第二动力学模型线性化为一线性系统；
基于预定辨识技术，确定所述第二动力学模型线性化后的线性系统对应的状态空间方程，得到飞行器无壁面效应时的第二状态空间方程；
基于所述第二状态空间方程，确定无壁面效应时飞行器的第二闭环系统；
确定能使飞行器无壁面效应时的所述第二闭环系统维持稳定的目标反馈控制器；
利用所述目标反馈控制器及所述第一空间状态方程的系统矩阵与控制矩阵，构建飞行器有壁面效应时的第一闭环系统。
对于本申请实施例公开的飞行器的飞行控制装置而言，由于其与上文实施例中公开的飞行器的飞行控制方法相对应，所以描述的比较简单，相关相似之处请参见上文实施例中飞行器的飞行控制方法部分的说明即可，此处不再详述。
另外，本申请还公开了一种飞行器，该飞行器为涵道式飞行器，更具体地，该飞行器可以是但不限于共轴反桨的双涵道无人机。参阅图8示出的飞行器的结构示意图，该飞行器可以包括：
机身801及至少两个涵道螺旋桨系统802；
其中，在所述飞行器包括两个涵道螺旋桨系统802的情况下，所述飞行器还可以包括两个控制舵，两个涵道螺旋桨系统802采用纵列形式，且对称设置于机身801两侧，两个控制舵分别固定连接在每个涵道螺旋桨系统802的涵道下方。在所述飞行器包括两个以上的涵道螺旋桨系统802的情况下，可以通过不同涵道中螺旋桨的差速转向实现飞行，当然，也可以借助控制舵实现飞行，借助控制舵可以使得控制更加稳定，效果更好。
该涵道式飞行器的具体组成结构及各组成部分的功能，可参阅图1以及上文中针对图1对涵道式无人机的结构及功能的相关介绍，这里不再赘述。
除此之外，所述飞行器还包括控制器804，用于基于如上文所述的飞行控制方法中确定的最小安全距离对飞行器进行飞行控制；或者，接收外部控制信号，并基于该控制信号对飞行器进行飞行控制，该控制信号为基于如上文所述的飞行控制方法中的最小安全距离所生成的信号。
具体地，作为一种可选实施方式，无人机等飞行器，可基于如上文所述的飞行控制方法中确定的最小安全距离，由自身控制器作为执行主体对飞行器进行飞行控制，以保障飞行器在空中抵近壁面飞行时的稳定性及安全性能；或者，作为另一种可选实施方式，还可以接收外部控制信号，该外部控制信号示例性地比如可以是无人机控制手柄或控制站基于所述最小安全距离生成的控制信号，无人机在接收到该外部控制信号后，则基于该外部控制信号对无人机抵近壁面工作的工况进行控制，通过控制飞行器与壁面之间的距离至少不小于所述最小安全距离，使得飞行器在空中抵近壁面飞行时的稳定性及安全性能得以保障。
综上所述，相比于开放旋翼式飞行器，涵道式飞行器可以满足高空抵近飞行的需求，且相比于现有方案，本申请研究了飞行器抵近壁面时所产生的壁面效应与飞行器距离壁面间距的关系，并将其所带来的影响纳入到飞行器模型的构建中一起考虑，通过分析得到飞行器至壁面的距离和系统稳定性的关系，转化得到一个允许抵近的最小安全距离，也即整机系统稳定前提下飞行器与壁面的最小安全距离，而基于该考虑了避免效应所得的最小安全距离对飞行器进行飞行控制，显然可使得飞行器工作时的稳定性及安全性得以提升。基于本申请方案，在无人机抵近壁面工作时，通过控制无人机与壁面之间的距离至少不小于所述最小安全距离，可使得飞行器在空中抵近壁面作业时的稳定性及安全性得以保障。
需要说明的是，本说明书中的各个实施例均采用递进的方式描述，每个实施例重点说明的都是与其他实施例的不同之处，各个实施例之间相同相似的部分互相参见即可。
为了描述的方便，描述以上系统或装置时以功能分为各种模块或单元分别描述。当然，在实施本申请时可以把各单元的功能在同一个或多个软件和/或硬件中实现。
通过以上的实施方式的描述可知，本领域的技术人员可以清楚地了解到本申请可借助软件加必需的通用硬件平台的方式来实现。基于这样的理解，本申请的技术方案本质上或者说对现有技术做出贡献的部分可以以软件产品的形式体现出来，该计算机软件产品可以存储在存储介质中，如rom/ram、磁碟、光盘等，包括若干指令用以使得一台计算机设备(可以是个人计算机，服务器，或者网络设备等)执行本申请各个实施例或者实施例的某些部分所述的方法。
最后，还需要说明的是，在本文中，诸如第一、第二、第三和第四等之类的关系术语仅仅用来将一个实体或者操作与另一个实体或操作区分开来，而不一定要求或者暗示这些实体或操作之间存在任何这种实际的关系或者顺序。而且，术语“包括”、“包含”或者其任何其他变体意在涵盖非排他性的包含，从而使得包括一系列要素的过程、方法、物品或者设备不仅包括那些要素，而且还包括没有明确列出的其他要素，或者是还包括为这种过程、方法、物品或者设备所固有的要素。在没有更多限制的情况下，由语句“包括一个……”限定的要素，并不排除在包括所述要素的过程、方法、物品或者设备中还存在另外的相同要素。
以上所述仅是本申请的优选实施方式，应当指出，对于本技术领域的普通技术人员来说，在不脱离本申请原理的前提下，还可以做出若干改进和润饰，这些改进和润饰也应视为本申请的保护范围。
- 还没有人留言评论。精彩留言会获得点赞！