一种大展弦比机翼后缘舵面展向间隙确定方法与流程

本发明属于飞行器结构设计技术领域，具体涉及一种大展弦比机翼后缘舵面展向间隙确定方法。

背景技术：

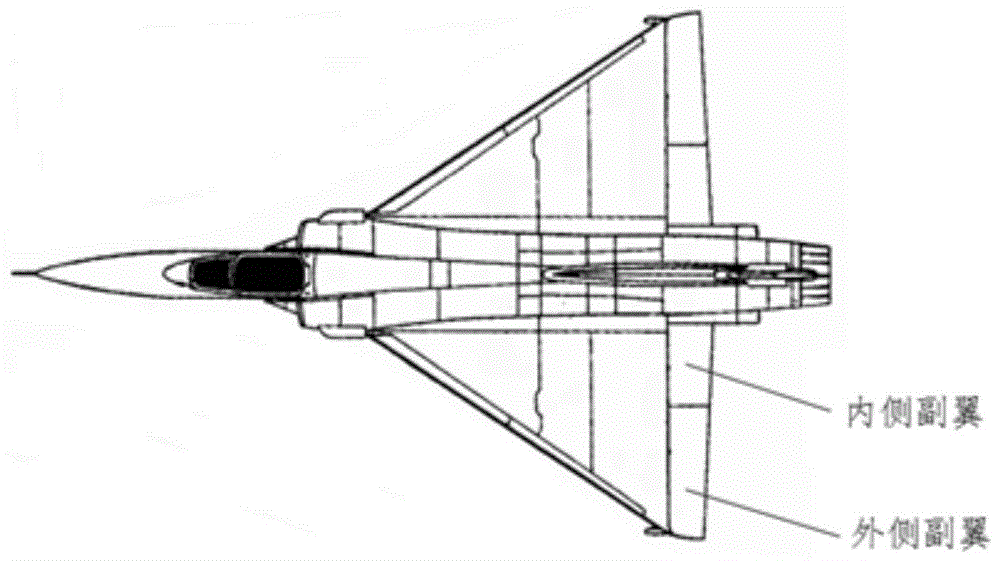
舵面位于机翼后缘，是飞机的重要控制舵面，可以提高飞机的机动性，改善飞机的起飞、着陆性能。战斗机的机翼后缘一般布置有2块舵面，即内侧舵面和外侧舵面，每一块舵面都通过铰链与主翼面连接，舵面安装位置见图1。为了避免运动碰撞干涉，内侧舵面和外侧舵面之间都会留一定的缝隙，见图2。这个缝隙一般是根据统计数据和经验确定，一般选5mm，并给一定的公差，如5(-1，2)等。

但是这种根据统计数据和经验确定舵面缝隙的方法没有充分考虑不同飞行器机翼在受载情况下的变形影响，在实际使用中，内侧舵面和外侧有时候会发生碰撞干涉的情况。比如某机型内侧舵面和外侧舵面后缘在高载大偏角的工况下发生碰撞干涉，干涉范围从后缘向前缘方向大约30mm，如图3和图4所示。

技术实现要素：

鉴于现有技术的上述问题，本发明的目的是提出一种大展弦比机翼后缘舵面展向间隙确定方法，以考虑机翼在高载以及舵面大偏角工况下的内侧舵面和外侧舵面之间间隙，从而较好地克服和避免舵面后缘碰撞干涉问题。

本发明的上述目的是利用以下技术方案实现的：

一种大展弦比机翼后缘舵面展向间隙确定方法，采用矩阵变换的方法计算出受载变形前后舵面端面的位置变化，从而求出最小需要舵面展向间隙。

所述的一种大展弦比机翼后缘舵面展向间隙确定方法，包括以下步骤：

获得主翼面变形引起的舵面转轴的偏移，根据舵面转轴的偏移，得到外侧舵面相对于内侧舵面的相对偏角；

然后根据坐标变换计算舵面上任意一点在沿偏移后的转轴偏转最大角度状态下的位置，并求出该位置在坐标变换前的初始位置，该位置与初始位置的差值就是理论舵面展向最小间隙。

其中，获得主翼面变形引起的舵面转轴的偏移，根据舵面转轴的偏移，得到外侧舵面相对于内侧舵面的相对偏角包括通过有限元分析或试验等手段，取得舵面每个交点的位移量，根据舵面转轴的偏移，得到外侧舵面相对于内侧舵面的相对偏角。

其中，坐标变换前的原坐标系的原点为外侧舵面转轴与外侧舵面端面的交点，这样，可以极大地减少计算量。

其中，所述原坐标系为右手坐标系oxyz，x轴正向沿转轴指向翼尖方向，y轴正方向指向后缘，z轴竖直向上为正方向，这样便于计算。

其中，所述方法还包括考虑制造公差、变形和振动，在理论舵面展向最小间隙的基础上适当增加间隙。

另外，实际计算中可以在边界位置选择有限的点位进行计算，以减少计算量。

本发明的方法可考虑机翼在高载以及舵面大偏角工况下的内侧舵面和外侧舵面之间间隙，从而较好地克服和避免舵面后缘碰撞干涉问题。

附图说明

图1为舵面安装位置示意图；

图2为內侧舵面(內副)和外侧舵面(外副)间的运动间隙的示意图；

图3为干涉部位的示意图；

图4为本发明方法的实施例中的计算点位置的示意图；

图5为舵面转轴变化情况的示意图。

具体实施方式

下面参考附图，结合具体实施例对本发明做进一步详细描述。

在高载大偏角工况下，舵面会发生偏移，内副和外副的转轴的相对位置也会发生变化，进而舵面沿转轴的偏转轨迹发生变化。因此分析时首先计算外侧舵面相对于内侧舵面的相对偏移量，然后再分析外侧舵面偏转后的相对位移量就可以确定舵面的间隙。

实际计算中，可以选取转轴与外副端面的交点作为坐标原点建立右手坐标系oxyz，x轴正向沿转轴指向翼尖方向，y轴正方向指向后缘，z轴竖直向上为正方向，如图4所示。

首先计算主翼面变形引起的舵面转轴的偏移。在高载工况下外侧舵面转轴的偏移量要大于内侧舵面转轴的偏移量。在实际设计中，可以通过有限元分析和试验等手段，取得舵面每个交点的位移量，从而可以计算出外侧舵面相对于内侧舵面的相对偏角θ。

根据前文的分析，在使用中外侧舵面的转轴会相对于内侧舵面转轴偏转一定角度θ，在这里相当于将xoz平面绕y轴旋转θ角。旋转可得到新的坐标系o′x′y′z′，其中y′轴与原坐标系的y轴重合，对应旋转矩阵aθ为

然后根据坐标变换计算舵面上任意一点在沿偏移后的转轴偏转最大角度状态下的位置，并求出该位置在坐标变换前的初始位置，该位置与初始位置的差值就是理论舵面展向最小间隙。

具体地，设舵面在使用中要沿转轴偏转最大角度δ。这个偏角应该在新的坐标系o′x′y′z′的基础上偏转，其变换矩阵为：

完成偏转变换求得偏转后位置以后，还要求出该位置在原坐标系中的位置，即恢复到初始坐标系oxyz，需乘以aθ变换的逆变换矩阵：

设选取的计算点在初始坐标系0xyz的坐标为(x0，y0，z0)，偏转之后的坐标为(xp，yp，zp)。则可得到

[xp，yp，zp，1]＝[x0，y0，z0，1]aθaδa′θ(1)

将式(1)展开后得到

xp＝x0cos²θ+y0sinθsinδ+

z0sinθ(cosδ-cosθ)(2)

yp＝y0cosδ-x0sinθsinδ(3)

zp＝-x0sinθcosθ+y0sinθcosθ+

z0(sin²θ+cosθcosδ)(4)

通过上述的方法可以计算出外侧舵面在最大偏角的偏移量，据此就可以初步确定内副和外副的间隙。

实际计算中可以在边界位置选择有限的点位进行计算，以减少计算量。

具体实例

某型飞机在机翼后缘设置有内侧舵面和外侧舵面，内副和外副的转轴平行、端面平行。内副和外副的运动工况均为在±30°的范围偏转，如图2所示。如果按经验内副和外副的缝隙设为5mm。但因为此飞机为高机动的战斗机，飞行工况复杂，载荷较大，因此需要考虑大过载工况舵面的正常使用。

1)主翼面变形引起的舵面偏移

有限元分析表明本型号飞机的机翼在最严重工况下翼尖最大位移达到200mm，而对应的内侧舵面和外侧舵面悬挂接头的位移情况见图5和表1，位移量均为垂直弦平面，位移量值为正表示向上，位移量为负表示向下。

表1舵面接头位移量

从表1可以看出，外副的位移量远大于內副，外副的3个接头相对于內副3号接头的相对位移量为：11.2mm、42.8mm和75.9mm，也就是说外侧舵面轴线相对于内侧舵面的轴线发生了偏转。计算可得外副轴线相对于内副轴线偏转角度为1.08°。

2)最大偏角状态下舵面偏移量的计算

计算中拟取外副上翼面和外副端面转折的棱边作为分析对象，从转轴部位到后缘均匀选取10个点作为分析对象，见图4。然后通过坐标变换来计算位移量。

选取转轴与外副端面的交点作为坐标原点建立右手坐标系oxyz，x轴正向沿转轴指向翼尖方向，y轴正方向指向后缘，z轴竖直向上为正方向，如图4所示。

根据已知条件和前文分析θ＝-1.08°，δ＝30°。

根据式(1)-(4)计算可得这10个点偏移过后在原坐标系的坐标值，其中xp与x0值的差即为对应点的偏移量，如果差值为负说明该点向內副方向移动，见表2。

表2外副端面典型位置偏移量

从表2可以看出，最大偏移量在a1点，也就是后缘的点，偏移量达到7.34mm。也就是说，在高载和最大偏角状态下，内副和外副的缝隙至少要达到7.34mm才能保证不碰撞。可见，如果采用统计规律按5mm给出舵面缝隙，不能保证舵面的正常使用。