一种环量控制翼型气动与电磁隐身联合优化方法

1.本发明涉及飞翼布局优化技术领域，具体是一种环量控制翼型气动与电磁隐身联合优化方法。


背景技术：

2.飞翼布局通常指没有尾翼且翼身融合，以整个翼身作为升力面的布局。采用飞翼布局的飞行器通常具有较高的升阻比和良好的电磁隐身性能，能够穿破对方防空系统，执行持久的监视和情报收集工作。
3.飞翼布局相比常规飞行器有着如下优势：其一，飞翼布局没有尾翼，翼身融合可以消除翼-尾涡流和激波的影响，减小飞行阻力；其二，整个机身作为升力面，翼面积较大因而翼载荷较低，即使是在空气稀薄的高空仍能提供足够升力，相比常规大展弦比高空长航飞行器减少了大翼展所需的结构重量；其三，取消尾翼的同时也取消掉了用于支撑尾翼的支撑结构，使得全机结构重量大大减轻，增大飞行器装载能力；最后，平滑的机身和取消尾翼消除了一些强散射源，使得全机的雷达反射面积显著减少，提高了飞行器的隐身性能。
4.飞翼布局飞行器的上述优势，使它受到世界范围内的广泛重视。但随着雷达预警探测系统的快速发展，飞翼布局使用传统舵面配平或机动时，仍将暴露于对方雷达之下，因而不能满足日益激烈的“探测与反探测”的生存需求。传统飞翼布局无人机的舵面偏转会破坏飞翼布局的平滑外形，同时，舵面偏转机构会在飞行器外表面上留下开孔和狭缝，形成电磁波反射源。为了消除舵面机构对飞行器隐身性能的影响，利用后缘环量控制设备替换舵面来进行无人机的飞行控制成为研究前沿。安装后缘环量控制设备的翼型被称为环量控制翼型(cca)，其部件名称和参数定义如图1所示。
5.图1中，坐标系原点o固定在翼型前缘点，翼型的弦向和法向分别为x轴和y轴方向。环量控制翼型的弦长为在x轴方向从翼型前缘点到射流出口位置的距离，定义为c。后缘射流机构包含coanda曲面、射流出口和高压气室。coanda曲面的半径定义为r。气体经过高压气室出口(射流出口)形成射流，射流夹带边界层流动让翼型产生气动型弯曲，进而改变翼型环量和升力，环量控制的原理如图2所示。在两侧机翼后缘分别使用环量控制设备，可以进一步产生姿态控制力矩。
6.使用环量控制设备代替传统舵面虽让飞机外表面减少了开孔和缝隙，同时避免了偏转舵面对雷达波的散射。但环量控制设备的安装将增大机翼后缘厚度，必然增强后向电磁散射强度。机翼上下表面和coanda曲面的几何形状决定了环量控制能力和翼型的电磁散射特性，因此有必要开展气动和隐身联合优化，同时提升翼型的气动和隐身特性。另一方面，环量控制翼型主要用于飞翼布局，其后掠角较大，机翼表面的展向流动显著。常规的二维翼型优化方法得到的优化翼型在三维飞翼布局上往往表现不佳。若直接开展三维飞翼布局整机优化，气动和隐身计算量又难以承受。


技术实现要素：

7.针对上述现有技术中的不足，本发明提供一种环量控制翼型气动与电磁隐身联合优化方法，提出了二维优化+三维验证的2.5d优化概念，在常规二维翼型优化基础上增加三维飞翼布局的验证流程，对优化结果继续优选，获得适用于三维飞翼布局的环量控制翼型。
8.为实现上述目的，本发明提供一种环量控制翼型气动与电磁隐身联合优化方法，包括如下步骤：
9.步骤1，获取翼型气动与电磁隐身联合优化的pareto前沿解；
10.步骤2，在pareto前沿解中选择气动性能占优、隐身性能占优以及气动隐身性能均衡的三个二维翼型；
11.步骤3，将选择的二维翼型作为飞翼布局飞行器外翼段的翼型1和翼型2，并放样生成翼型1和翼型2之间的外翼段，形成三种三维飞翼布局构型；
12.步骤4，对各三维飞翼布局构型进行三维的气动与隐身仿真分析，并根据三维飞翼布局构型的气动和隐身特性数据确定最终翼型选取。
13.在其中一个实施例，步骤1的过程具体为：
14.步骤1.1，绘制初始cca翼型网格，并在翼型上下表面以及coanda曲面上设置若干控制点，进行翼型参数化建模；
15.步骤1.2，基于ffd的翼型几何和网格变形，在设计空间内选取若干样本点，并收集每个样本点的气动数据与隐身数据，构建翼型气动与电磁隐身联合优化的代理模型；
16.步骤1.3，基于代理模型，以最小化前、后向
±
20
°
rcs均值、最大化升阻比为优化目标，以设计空间与俯仰力矩系数绝对值小于预设值为约束条件，经过遗传算法优化，得到翼型气动与电磁隐身联合优化的pareto前沿解。
17.在其中一个实施例，步骤1.1中，在翼型上下表面设置控制点的过程为：
18.在翼型上表面，沿弦向间隔设置若干第一控制点，其中，第一控制点在翼型前缘的分布密度大于在翼型后缘的分布密度；
19.在翼型下表面，沿弦向间隔设置若干第二控制点，其中，第二控制点在翼型前缘的分布密度大于在翼型后缘的分布密度。
20.在其中一个实施例，所述第一控制点的数量与所述第二控制点的数量相同且一一对应，相互对应的第一控制点与第二控制点位于翼型的同一法向上。
21.在其中一个实施例，所述第一控制点、所述第二控制点沿弦向分布位置为：
[0022][0023]
式中，x表示第n个第一控制点或第n个第二控制点到翼型前缘的距离，c为弦长，a、b为计算系数，n为第一控制点或第二控制点的数量，n＝1,2,
…
,n。
[0024]
在其中一个实施例，步骤1.1中，在coanda曲面上设置控制点的过程为：
[0025]
在半圆形coanda曲面上，设置若干沿周向均匀分布的第三控制点。
[0026]
在其中一个实施例，步骤1.2与步骤1.3中，所述设计空间为：
[0027]
对于翼型上下表面的控制点，其沿翼型法向的纵坐标变化范围为原始翼型厚度的20％；
[0028]
对于coanda曲面上的控制点，其沿coanda曲面径向移动范围为20％r，其中，r为
coanda曲面的半径。
[0029]
在其中一个实施例，步骤1.3中，所述俯仰力矩系数绝对值小于预设值，具体为：
[0030]
俯仰力矩系数绝对值小于或等于0.01。
[0031]
本发明提供的一种环量控制翼型气动与电磁隐身联合优化方法，具有如下有益技术效果：
[0032]
1、基于ffd方法的翼型表面和coanda曲面联合参数化建模：
[0033]
对于翼型上下表面，ffd方法的控制点在翼型前缘分布较密，可更准确地控制小曲率翼型前缘的几何变形；对于半圆形coanda曲面，控制点沿周向均匀分布，可更全面地控制整个coanda曲面的几何变形；这样的联合参数化建模方式产生的优化设计空间范围更大，分布更加合理。
[0034]
2、建立二维优化+三维验证的翼型2.5d优化流程：
[0035]
常规翼型优化终止于二维优化结果，但包含后缘射流机构的翼型主要应用平台为飞翼布局飞行器，飞翼布局常常具有较大的后掠角，机翼展向流动带来显著的三维效应。常规二维翼型优化结果往往无法在飞翼布局飞行器上表现出最佳气动和电磁隐身性能。同时在飞行器上，射流与绕流的相互作用方式与二维翼型的情况差异较大，因此射流在增升或飞行控制方面的效果将与二维翼型优化结果不同。
[0036]
本发明提出二维优化+三维验证的翼型2.5d优化流程，在常规二维翼型气动与电磁隐身多目标优化的基础上，增加在三维飞行器上的验证环节。在pareto前沿上选择气动性能占优、隐身性能占优和气动隐身性能均衡的三个二维翼型，替换飞翼布局飞行器外翼段原始翼型，形成三种构型，进行三维的气动与隐身模拟。根据三种构型的气动与隐身性能数据开展对比优选工作，从而获得面向特定飞翼布局飞行器的翼型优化结果。整个优化流程结合了传统二维翼型优化流程与新的三维飞行器平台验证流程，因此可视为一种2.5d优化流程，能够保证翼型在飞行器上能够展示出气动和电磁隐身特性优势。
附图说明
[0037]
为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图示出的结构获得其他的附图。
[0038]
图1为背景技术中环量控制翼型部件和参数定义的示意图；
[0039]
图2为背景技术中环量控制的原理图；
[0040]
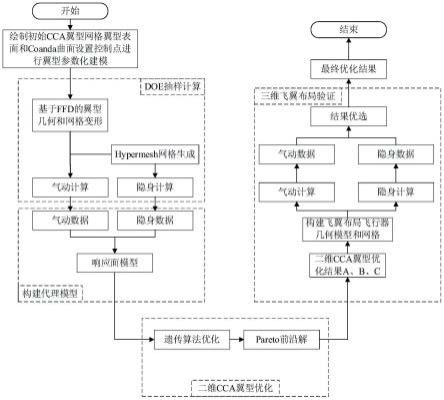
图3为本发明实施例中翼型气动与电磁隐身联合优化的流程图；
[0041]
图4为本发明实施例中初始cca翼型网格示意图；
[0042]
图5为本发明实施例中翼型变形控制点分布示意图；
[0043]
图6为本发明实施例中翼型几何变形范围示意图；
[0044]
图7为本发明实施例中cca翼型几何和网格变形示意图，其中，(a)为变形前的示意图，(b)为变形后的示意图；
[0045]
图8为本发明实施例中遗传算法优化解分布与pareto前沿解的示意图；
[0046]
图9为本发明实施例中优化翼型替换飞翼布局外翼段的示意图，其中，(a)为替换
前的示意图，(b)为替换后的示意图。
[0047]
本发明目的的实现、功能特点及优点将结合实施例，参照附图做进一步说明。
具体实施方式
[0048]
下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明的一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。
[0049]
需要说明，本发明实施例中所有方向性指示(诸如上、下、左、右、前、后
……
)仅用于解释在某一特定姿态(如附图所示)下各部件之间的相对位置关系、运动情况等，如果该特定姿态发生改变时，则该方向性指示也相应地随之改变。
[0050]
另外，在本发明中如涉及“第一”、“第二”等的描述仅用于描述目的，而不能理解为指示或暗示其相对重要性或者隐含指明所指示的技术特征的数量。由此，限定有“第一”、“第二”的特征可以明示或者隐含地包括至少一个该特征。在本发明的描述中，“多个”的含义是至少两个，例如两个，三个等，除非另有明确具体的限定。
[0051]
另外，本发明各个实施例之间的技术方案可以相互结合，但是必须是以本领域普通技术人员能够实现为基础，当技术方案的结合出现相互矛盾或无法实现时应当认为这种技术方案的结合不存在，也不在本发明要求的保护范围之内。
[0052]
如图3所示为本实施例公开的一种环量控制翼型气动与电磁隐身联合优化方法，其主要包括如下步骤1-4。
[0053]
步骤1，获取翼型气动与电磁隐身联合优化的pareto前沿解，其具体实施过程为：
[0054]
步骤1.1，利用网格绘制软件pointwise生成图4所示的初始cca翼型网格，然后在几何和网格变形软件sculptor中，在翼型上下表面以及coanda曲面上设置若干控制点，进行翼型参数化建模。
[0055]
本实施例中，在翼型上下表面以及coanda曲面上设置若干控制点的过程为：
[0056]
在翼型上表面，沿弦向间隔设置若干第一控制点，其中，第一控制点在翼型前缘的分布密度大于在翼型后缘的分布密度，即图5中的u1～u9；在翼型下表面，沿弦向间隔设置若干第二控制点，其中，第二控制点在翼型前缘的分布密度大于在翼型后缘的分布密度，即图5中的d1～d9；在半圆形coanda曲面上，设置若干沿周向均匀分布的第三控制点，即图5中的r
u1
～r
u4
、r0、r
d1
～r
d4
。其中，控制点(u1～u9,r1～d9,r
u1
～r
u4
,r0,r
d1
～r
d4
)即作为优化设计变量，共27个。第一控制点与第二控制点在翼型前缘分布较密，可更准确地控制小曲率前缘的几何变形。第三控制点沿coanda曲面周向均匀分布可更全面地控制整个coanda曲面的几何变形。该联合参数化建模方式产生的优化设计空间范围更大，分布更加合理。
[0057]
需要注意的是，虽然本实施例中图示的第一控制点、第二控制点、第三控制点的数量均为9个，但在实际应用过程中根据需要自适应的调整各控制点的数量。
[0058]
本实施例中，第一控制点与第二控制点一一对应，且相互对应的第一控制点与第二控制点位于翼型的同一法向上。例如，第一控制点、第二控制点沿弦向分布位置为：
[0059]
[0060]
式中，x表示第n个第一控制点或第n个第二控制点到翼型前缘的距离，c为弦长，a＝1.0392、b＝0.0372为计算系数，n为第一控制点或第二控制点的数量，n＝1,2,
…
,n。通过该公式可以将有限的控制点(控制点多了，求解空间的维度就大，不容易找到最优解，陷入“维度灾难”。)多分给前缘，后缘少分配控制点，进而有效地减少优化问题的求解维度。
[0061]
步骤1.2，基于ffd的翼型几何和网格变形，采用实验设计法(doe)在设计空间内选取若干样本点，并收集每个样本点的气动数据与隐身数据，构建翼型气动与电磁隐身联合优化的代理模型。
[0062]
参考图6，本实施例中的设计空间具体为：对于翼型上下表面的控制点，其沿翼型法向的纵坐标变化范围为原始翼型厚度的20％，翼型表面几何变化范围(即翼型表面的设计空间)被最大厚度和最小厚度翼型表面包络；对于coanda曲面上的控制点，coanda表面控制点r0沿coanda曲面径向移动范围为20％r,其它控制点按照比例变化，令coanda曲面几何变化范围(即coanda曲面的设计空间)被最大椭圆coanda曲面和最小椭圆coanda曲面包络。
[0063]
参考图7，对于所选取的每个样本点，可以通过在初始cca翼型网格的基础上移动控制点得到，依靠自由曲面变形技术(ffd)实现翼型几何和网格整体变形，从而实现对cca翼型的参数化表示。本实施例中代理模型的构建过程为：
[0064]
变形后的网格文件可直接用于气动计算，调用fluent开展气动计算，完成后可计算得到样本点对于翼型的升阻比k和俯仰力矩系数cm，即得到样本点的气动数据；
[0065]
变形后的cca翼型几何文件，使用hypermesh绘制网格用于隐身计算。使用feko可计算得到样本点对于翼型的前向、后向
±
20
°
rcs，即得到样本点的隐身数据；
[0066]
在isight中构建优化流程，收集每个样本点的气动和隐身数据，即可构建翼型气动与电磁隐身联合优化的代理模型。
[0067]
步骤1.3，基于代理模型，以最小化前、后向
±
20
°
rcs均值最大化升阻比k为优化目标，以设计空间与俯仰力矩系数cm的绝对值小于或等于0.01为约束条件，经过遗传算法优化，得到翼型气动与电磁隐身联合优化的pareto前沿解，即图8所示。
[0068]
需要注意的是，关于气动数据、隐身数据的计算过程，以及isight构建代理模型的过程与遗传算法的优化过程均为所属领域的常规技术手段，因此本实施例中不再对其进行赘述。
[0069]
步骤2，在pareto前沿解中选择气动性能占优、隐身性能占优以及气动隐身性能均衡的三个二维翼型，其中，气动性能占优指的是pareto前沿解中升阻比k最大的优化解，即图8找那个点c代表的翼型c；隐身性能占优指的是pareto前沿解中前、后向
±
20
°
rcs均值最小的优化解，即图8找那个点a代表的翼型a；气动隐身性能均衡指的是pareto前沿解中点c与电a连线中间区域的优化解，即图8找那个点b代表的翼型b。与对初始翼型相比，优化翼型a、优化翼型b、优化翼型c的优化结果如表1-2所示：
[0070]
表1优化翼型与初始翼型气动特性参数对比
[0071][0072]
表2优化翼型与初始翼型rcs均值对比
[0073][0074]
从表1-2可知，相对原始翼型，优化翼型a、优化翼型b、优化翼型c的升阻比有显著提升，rcs明显减小。
[0075]
步骤3，将选择的二维翼型作为飞翼布局飞行器外翼段的翼型1和翼型2(即将同一二维翼型分别作为翼型1和翼型2)，并放样生成翼型1和翼型2之间的外翼段，形成三种三维飞翼布局构型，即图9所示；
[0076]
步骤4，对各三维飞翼布局构型进行三维的气动与隐身仿真分析，并收集气动与隐身数据如表3-4所示：
[0077]
表3优化翼型与初始翼型应用于飞翼布局的气动数据
[0078][0079]
表4优化翼型与初始翼型应用于飞翼布局的隐身数据
[0080][0081][0082]
各三维飞翼布局构型的气动和隐身特性数据确定最终翼型选取。例如，根据表3-4
中三种优化翼型和初始翼型的飞翼布局气动和隐身特性数据可以发现，优化翼型a和优化翼型b布局的升阻比小于原始翼型布局。因此二维翼型优化结果应用到三维飞行器上并不一定能够展示出优越性。但优化翼型c布局的升阻比显著大于初始翼型布局，同时其各个方位的rcs均小于初始翼型。因此翼型c可被优选为最终翼型选取。需要注意的是，若是出现三种优化翼型都没有同时满足升阻比最大、rcs最小的情况，则可根据当前翼型设计的应用需求选择气动性能占优或隐身性能占优或气动隐身性能均衡的优化翼型作为最终翼型选取，也可以在pareto前沿中继续选取对应的二维翼型，拓展至三维翼型中后，分析气动与隐身性能，并作出取舍。
[0083]
以上所述仅为本发明的优选实施例，并非因此限制本发明的专利范围，凡是在本发明的发明构思下，利用本发明说明书及附图内容所作的等效结构变换，或直接/间接运用在其他相关的技术领域均包括在本发明的专利保护范围内。