一种空间摄动影响下的共面绕飞编队构型维持方法及系统

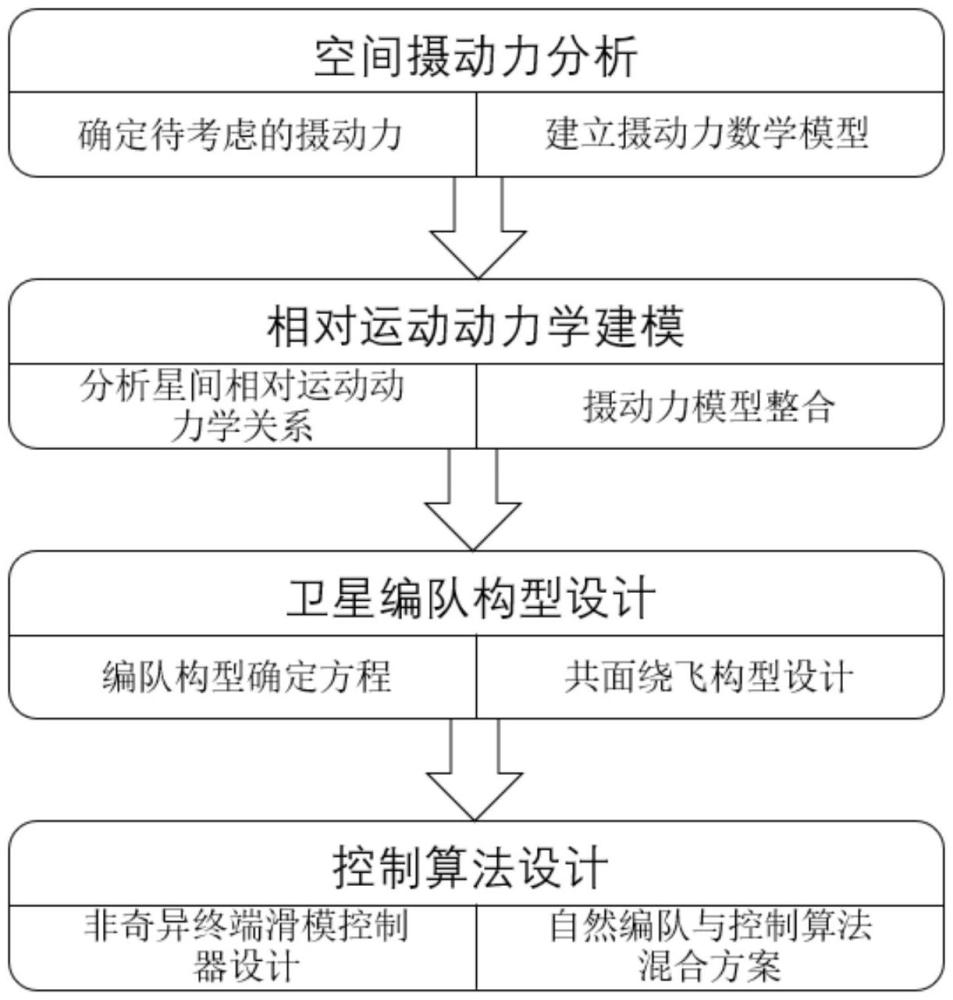
本发明涉及空间卫星编队与构型维持，具体为一种空间摄动影响下的共面绕飞编队构型维持方法及系统。

背景技术：

1、如今，空间任务需求日益复杂化、多样化，传统的单星系统难以在有限的载荷空间内实现更加强大的功能，星座系统也具有灵活性差、成本高、系统复杂等缺点。为了应对该问题，实现由多颗卫星通过精确测量与协同操作组成的飞行编队来代替传统方案变得更为重要。要实现任务需求并保持长期稳定的编队结构，需要克服许多挑战，卫星编队发射后需要进入并逐一调节轨道以形成编队结构。卫星编队飞行需要考虑卫星在空间中的相对运动和多普勒效应，此外，绕地卫星编队还要考虑卫星受轨道约束等。因此，卫星编队在控制、导航以及数据处理方面更加复杂。空间中长期在轨运行的卫星还会受到多种摄动力的影响：如非球形摄动、大气阻力摄动、太阳光压摄动、日月引力摄动等，即使是设计好的自然编队构型，其成员卫星也会因摄动力的存在而产生卫星轨道的漂移。为了圆满完成卫星地球观测、通信、导航等飞行任务，避免编队成员卫星之间的碰撞危险，需要对编队成员卫星的轨道进行维持，使轨道上每一点所对应的运动参数与上一周期的参数相比都尽量少地发生变化。传统的卫星编队构型维持方法往往需要求出卫星之间相对运动方程的解析解，并根据解析解求出环绕星的轨道根数以及运动方程，而加入摄动力的相对运动方程的解析解的求解过程十分复杂，需要对摄动项进行线性化处理，会使最终结果产生不可避免的偏差。因此，传统的卫星编队构型维持方法难以维持受到j2项摄动与大气阻力摄动影响下的共面绕飞编队卫星的构型。

技术实现思路

1、本发明的目的是：针对传统的卫星编队构型维持方法难以维持受到j2项摄动与大气阻力摄动影响下的共面绕飞编队卫星的构型的问题，提出一种空间摄动影响下的共面绕飞编队构型维持方法及系统。

2、本发明为了解决上述技术问题采取的技术方案是：

3、一种空间摄动影响下的共面绕飞编队构型维持方法，包括以下步骤：

4、步骤一：针对j2项摄动和大气阻力摄动，分别建立j2项摄动力数学模型和大气阻力摄动力数学模型；

5、步骤二：将j2项摄动力数学模型和大气阻力摄动力数学模型，带入cw方程，得到加入了摄动力的状态空间方程；

6、步骤三：利用轨道六根数方法设计共面绕飞的自然编队构型；

7、步骤四：基于共面绕飞的自然编队构型，并采用四阶龙格库塔法，得到二体运动条件下，每一时刻环绕卫星在lvlh坐标系下相对于主星的位置和速度；

8、步骤五：将每一时刻环绕卫星在lvlh坐标系下相对于主星的位置和速度作为当前坐标，并利用加入摄动力的相对运动动力学方程设计非奇异终端滑模控制器；

9、步骤六；利用非奇异终端滑模控制器完成共面绕飞编队构型维持。

10、进一步的，所述j2项摄动力数学模型表示为：

11、

12、归一化的球谐函数由下面递推公式具体求解：

13、

14、其中，j2项摄动力数学模型右侧第一项表示地球中心引力，后两项为地球非球形引力，re和μ分别为地球参考半径和地球引力常数，为卫星在国际地球参考系中的地心距、地心纬度和地心经度，n为所选重力场模型的阶数，m为所选重力场模型的次数，当m≠n时，cnm和snm将地球描述成凹凸相似的棋盘图案，称为地球非球形摄动的田谐项；当m＝n时，cnm和snm会把地球描述成凸和凹的扇形图案，称为地球非球形摄动的扇谐项；对cnm和snm进行归一化，则其中δ为中间变量，表示前一个迭代步n-1和前一个迭代步m-1下的状态；表示前一个迭代步n-1和当前条件m下的状态，表示前一个迭代步m-1和当前条件n下的状态，表示当前条件n和m下的状态；

15、所述大气阻力摄动力数学模型表示为：

16、

17、

18、

19、其中，cd为阻力系数，为面质比，ρ为大气密度，为卫星相对大气的速度，v和va分别为卫星和大气相对于地心的速度，x和y分别为卫星和大气相对于地心的速度，φ为卫星所在地的地心维度，ωe为地球的角速度矢量。

20、进一步的，所述步骤二的具体步骤为：

21、将j2项摄动力数学模型和大气阻力摄动力数学模型，整合到一般形式的cw方程中，作为研究的状态空间方程，cw方程的一般形式表示为：

22、

23、其中，ρ＝rc-rs＝[x y z]t为伴随航天器相对主航天器的位置坐标矢量，为伴随航天器相对主航天器的加速度坐标矢量，δfx、δfy、δfz为相对坐标系下伴随航天器相对于主航天器的除地球中心引力外所受到的所有摄动力和控制力带来的加速度的三轴分量，ε为平均轨道速率；

24、在一般的cw方程中加入摄动力，即将j2项摄动力数学模型和大气阻力摄动力数学模型写成加速度的表达形式带入到δfx、δfy、δfz三项中，考虑j2项摄动力数学模型和大气阻力摄动力数学模型，非球形摄动j2项产生的加速度形式如下：

25、j2(r)＝-(3/2)(j2μre2/r4)[(1-3sin2isin2θ)x

26、+(2sin2isinθcosθ)y+(2sinicosisinθ)z]

27、其中，r为卫星的位置矢量，j2为地球引力场势能的二次球谐项，x、y、z表示lvlh坐标系中的航天器坐标，re为地球平均赤道半径，i为轨道倾角，θ为升交角距，x、y、z为相应坐标系三轴的单位方向矢量；

28、将j2(r)带入cw方程的一般形式，并进行线性化后，得到改进的相对运动动力学方程，表示为：

29、

30、其中，rref为圆形参考轨道的恒定半径，iref为参考航天器的初始轨道倾角，t为给定时间，参数c，k，l，q用于校正j2效应引起的节点飘漂移的圆形参考轨道周期：

31、

32、φ0＝cos-1[cosiccosis+sinicsiniscosδω0]

33、

34、其中，s、γ0、φ0、δω0为中间变量，为δz0的一阶导数，δz0为初始状态下主航天器与伴随航天器在lvlh系下z轴方向坐标之差，is为主航天器的初始轨道倾角，由于主航天器最初是位于圆形参考轨道上，因此将is设置为iref；ic为参考航天器的初始轨道倾角；

35、在改进的相对运动动力学方程的基础上，代入大气阻力引起的加速度，表示为：

36、

37、其中，fdrag,x、fdrag,y、fdrag,z分别表示径向、轨道内和轨道法向上由于空气动力学阻力而产生的附加加速度；联立方程使用圆形参考轨道，则航天器相对于旋转大气的速度表达式如下：

38、

39、其中，分别为x,y,z的一阶导数，代入方程后得到如下加入了摄动力的状态空间方程：

40、

41、其中，表示在x轴方向进行计算，表示在y轴方向进行计算，表示在z轴方向进行计算。

42、进一步的，所述共面绕飞的自然编队构型的编队构型参数包括：绕飞椭圆短半径p，垂直轨道面方向的运动振幅s，初始相位差α，绕飞椭圆初始相位σ，绕飞椭圆中心沿航迹距离l；

43、p＝aea，s＝aδi，α＝σ-ψ，l＝aδλ，由如下表达式求得：

44、

45、环绕星偏心率映射表达式如下：

46、

47、其中，arctan为反正弦函数，ψ和δλ为中间变量；

48、针对圆形参考轨道，eref＝0，则有

49、环绕星轨道倾角映射表达式如下：

50、

51、环绕星升交点赤经映射表达式为ωcir＝ωref+δω；

52、环绕星近地点幅角映射表达式为

53、环绕星平近点角映射表达式为：

54、

55、其中，a为轨道半长轴，表示轨道的大小，ea表示两颗卫星相对升交点处的偏心率，ecir和eref分别为环绕星和主星的轨道偏心率，ωcir和ωref分别为环绕星和主星的近地点幅角，mcir和mref分别为环绕星和主星的平近点角，icir为环绕星的轨道倾角，ωcir和ωref分别为环绕星和主星的升交点赤经，ψ和δλ均为中间参数，δω为两卫星轨道的升交点赤经之差，δi为两卫星轨道之间的夹角，arccos为反余弦函数。

56、进一步的，所述步骤五的具体步骤为：

57、将状态空间方程写成的形式，表示为：

58、

59、其中ux,uy,uz为三轴的控制输入，t为仿真时间，将上式写成如下形式的二阶非线性动态系统：

60、

61、可得：

62、

63、针对卫星的相对位置误差以及相对速度误差进行跟踪，因此x＝[x1 x2]t由e＝[e1e2]t进行替代，且e1为位置误差，e2为速度误差，则滑模面表示为非奇异终端滑模控制器u设计为如下形式：

64、

65、其中，f(x)为状态空间方程中的无摄动项、g(x)表示摄动力干扰、b(x)为增益矩阵、β、e＝[e1 e2]t、lg和η均为滑模控制中的调节参数，β取1e-3，lg≥g(x)，且lg取2e-10，η取1e-11。

66、一种空间摄动影响下的共面绕飞编队构型维持系统，所述系统包括数学模型构建模块、状态空间方程构建模块、编队构型构建模块、二体运动模块以及滑模控制模块；

67、所述数学模型构建模块用于针对j2项摄动和大气阻力摄动，分别建立j2项摄动力数学模型和大气阻力摄动力数学模型；

68、所述状态空间方程构建模块用于将j2项摄动力数学模型和大气阻力摄动力数学模型，带入cw方程，得到加入了摄动力的状态空间方程；

69、所述编队构型构建模块用于利用轨道六根数方法设计共面绕飞的自然编队构型；

70、所述二体运动模块用于基于共面绕飞的自然编队构型，并采用四阶龙格库塔法，得到二体运动条件下，每一时刻环绕卫星在lvlh坐标系下相对于主星的位置和速度；

71、所述滑模控制模块用于将每一时刻环绕卫星在lvlh坐标系下相对于主星的位置和速度作为当前坐标，并利用加入摄动力的相对运动动力学方程设计非奇异终端滑模控制器，最后利用非奇异终端滑模控制器完成共面绕飞编队构型维持。

72、进一步的，所述j2项摄动力数学模型表示为：

73、

74、归一化的球谐函数由下面递推公式具体求解：

75、

76、其中，方程右侧第一项表示地球中心引力，后两项和为地球非球形引力，re和μ分别为地球参考半径和地球引力常数，为卫星在国际地球参考系中的地心距、地心纬度和地心经度，n为所选重力场模型的阶数，m为所选重力场模型的次数，当m≠n时，cnm和snm将地球描述成凹凸相似的棋盘图案，称为地球非球形摄动的田谐项；当m＝n时，cnm和snm会把地球描述成凸和凹的扇形图案，称为地球非球形摄动的扇谐项；对cnm和snm进行归一化，则其中δ为中间变量，表示前一个迭代步n-1和前一个迭代步m-1下的状态；表示前一个迭代步n-1和当前条件m下的状态，表示前一个迭代步m-1和当前条件n下的状态，表示当前条件n和m下的状态；

77、所述大气阻力摄动力数学模型表示为：

78、

79、

80、

81、其中，cd为阻力系数，为面质比，ρ为大气密度，为卫星相对大气的速度，v和va分别为卫星和大气相对于地心的速度，x和y分别为卫星和大气相对于地心的速度，φ为卫星所在地的地心维度，ωe为地球的角速度矢量。

82、进一步的，所述状态空间方程构建模块具体执行如下步骤：

83、将j2项摄动力数学模型和大气阻力摄动力数学模型，整合到一般形式的cw方程中，作为研究的状态空间方程，cw方程的一般形式表示为：

84、

85、其中，ρ＝rc-rs＝[x y z]t为伴随航天器相对主航天器的位置坐标矢量，为伴随航天器相对主航天器的加速度坐标矢量，δfx、δfy、δfz为相对坐标系下伴随航天器相对于主航天器的除地球中心引力外所受到的所有摄动力和控制力带来的加速度的三轴分量，ε为平均轨道速率；

86、在一般的cw方程中加入摄动力，即将j2项摄动力数学模型和大气阻力摄动力数学模型写成加速度的表达形式带入到δfx、δfy、δfz三项中，考虑j2项摄动力数学模型和大气阻力摄动力数学模型，非球形摄动j2项产生的加速度形式如下：

87、j2(r)＝-(3/2)(j2μre2/r4)[(1-3sin2isin2θ)x

88、+(2sin2isinθcosθ)y+(2sinicosisinθ)z]

89、其中，r为卫星的位置矢量，j2为地球引力场势能的二次球谐项，x、y、z表示lvlh坐标系中的航天器坐标，re为地球平均赤道半径，i为轨道倾角，θ为升交角距，x、y、z为相应坐标系三轴的单位方向矢量；

90、将j2(r)带入cw方程的一般形式，并进行线性化后，得到改进的相对运动动力学方程，表示为：

91、

92、其中，rref为圆形参考轨道的恒定半径，iref为参考航天器的初始轨道倾角，t为给定时间，参数c，k，l，q用于校正j2效应引起的节点飘漂移的圆形参考轨道周期：

93、

94、φ0＝cos-1[cosic cosis+sinic sinis cosδω0]

95、

96、其中，s、γ0、φ0、δω0为中间变量，为δz0的一阶导数，δz0为初始状态下主航天器与伴随航天器在lvlh系下z轴方向坐标之差，is为主航天器的初始轨道倾角，由于主航天器最初是位于圆形参考轨道上，因此将is设置为iref；ic为参考航天器的初始轨道倾角；

97、在改进的相对运动动力学方程的基础上，代入大气阻力引起的加速度，表示为：

98、

99、其中，fdrag,x、fdrag,y、fdrag,z分别表示径向、轨道内和轨道法向上由于空气动力学阻力而产生的附加加速度；联立方程使用圆形参考轨道，则航天器相对于旋转大气的速度表达式如下：

100、

101、其中，分别为x,y,z的一阶导数，代入方程后得到如下加入了摄动力的状态空间方程：

102、

103、其中，表示在x轴方向进行计算，表示在y轴方向进行计算，表示在z轴方向进行计算。

104、进一步的，所述共面绕飞的自然编队构型的编队构型参数包括：绕飞椭圆短半径p，垂直轨道面方向的运动振幅s，初始相位差α，绕飞椭圆初始相位σ，绕飞椭圆中心沿航迹距离l；

105、p＝aea，s＝aδi，α＝σ-ψ，l＝aδλ，由如下表达式求得：

106、

107、环绕星偏心率映射表达式如下：

108、

109、其中，arctan为反正弦函数，ψ和δλ为中间变量；针对圆形参考轨道，eref＝0，则有环绕星轨道倾角映射表达式如下：

110、

111、环绕星升交点赤经映射表达式为ωcir＝ωref+δω；

112、环绕星近地点幅角映射表达式为环绕星平近点角映射表达式为：

113、

114、其中，a为轨道半长轴，表示轨道的大小，ea表示两颗卫星相对升交点处的偏心率，ecir和eref分别为环绕星和主星的轨道偏心率，ωcir和ωref分别为环绕星和主星的近地点幅角，mcir和mref分别为环绕星和主星的平近点角，icir为环绕星的轨道倾角，ωcir和ωref分别为环绕星和主星的升交点赤经，ψ和δλ均为中间参数，δω为两卫星轨道的升交点赤经之差，δi为两卫星轨道之间的夹角，arccos为反余弦函数。

115、进一步的，所述滑模控制模块具体执行如下步骤：

116、将状态空间方程写成的形式，表示为：

117、

118、其中ux,uy,uz为三轴的控制输入，t为仿真时间，

119、将上式写成如下形式的二阶非线性动态系统：

120、

121、可得：

122、

123、针对卫星的相对位置误差以及相对速度误差进行跟踪，因此x＝[x1 x2]t由e＝[e1e2]t进行替代，且e1为位置误差，e2为速度误差，则滑模面表示为非奇异终端滑模控制器u设计为如下形式：

124、

125、其中，f(x)为状态空间方程中的无摄动项、g(x)表示摄动力干扰、b(x)为增益矩阵、β、e＝[e1 e2]t、lg和η均为滑模控制中的调节参数，β取1e-3，lg≥g(x)，且lg取2e-10，η取1e-11。

126、本发明的有益效果是：

127、本技术将摄动力在控制通道上进行直接补偿，并且非奇异终端滑模能够处理非线性的状态空间方程，因此不需要再次对加入摄动力的动力学方程进行线性化处理，避免了由于线性化造成的固有误差。因此，本技术技术方案可以有效的对受到j2项摄动与大气阻力摄动影响下的共面绕飞编队卫星的构型进行维持。