一种考虑司机室特性的起重机小车运行动态分析方法与流程

本发明属于动力学理论方法研究的技术领域，涉及一种考虑司机室特性的起重机小车运行动态分析方法。

背景技术：

起重机小车运行时会对主梁、司机室振动产生一定的影响，所以小车运行过程也是起重机设计与分析中需要关注的问题，小车-桥架耦合系统可简化为移动质量-梁耦合模型，从而进行动力学分析。一般情况下，在移动质量对简支梁动态特性影响的分析中，梁的挠度随着小车移动速度增大而增大，而且吊重摆动和移动质量的加速度对梁横向振动影响也不能忽略。司机室作为起重机司机的工作场所，其安装位置和安装方式都会对主梁动态特性产生影响。

技术实现要素：

本发明提供了一种考虑司机室特性的起重机小车运行动态分析方法，使起重机结构振动和司机烦恼率减小，提高了起重机的使用寿命，降低了司机振动产生职业病的概率。

为实现上述目的，本发明提供了一种考虑司机室特性的起重机小车运行动态分析方法，包括如下步骤：

1、根据起重机结构特征建立考虑司机室特性的物理振动模型，模型中司机室通过刚度和阻尼连接在主梁一端；

2、基于物理振动模型推导系统中动能、势能和耗散能的表达式；

3、通过拉格朗日法求解出与模型自由度相同数量的、独立的运行方程；

4、给定主梁振动响应初始值、和，吊重摆角初始值、、，以及司机室振动响应初始值、、均为零，通过主梁振动微分方程组计算在时刻主梁的动态响应、、；

5、将步骤4得到的结果代入吊重摆动微分方程和司机室振动的微分中，计算得到时刻吊重摆角响应、、以及司机室振动响应、、；

6、将步骤5得到的结果作为下一次迭代的初始值代入到步骤4中计算下一个时刻主梁振动响应，再重复步骤5操作，迭代计算步骤4和5，直到时间达到预先设定好的终止时间，最终得到了主梁、吊重摆角以及司机室振动的数值解；

7、判断计算结果、和的收敛性，如果不收敛则返回步骤（5）进行进一步的分析和计算。

所述步骤1考虑司机室特性的物理振动模型中包括：主梁垂直方向多自由度振动、吊重的摆动、司机室的垂直方向振动和小车垂直方向振动，其中主梁采用模态叠加法求解其振型。

所述步骤3中的运行方程包括：主梁振动微分方程、吊重摆动微分方程、司机室垂直方向振动的微分方程。

所述的主梁振动微分方程：

。

所述的吊重摆动微分方程：

。

所述的司机室垂直方向振动的微分方程：

。

附图说明

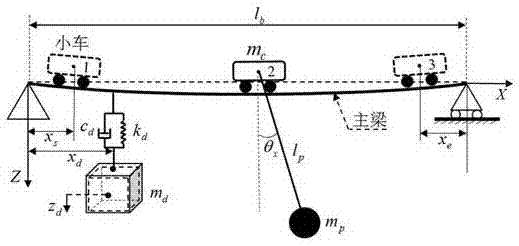
图1为本发明小车运行过程考虑司机室特性的物理振动模型

图2为本发明非线性振动方程计算流程图

图3为起重机小车运行的三种模式

图4小车运行速度对吊重摆角影响

图5钢丝绳长度对吊重摆角的影响

图6司机室连接刚度对主梁中心挠度影响

图7不同连接刚度下司机室位移响应

图8不同连接刚度下司机室和主梁间位移响应

图9不同连接刚度下司机室的振动加速度时域响应

图1中：为主梁杨氏模量；为主梁体密度；为主梁截面面积；为钢丝绳长度；为截面惯性矩；为小车质量；为吊重质量；为主梁单位长度质量；为钢丝绳长度；为司机室与主梁之间的连接刚度；为司机室与主梁之间的阻尼；为司机室质量；为司机室在安装位置坐标；为重力加速度；为小车最大运行速度；为主梁结构的第i阶振型阻尼比；为小车运行左侧极限位置；为小车运行右侧极限位置；为吊重摆动的摆角。

具体实施方式

以下结合附图，进一步说明本发明的具体实施过程。

如图1所示，建立本发明小车运行过程主梁振动物理模型，并基于此模型进行推导，

小车以最大速度在主梁上做变速运行，主梁上z方向处在时刻的弹性位移曲线可如下表示：

式中：为主梁弹性位移主梁广义坐标；为广义坐标数目。

简支梁的第i阶模态可表示为：

依据图1中所简化的物理模型可以定义各质量的坐标向量，在该坐标系下，主梁上各元素的位置向量、小车位置向量、吊重位置向量和起重机司机室位置向量可分别表示为：

假设系统的总动能为，其中两根主梁中的能量为，移动小车的运行动能为，吊重的动能为，系统中各部分的动能分别表示为：

在耦合系统模型中，系统势能包括：主梁的弹性应变能；主梁与司机室之间等效弹簧的弹性势能；在运动过程中，小车、司机室和吊重自身的重力所做的总功也会改变系统的势能。因此，起重机振动系统的总势能可表示为：

根据弹性力学理论，主梁的弹性应变所产生的弹性应变能为：

主梁和司机室之间的等效连接弹簧的弹性势能为：

起重机大车、小车和司机室在系统振动过程中自身重力所做的总功为：

将式（12）-（14）代入式（11）中，系统中的总势能可表示为：

系统中耗散能主要包括结构阻尼和司机室连接阻尼对系统能量的消耗，总耗散能可表示为：

在式(16)中的主梁结构阻尼可以通过式(17)和(18)求得。

等截面简支梁的第i阶圆频率为：

主梁第i阶振型的结构阻尼可表示为：

式中：第i阶振型的阻尼比。

非保守系统的拉格朗日方程可表示为：

式中：为系统的动能；为系统的势能；为系统的能量耗散函数；为因能量耗散函数而引起的阻尼力；仅代表外部作用的广义激振力；为广义坐标；为广义速度。

依据式(19)所示的非保守系统拉格朗日方程和系统能量的计算方法，可推导出系统运动微分方程，其中主梁的振动微分方程为：

吊重摆动的微分方程可表示为：

司机室振动的微分方程可表示为：

选取newmark法求解上述振动微分方程的数值解，newmark法提出了新的位移和速度的关系如式（4）和式（5）所示，

通过改变参数β和γ的取值，可以得到多种算法，如：β=0.25、γ=0.5为平均加速度法；β=0、γ=0.5为中心差分法等。当满足式（6）条件时newmark法可以实现无条件稳定。时刻系统振动方程的矩阵形式如式（7）所示，

因此，newmark法求解时刻响应是通过时刻的运动方程求得，为了求未知位移，可以将方程中的速度和加速度通过未知位移和其他常量表示，由公式（4）可得：

将上式代入式（5）中可得：

将式（8）和（9）代入（7）中可得：

式（10）中矩阵的计算方法参见式（11）和式（12）。

根据上述newmark法基本原理，系统振动求解步骤如下：

1、首先给定主梁振动响应初始值、和，吊重摆角初始值、、，以及司机室振动响应初始值、、均为零，通过主梁振动微分方程组计算在时刻主梁的动态响应、、；

2、将上述得到的结果代入吊重摆动微分方程和司机室振动的微分中，计算得到时刻吊重摆角响应、、以及司机室振动响应、、；

3、将上步得到的结果作为下一次迭代的初始值代入到步骤4中计算下一个时刻主梁振动响应，再重复步骤5操作，迭代计算步骤4和5，直到时间达到预先设定好的终止时间，最终得到了主梁、吊重摆角以及司机室振动的数值解；

4、判断计算结果、和的收敛性，如果不收敛则返回步骤（5）进行进一步的分析和计算。

上述完成了对系统模型的求解。

以下结合附图1-9和发明人依据发明的技术方案所完成的具体实施方案，从而对本发明作进一步的详细阐述，某起重机振动系统初始参数取值如表1所示，结果分析如下：

表1铸造起重机刚柔耦合系统参数取值。

(1)小车加速和减速的时间均设置为5s，小车运行轨迹是从一侧极限位置运行到另一侧极限位置，某起重机小车最大运行速度，以保证在小车运行过程中的安全性，小车三种运行模式如图3所示。

(2)如图4小车不同运行速度下吊重摆角响应，从图中可以看出：最大速度为运行模式下，0~5s时小车处于加速阶段吊重摆角呈现先增大后减小趋势；5~20s时小车处于匀速运动状态，吊重呈现往复周期性摆动，20~25s时小车处于减速阶段，吊重摆角先增大后减小。

(3)图5所示为钢丝绳长度对吊重摆角的影响。在0~5s加速阶段，不同绳长下吊重摆角幅值差别不大，5~60s匀速运行阶段，摆角幅值随摆线长度增大而增大，60~65s减速运行阶段，摆角振幅与摆线长度没有必然的线性关系。

(4)司机室连接刚度对主梁跨中振动的影响如图6所示，从图中可以看出，当连接刚度为时，跨中振动非线性波动明显，而当连接刚度为时，振动非线性波动不明显，振幅随着连接刚度增大而减小。

(5)在起重机工作过程中，司机室振动直接影响司机的工作舒适性，对司机室振动产生直接影响因素为司机室的连接刚度。图7—图9为不同刚度下司机室振动响应。从图7中可以看出，司机室连接刚度越大司机室振动振幅越小，当时司机室振动振幅基本为零，而当连接刚度时，司机室的振幅波动很大，非线性波动明显，最大振幅为7.7mm。

(6)从图8中可以看出，当连接刚度为时司机室与主梁相对位移基本为0，当时，司机室与主梁相对位移最大为5.2mm。

从图9中可以看出，司机室连接刚度为和时，司机室垂直向上的最大振动加速度分别为4.5m/s²、1.8m/s²、0.6m/s²和0.2m/s²，司机室连接刚度越大，司机室振动加速度越小。