一种基于九轴陀螺仪的电梯平台定位系统的制作方法

本发明属于定位技术领域，具体涉及一种基于九轴陀螺仪的电梯平台定位系统。

背景技术：

电梯现已作为一款重要的楼宇交通工具，而电梯的运行参数是电梯运转的重要参数，可获取电梯运行速、运行位置并确定当前是否正确停梯状态。因而对电梯的运行参数进行分析十分重要。现有电梯状态检测方式，仅仅定期进行人工检测等，无实时电梯轿厢系统加速度数据上报。或者仅针对轿厢内进行视音频数据采集，而没有关于电梯轿厢运行时的振动分析，精确判断电梯状态。

技术实现要素：

鉴于以上存在的技术问题，本发明用于提供一种基于九轴陀螺仪的电梯平台定位系统。

为解决上述技术问题，本发明采用如下的技术方案：

一种基于九轴陀螺仪的电梯平台定位系统，包括陀螺仪信号采集单元，陀螺仪实时分析计算单元，速度信息比较单元，振动信息比较单元，报警单元和大数据平台，其中：

所述陀螺仪采集单元包括安装在电梯轿厢的九轴陀螺仪的信息采集设备，用于采集固定于轿厢的陀螺仪信息，陀螺仪信息用于后续单元分析；

所述陀螺仪实时分析单元包括通用处理设备，根据陀螺仪实时数据进行加速度分析与振动分析，分别得到平台运行的实时速度信息与有人时加速度的振动频率和强度，以及平台日常运转的速度信息、振动频率和强度，并将相应信息送给大数据平台；

所述速度信息比较单元与振动信息比较单元包括通用处理设备，用于将陀螺仪实时分析单元得到的速度信息、振动信息，与平台参考信息进行比较，若达到报警阈值，或存在突发异常，则发送实时报警；

所述报警单元用于根据报警信息，发送信息给电梯维保部门。

优选地，所述陀螺仪实施分析单元的数据分析过程进一步包括：陀螺仪实时信息送入陀螺仪实时分析单元进行分析，利用姿态分解、离散变换，功率谱计算的方法分析出实时加速度信息以及加速度的振动频率、强度；进一步，通过数值积分、模态分解、短时频谱分析、模式识别的详细状态分析方法，深度分析得到实时速度信息与振动信息，根据平台日常运转状态时的加速度信息作为参考，并且将平台日常运转状态时的加速度信息综合得到包括电梯稳定运行速度、电梯稳定运行时加速度峰谷值、加速度振动频率、谐振频率、包络信号信息的平台参考信息。

优选地，九轴陀螺仪精确计算电梯姿态与运行信息，进一步包括以下步骤：

重力加速度归一化后的向量是[0，0，1]^t，转换到机体坐标系后为：

机体坐标系下测得的重力向量表示为[ax，ay，az]^t，误差向量表示为：

得到一个关于四元数q的最小二乘问题：

f(q)＝e

用梯度下降算法，矢量函数f(q)的梯度为：

j(q)^tf(q)

j(q)＝j(p)^tf(q)为：

于是

u表示梯度下降的收敛速度；

接下来把与陀螺仪测出来的数据融合，假设由微分方程求解的姿态四元数为qw，加速计测出来的四元数为qa，有：q＝α.qa+(1-α).qw

由于陀螺仪数据是发散的，所以α的最佳值是让陀螺仪解出来的四元数发散速度和加速计解出来的收敛速度相等，有：

β为陀螺仪的飘移速度，解出α的值为：当β和δt都接近0的时候，有代入q＝α.qa+(1-α)·qw，

有：

fg＝j(q)^tf(q)

考虑磁力计，原理一样，误差向量变成六维：

对应的雅各比矩阵和梯度算子都要加磁力计部分

单独对磁力计部分误差求雅各比矩阵：

于是新的雅各比矩阵就是：再与陀螺仪读数进行融合，将fg换成新的雅各比转置与误差函数即可。

采用本发明具有如下的有益效果：提出一种通过九轴陀螺仪的参数计算的方法，对应得到电梯平台运行的真实加速度计算得到实时运行速度值与实际运行位置，并可进一步根据加速度信息对电梯进行振动分析与位置分析，判断电梯的机械状态是否正常，以及电梯是否存在错位停梯。

附图说明

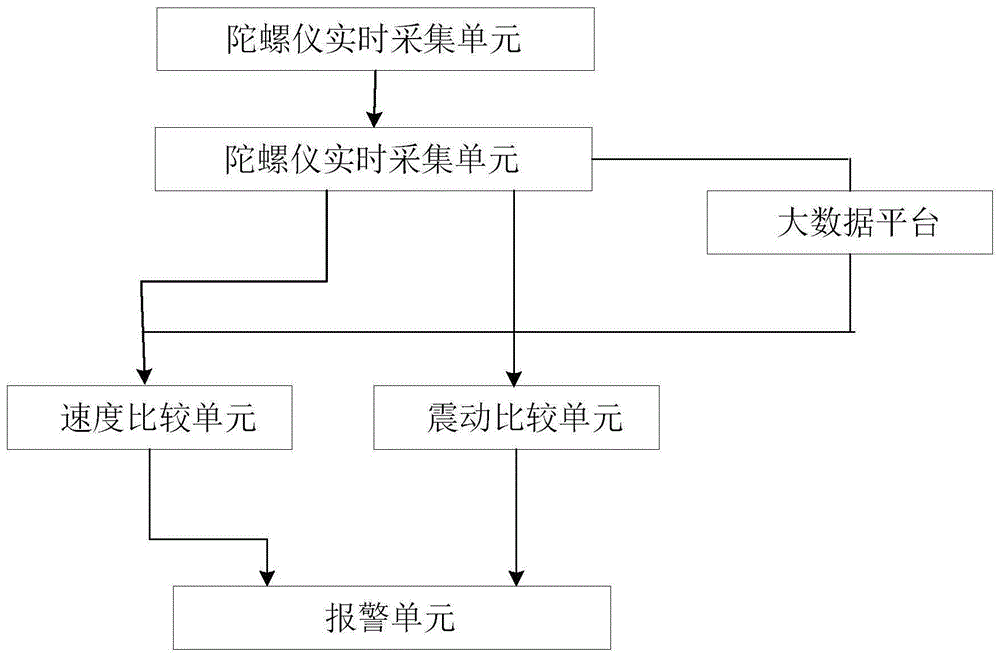
图1为本发明实施例的基于九轴陀螺仪的电梯平台定位系统的结构原理图。

具体实施方式

下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

参照图1，所示为本发明实施例的基于九轴陀螺仪的电梯平台定位系统的结构原理图，包括陀螺仪信号采集单元，陀螺仪实时分析计算单元，速度信息比较单元，振动信息比较单元，报警单元和大数据平台，其中：

陀螺仪采集单元包括安装在电梯轿厢的九轴陀螺仪的信息采集设备，用于采集固定于轿厢的陀螺仪信息，陀螺仪信息用于后续单元分析；

陀螺仪实时分析单元包括通用处理设备，根据陀螺仪实时数据进行加速度分析与振动分析，分别得到平台运行的实时速度信息与有人时加速度的振动频率和强度，以及平台日常运转的速度信息、振动频率和强度，并将相应信息送给大数据平台；

速度信息比较单元与振动信息比较单元包括通用处理设备，用于将陀螺仪实时分析单元得到的速度信息、振动信息，与平台参考信息进行比较，若达到报警阈值，或存在突发异常，则发送实时报警；

报警单元用于根据报警信息，发送信息给电梯维保部门。

具体应用实例中，陀螺仪实施分析单元的数据分析过程进一步包括：陀螺仪实时信息送入陀螺仪实时分析单元进行分析，利用姿态分解、离散变换，功率谱计算的方法分析出实时加速度信息以及加速度的振动频率、强度；进一步，通过数值积分、模态分解、短时频谱分析、模式识别的详细状态分析方法，深度分析得到实时速度信息与振动信息，根据平台日常运转状态时的加速度信息作为参考，并且将平台日常运转状态时的加速度信息综合得到包括电梯稳定运行速度、电梯稳定运行时加速度峰谷值、加速度振动频率、谐振频率、包络信号信息的平台参考信息。

具体应用实例中，九轴陀螺仪精确计算电梯姿态与运行信息，进一步包括以下步骤：

重力加速度归一化后的向量是[0，0，1]^t，转换到机体坐标系后为：

机体坐标系下测得的重力向量表示为[ax，ay，az]^t，误差向量表示为：

得到一个关于四元数q的最小二乘问题：

f(q)＝e

用梯度下降算法，矢量函数f(q)的梯度为：

j(q)^tf(q)

j(q)＝j(p)^tf(q)为：

于是

u表示梯度下降的收敛速度；

接下来把与陀螺仪测出来的数据融合，假设由微分方程求解的姿态四元数为qw，加速计测出来的四元数为qa，有：q＝α.qa+(1-α).qw

由于陀螺仪数据是发散的，所以α的最佳值是让陀螺仪解出来的四元数发散速度和加速计解出来的收敛速度相等，有：

β为陀螺仪的飘移速度，解出α的值为：当β和δt都接近0的时候，有代入q＝α.qa+(1-α).qw，

有：

fg＝j(q)^tf(q)

考虑磁力计，原理一样，误差向量变成六维：

对应的雅各比矩阵和梯度算子都要加磁力计部分

单独对磁力计部分误差求雅各比矩阵：

于是新的雅各比矩阵就是：再与陀螺仪读数进行融合，将fg换成新的雅各比转置与误差函数即可。

通过本发明实施例的基于九轴陀螺仪的电梯平台定位系统，一方面，通过九轴陀螺仪的参数精确计算，得到当前的实时加速度并计算得到当前运行速度与运行距离。另一方面，通过加速度进行进行振动分析，实时分析得到电梯平台运行时轿厢的振动信号属性(包括但不限于振动频率、强度等)，根据实时信号与平台录入的参考信号进行比较，综合判断后给出电梯状态是否正常。平台参考信息为大数据平台根据采集得到的电梯日常运转的振动信号综合给出。

应当理解，本文所述的示例性实施例是说明性的而非限制性的。尽管结合附图描述了本发明的一个或多个实施例，本领域普通技术人员应当理解，在不脱离通过所附权利要求所限定的本发明的精神和范围的情况下，可以做出各种形式和细节的改变。