一种基于大数据的电梯维修周期模型的计算方法与流程

1.本发明属于电梯维修领域；具体涉及一种基于大数据的电梯维修周期模型的计算方法。


背景技术：

2.随着现代城市建设的发展，我国电梯的数量在不断攀升。有数据显示，截止2018年底我国电梯的总量已经达到了490万台，占世界电梯总量的30％左右。如何加强电梯的维护保养，尽可能减少安全隐患，是现阶段物业管理部门以及电梯检修部门需要重点关注的问题。
3.目前在城市建设中，高层建筑中电梯是主要的物业设备，其运行维护费用占设备的较大成分。由于电梯为特种设备，如不选用厂家提供的配件，厂家将安全责任免责相要挟，如何能有效降低电梯在日常维修过程中的维保价格，保障和谐城市环境，加强物业设备的物理是一项重要工作。物业设备管理是一个内容繁多、技术复杂的综合性管理，是物业管理过程的重点，其中电梯、供配电系统、智能化系统、消防系统、给排水系统、供暖系统和人们的生活息息相关，不能出现任何差错。任何一个设备系统发生故障，都将造成居住者生活不便甚至混乱，维护设备成本的控制是服务好业主的一个重要手段。以电梯为例，物业管理公司负责设备的使用、运行及管理，电梯属于特种设备需要委托有资质专业或厂家售后服务专业化维修保养，如日常维护、一级保养、二级保养，中修、大修、故障维修、更新改造。物业管理公司应将三级保养制与计划预修制、状态维修相结合，对符合“浴缸型”电梯故障模式(符合磨损规律)的设备，定期做三级保养，定期进行中修、大修。


技术实现要素：

4.本发明提供了一种基于大数据的电梯维修周期模型的计算方法，维修的排班与调度是考虑了电梯各零件的使用状况进行维修，维修方式分为预防性维修和修复性维修两大类其目的是为了与普通排班更有效率的完成检修且保障电梯的各部分的零件可以保持良好的运行状况。
5.本发明通过以下技术方案实现：
6.一种基于大数据的电梯维修周期模型的计算方法，所述电梯维修周期方法包括以下步骤：
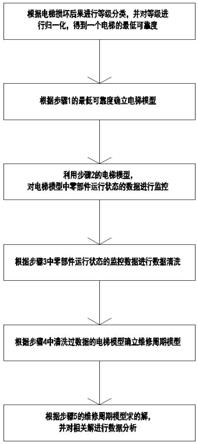
7.步骤1：根据电梯损坏后果进行等级分类，并对等级进行归一化，得到一个电梯的最低可靠度；
8.步骤2：根据步骤1电梯的最低可靠度确立电梯模型；
9.步骤3：利用步骤2的电梯模型，对电梯模型中零部件运行状态的数据进行监控；
10.步骤4：对步骤3中零部件运行状态的监控数据进行数据清洗；
11.步骤5：对步骤4中清洗过数据的电梯模型确立维修周期模型；
12.步骤6：根据步骤5的维修周期模型求得数据，并对相关数据进行数据分析。
13.进一步的，所述步骤1的电梯的最低可靠度具体为，最低可靠度是指工程实际可接受的设备或系统的最低可靠度:
[0014][0015]
其中，n为一个统计期内系统发生故障的次数，n为上述故障归一化的结果。
[0016]
进一步的，所述步骤2确立电梯模型具体包括以下步骤，
[0017]
步骤2.1：确立电梯零件模型；
[0018]
步骤2.2：对步骤2.1的电梯零件模型建立参数估计最优化模型；
[0019]
步骤2.3：利用em算法进行参数估计；
[0020]
步骤2.4：对步骤2.3的参数估计进行基于蒙特卡罗数据模拟。
[0021]
进一步的，所述步骤2.1确立电梯零件模型具体为，
[0022]
假设电梯的零件寿命服从韦氏分布，它的分布函数为，
[0023][0024]
其中λ为形状参数，k为尺度参数，k《1的值表示故障率随时间减小；k＝1的值表示故障率随时间是恒定的；k》1的值表示故障率随时间增加；
[0025]
如果一个总体由n个子体组成，对应的子体的累积分布函数是f1(t)，f2(t)，
…
，fn(t)，以及混合权ω1，ω2，
…
，ωn，则总体的累积分布函数f(t)为：
[0026]
f(t)＝ω1f1(t)+
…
+ω
nfn
(t)
[0027]
相应的混合模型密度分布函数f(t)为：
[0028]
f(t)＝ω1f1(t)+
…
+ω
nfn
(t)
[0029]
混合权ω1,ω2,
…
,ωn满足：
[0030][0031]
则设备寿命威布尔分布下的可靠度函数r(t)为，
[0032]
r(t)＝1-f(t)。
[0033]
进一步的，所述步骤2.2建立参数估计最优化模型具体为，
[0034]
选用两参数威布尔分布作为基函数，根据极大似然函数建立多重威布尔混合模型参数估计的优化模型：
[0035][0036]
式中：ti为第i个零件已经运行的时间，fj(ti)为第j个零件模型的密度分布函数，
ηj为第j个威布尔分布的尺度参数；βj为第j个威布尔分布的形状参数；ωj为第j个威布尔分布的权重系数；n为样本数据的个数；n为混合威布尔模型重数；为xi第i个样本量的取值。
[0037]
进一步的，所述步骤2.3利用em算法进行参数估计具体为，
[0038]
具体em算法步骤如下：
[0039]
步骤2.3.1：初始化参数
[0040]
步骤2.3.2：期望步根据下式迭代计算响应度γi：
[0041][0042]
其中，f(ti)是混合模型密度分布函数，是第j个威布尔分布的权重系数的k次方；
[0043]
步骤2.3.3：极大化步，根据下列方程迭代计算加权均值和方差：
[0044][0045]
步骤2.3.4：重复步骤2.3.2到步骤2.3.3直到极大似然函数值收敛，
[0046]
在步骤2.3.3中与存在关系方程式，
[0047][0048]
该方程显然为超越方程，难以得到解析解的形式；在em算法中，每一次迭代都要求解上述方程，令λ＝μ/σ，当λ＝0时，则有公式，
[0049][0050]
λ与β显然存在单调关系，由于函数关系复杂，采用径向基函数插值的数值方法根
据λ求解β，根据下式，
[0051][0052]
求解η。
[0053]
进一步的，所述步骤2.4基于蒙特卡罗数据模拟具体为，
[0054]
记电梯的n种零件的对应参数为(η1,β1),(η2,β2),
…
,(ηn,βn)，利用反变换法获取得到故障时间抽样为
[0055][0056]rk
∈r，r为乘同余组合发生器生成的随机数序列，
[0057]
假定电梯定期检查时间为t0，故障修复后，使用时间重新计算，累积到时间t0时，再做下次定检，模拟的基本步骤如下：
[0058]
步骤2.4.1：输入电梯零件的原始数据；
[0059]
步骤2.4.2：利用乘同余组合发生器构建[0,1]区间均匀随机数表；
[0060]
步骤2.4.3：针对每台发动机，从随机数表中顺序选取随机数，利用反变换法计算各个故障模式的随机故障时间g1,g2,
…
,gn，首次故障时间需大于发动机的已安全运行时间，否则需重新产生一组随机故障时间，直到均大于发动机已安全运行时间；
[0061]
步骤2.4.4：判断min{g1,g2,
…
,gn}是否小于定期检查时间t0，若是，则记录该故障gk，该故障模式发生次数累加1；
[0062]
步骤2.4.5：针对k零件故障，重新抽样故障时间gk；
[0063]
步骤2.4.6：重复步骤2.4.4：到步骤2.4.5：直到min{g1,g2,
…
,gn}超过t0；
[0064]
步骤2.4.7：遍历所有零件，每种零件模拟n次，并记录结果；
[0065]
步骤2.4.8：计算电梯中各零件发生的概率；
[0066]
步骤2.4.9：结合原始数据计算未来一段时间各零件故障可能发生的次数。
[0067]
进一步的，所述步骤4数据清洗具体为，
[0068]
步骤4.1：根据业务应用场景确定模型的初始值，创建多阶哈希表，并定义好存储在哈希表的标签节点数的数据结构；
[0069]
步骤4.2：确定标签的状态；当有标签数据《epc，time，ss》到来时，首先查询该标签在哈希表中是否存在其历史读取记录；若该标签不在哈希表中，则表示该标签处于unknown状态；如若标签在哈希表中，则在进一步确认标签的状态之前，需要先判断该标签是否处于有效的读取间隔内；若最近读取时间与最后一次的读取间隔超过有效时间阈值，则表示该标签之前的读取记录已失效，需要清空其读取记录，并将其视为首次读取的标签进行处理；若读取间隔仍然在有效的时间阈值之内，则根据哈希表该节点的state字段确定标签的状态；
[0070]
步骤4.3：定义标签状态转换的状态机，确定标签过滤的准则；
[0071]
步骤4.4：更新当前所有标签记录的平均读取信号强度，按照ss
avg
＝(ss
lastavg
*tagcnt+ss)/(tagcnt+1)方式进行计算，更新哈希表中该节点的最新读取时间和读取次数。
[0072]
进一步的，所述步骤5确立维修周期模型具体包括以下步骤，
[0073]
步骤5.1：建模假设及参数说明；
[0074]
每隔周期t进行更换，如果期间发生故障则进行故障更换，时间t为常数；cp：每次定时更换的总费用，包括预防性更换的费用和电梯不能使用带来的损失；cf：每次故障的总费用，包括故障更换费用和电梯不能使用带来的损失；c(t)：以周期t进行更换时，长期使用下的单位时间的费用；c(t，t)：以周期t进行更换时，在有限使用时间[0，t]内的期望费用；a(t)：以周期t进行更换时，长期使用条件下的平均可用度；tp：预防性更换所需的平均时间；tf：故障更换所需的平均时间；f(t)、r(t)和f(t)：产品首次故障时间累积分布函数、可靠度函数和故障密度函数，其中，当t＝0时表示产品处于新状态；
[0075]
步骤5.2：确立基于费用的电梯维修周期决策模型；
[0076]
根据更新过程的基本理论，长期使用下，电梯维修平均费用可表示为：
[0077][0078]
更新周期内总的期望费用＝预防性更换的费用*预防性更换的概率+故障更换的费用*故障更换的概率＝c
p
r(t)+cff(t)，
[0079][0080]
由于t
p
和tf相对于维修周期t来说很小，因此在费用模型中可以忽略；此时，期望更新周期长度变为平均费用可表示为，
[0081][0082]
如果令t
→
∞表明没有进行更换，所有的费用都是由故障引起的；此时，r(t)
→
0，单位时间的费用为，
[0083][0084]
为使更换经济有效，要合理地确定更换周期t以满足c(t)＜c(∞)；如果没有满足此条件的t值，则说明定时更换是无效的，此时不值得进行定时更换；
[0085]
步骤5.3：确立基于可靠度的维修周期决策模型；
[0086]
为了保证电梯的正常使用，或降低备用品发生故障的风险，有时需要寻找合适的更换周期t，以使得电梯的可用度最大和建立费用模型类似，能建立在长期使用情况下的可用度模型：
[0087][0088]
当t
→
∞时，即不进行预防性维修工作的时候，得到，
[0089]
a(t)
→
mttf/(mttf+tf)
[0090]
如果可用度是维修决策的主要因素，那么更换周期t应当满足，
[0091]
a(t)＞rr。
[0092]
本发明的有益效果是：
[0093]
基于不同原则的维修周期计算模型得出的维修周期可能不同，以维修费用最小为原则，可以保证在经济利益最大化的前提下基于历史数据完成对于电梯维修计划的安排，而以可靠度最高为原则，可以保证在安全性最大化的的前提下基于历史数据完成对于电梯维修计划的安排。
附图说明
[0094]
附图1本发明的方法流程图。
[0095]
附图2本发明标签的状态转换图。
[0096]
附图3本发明的清洗算法流程图。
[0097]
附图4本发明电梯零件的可靠度分布曲线图。
[0098]
附图5本发明的蒙特卡洛算法流程图。
[0099]
附图6电梯寿命原始数据图。
[0100]
附图7本发明电梯寿命数据分布的直方图。
[0101]
附图8本发明电梯寿命拟合曲线图。
具体实施方式
[0102]
下面将结合本发明实施例中的附图对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。
[0103]
一种基于大数据的电梯维修周期模型的计算方法，所述电梯维修周期方法包括以下步骤：
[0104]
步骤1：根据电梯损坏后果进行等级分类，并对等级进行归一化，等级为1的系数为1，等级为2的系数为1/29，等级为3的系数为1/300，得到一个电梯的最低可靠度；
[0105]
表1权重因子
[0106][0107]
步骤2：根据步骤1电梯的最低可靠度确立电梯模型；
[0108]
步骤3：利用步骤2的电梯模型，对电梯模型中零部件运行状态的数据进行监控；
[0109]
步骤4：对步骤3中零部件运行状态的监控数据进行数据清洗；
[0110]
步骤5：对步骤4中清洗过数据的电梯模型确立维修周期模型；
[0111]
步骤6：根据步骤5的维修周期模型求得数据，并对相关数据进行数据分析。
[0112]
进一步的，所述步骤1的电梯的最低可靠度具体为，最低可靠度是指工程实际可接
受的设备或系统的最低可靠度:
[0113][0114]
其中，n为一个统计期内系统发生故障的次数，n为上述故障归一化的结果。
[0115]
进一步的，所述步骤2确立电梯模型具体包括以下步骤，
[0116]
步骤2.1：确立电梯零件模型；
[0117]
步骤2.2：对步骤2.1的电梯零件模型建立参数估计最优化模型；
[0118]
步骤2.3：利用em算法进行参数估计；
[0119]
步骤2.4：对步骤2.3的参数估计进行基于蒙特卡罗数据模拟。
[0120]
进一步的，所述步骤2.1确立电梯零件模型具体为，
[0121]
假设电梯的零件寿命服从韦氏分布，它的分布函数为，
[0122][0123]
其中λ为形状参数，k为尺度参数，k《1的值表示故障率随时间减小；k＝1的值表示故障率随时间是恒定的；k》1的值表示故障率随时间增加；从而可以得到电梯零件的可靠度分布曲线，在许多情况下，一个总体可能由两个或多个子体组成；例如，由于设计、原材料、制造工艺等方面的差异，在不同情况下生产的产品可能有不同的寿命分布；
[0124]
如果一个总体由n个子体组成，对应的子体的累积分布函数是f1(t)，f2(t)，
…
，fn(t)，以及混合权ω1，ω2，
…
，ωn，则总体的累积分布函数f(t)为：
[0125]
f(t)＝ω1f1(t)+
…
+ω
nfn
(t)
[0126]
相应的混合模型密度分布函数f(t)为：
[0127]
f(t)＝ω1f1(t)+
…
+ω
nfn
(t)
[0128]
混合权ω1,ω2,
…
,ωn满足：
[0129][0130]
则设备寿命威布尔分布下的可靠度函数r(t)为，
[0131]
r(t)＝1-f(t)。
[0132]
进一步的，所述步骤2.2建立参数估计最优化模型具体为，
[0133]
选用两参数威布尔分布作为基函数，根据极大似然函数建立多重威布尔混合模型参数估计的优化模型：
[0134]
[0135]
式中：ti为第i个零件已经运行的时间，fj(ti)为第j个零件模型的密度分布函数，ηj为第j个威布尔分布的尺度参数；βj为第j个威布尔分布的形状参数；ωj为第j个威布尔分布的权重系数；n为样本数据的个数；n为混合威布尔模型重数；为xi第i个样本量的取值。
[0136]
进一步的，所述步骤2.3利用em算法进行参数估计具体为，利用贝叶斯随机分类的方法将不完全数据集随机分配到各独立分布，作为em算法的初始化方法；
[0137]
贝叶斯随机分类方法步骤如下：
[0138]
①
采用聚类分析法对不完整数据集进行分类，对每类数据进行威布尔分布参数的极大似然估计，作为各独立分布的先验分布参数，第j类样本数据对应的分布参数为(ηj,βj)；每类样本数据容量gi占总容量g的比值为各独立分布的权值ωi，即ωi＝gi/g；
[0139]
②
计算第i点在第j类独立分布的密度函数值f
ij
(xi)，并根据
[0140][0141]
归一化处理得到p
ij
，p
ij
表示第i个点隶属于第j个独立分布的后验概率；
[0142]
③
将第i点分配到第j类的后验概率区间为
[0143][0144]
每个点按照均匀分布产生随机概率ri，根据ri是否属于第j类后验概率区间判别第i点所属的分类；并根据当前样本分类更新每个独立分布相应的参数；
[0145]
④
根据
[0146][0147]
计算最大似然函数值，选似然函数值较大者为当前最优分类；
[0148]
⑤
重复
②
～
④
，直到最大似然函数值收敛或迭代次数结束。
[0149]
具体em算法步骤如下：
[0150]
步骤2.3.1：初始化参数
[0151]
步骤2.3.2：期望步根据下式迭代计算响应度γi：
[0152][0153]
其中，f(ti)是混合模型密度分布函数，是第j个威布尔分布的权重系数的k次方；
[0154]
步骤2.3.3：极大化步，根据下列方程迭代计算加权均值和方差：
[0155][0156]
步骤2.3.4：重复步骤2.3.2到步骤2.3.3直到极大似然函数值收敛，
[0157]
在步骤2.3.3中与存在关系方程式，
[0158][0159]
该方程显然为超越方程，难以得到解析解的形式；在em算法中，每一次迭代都要求解上述方程，令λ＝μ/σ，当λ＝0时，则有公式，
[0160][0161]
λ与β显然存在单调关系，由于函数关系复杂，采用径向基函数插值的数值方法根据λ求解β，根据下式，
[0162][0163]
求解η。
[0164]
进一步的，所述步骤2.4基于蒙特卡罗数据模拟具体为，
[0165]
记电梯的n种零件的对应参数为(η1,β1),(η2,β2),
…
,(ηn,βn)，利用反变换法获取得到故障时间抽样为，
[0166][0167]rk
∈r，r为乘同余组合发生器生成的随机数序列，
[0168]
假定电梯定期检查时间为t0，故障修复后，使用时间重新计算，累积到时间t0时，再做下次定检，模拟的基本步骤如下：
[0169]
步骤2.4.1：输入电梯零件的原始数据；
[0170]
步骤2.4.2：利用乘同余组合发生器构建[0,1]区间均匀随机数表；
[0171]
步骤2.4.3：针对每台发动机，从随机数表中顺序选取随机数，利用反变换法计算各个故障模式的随机故障时间g1,g2,
…
,gn，首次故障时间需大于发动机的已安全运行时间，否则需重新产生一组随机故障时间，直到均大于发动机已安全运行时间；
[0172]
步骤2.4.4：判断min{g1,g2,
…
,gn}是否小于定期检查时间t0，若是，则记录该故障gk，该故障模式发生次数累加1；
[0173]
步骤2.4.5：针对k零件故障，重新抽样故障时间gk；
[0174]
步骤2.4.6：重复步骤2.4.4：到步骤2.4.5：直到min{g1,g2,
…
,gn}超过t0；
[0175]
步骤2.4.7：遍历所有零件，每种零件模拟n次，并记录结果；
[0176]
步骤2.4.8：计算电梯中各零件发生的概率；
[0177]
步骤2.4.9：结合原始数据计算未来一段时间各零件故障可能发生的次数。
[0178]
进一步的，所述步骤4数据清洗具体为，
[0179]
针对标签数据存在的多读和大量冗余现象，根据一种基于有限状态机的清洗框架，提高了数据的处理效率。在定长的滑动窗口算法基础上进行改进，抛弃了传统清洗算法设置滑动窗口的方式，通过记录标签首次进入滑动窗口的时间、最近一次的读取时间、读取的次数等作为标签的状态记录，按照标签的状态对数据进行清洗。
[0180]
一个确定的有限状态机是由a＝(q，∑，δ，s，f)五元组构成的。本发明中五元组的实际意义如下：q表示非空的状态集合，由标签的各个状态组成；∑表示输入，即携带信息的标签流；δ表示转移函数δ:q
×
∑
→
q，根据输入和标签的状态确定状态的转换；s表示标签的初始状态，其中s∈q；f表示最终的标签状态集合，其中下面按照有限自动机的五元组阐述本发明的清洗算法的思想。
[0181]
1)确定标签的状态集合q和初始状态s
[0182]
通过对标签流的研究，提出将标签的整个读写过程定为unknown状态、captured状态和observed状态3种状态，即标签的状态集合q＝{unknown，captured，observed}。其中，unknown表示标签不在读取区域之内，无法知道标签的信息，处于未知状态中；
[0183]
captured表示标签首次被捕捉后的状态，意味着标签已经进入读取区域，但根据当前的信息无法确定该标签属于正常还是异常数据；observed则表示标签在读取区域中，已经确认被读取到，是可靠数据。标签的初始状态是指该标签还未被捕捉的时候，处于未知状态，s＝{unknown}。
[0184]
2)确定标签流的组成∑
[0185]
从阅读器传输到中间件的rfid原始数据，一般可认为每个标签记录都是由一个三元组《epc，location，time》组成。其中，epc代表标签独一无二的id；location表示阅读器放置的地方，即标签被捕获的位置；time则表示阅读器检测到该标签的时间。本发明的数据清洗算法中并没有针对标签的位置信息location作任何处理，因此并不需要该特性。本课题在研究标签的读取过程的数据后，提出在这个三元组中用标签的读取信号强度(signal strength)代替标签的位置信息，作为标签的读写特征，用ss表示，取值范围0～100。值越大，表明信号越强。由于物联网技术本身的内在敏感性，信号强度往往与货物的性质(金属非金属、液体等)标签所贴的商品位置及与阅读器所处的位置相关。越贴近阅读器信号越
强，而与阅读器距离越远，信号越弱。标签的读取信号强度可以更加贴切反映标签读取过程的特征，因此本发明的标签数据均可以为是以《epc，time，ss》三元组形式存在的。
[0186]
3)确定标签在状态机转换机制δ:q
×
∑
→q[0187]
标签的状态转换机制是清洗算法的核心，标签的转换即数据清洗的过程。为了实现快速查询标签的读取记录，将使用多阶哈希表作为存储标签读取记录的数据结构。本发明算法主要根据在有效的时间内以标签的读取次数和读取信号强度确定标签的状态转换。标签的读写次数是表明标签读取过程的一个重要特征，如果读取次数较多，那么有理由相信该数据不是偶然读到，属于正常数据的可能性非常高。在rfid数据分析中发现，无论应用的场景怎样变化，无论是快速通道还是库存盘点，大部分的rfid标签数据的读取信号强度都趋近于高斯分布。而标签多读现象产生的原因多是标签刚好经过阅读器的区域，具有与阅读器距离较远、读取强度较低等特点。因此，本发明使用标签读取信号强度的目的在于增加一个特征确定数据是否是可靠数据，减少单一特征可能造成的清洗误差。同时，为了适应更多的应用场景，避免提前预设信号强度阈值，本发明在清洗过程中记录所有标签的平均读取强度ss
avg
：
[0188][0189]
其中totalcnt表示标签的总的读取数。根据中心极限定理，当某标签的功率超过当前的平均值，便有理由相信该标签是正常数据，从而可以确保即使在标签的读写次数达不到阈值烦人情况下，仍然可以判定该数据是正常数据，减少了数据清洗的错误率。
[0190]
步骤4.1：根据业务应用场景确定模型的初始值，依照上述方法创建多阶哈希表，并定义好存储在哈希表的标签节点数的数据结构；
[0191]
步骤4.2：确定标签的状态；当有标签数据《epc，time，ss》到来时，首先查询该标签在哈希表中是否存在其历史读取记录；若该标签不在哈希表中，则表示该标签处于unknown状态；如若标签在哈希表中，则在进一步确认标签的状态之前，需要先判断该标签是否处于有效的读取间隔内；若最近读取时间与最后一次的读取间隔超过有效时间阈值，则表示该标签之前的读取记录已失效，需要清空其读取记录，并将其视为首次读取的标签进行处理；若读取间隔仍然在有效的时间阈值之内，则根据哈希表该节点的state字段确定标签的状态；
[0192]
步骤4.3：如图所示，定义标签状态转换的状态机，确定标签过滤的准则；
[0193]
当标签处于unknown状态时，将其加入多阶哈希表中，设定其读取次数、读取时间。此时，考虑其信号读取强度是否超过当前的标签记录的平均读取强度ss
avg
。若超过，则直接设置状态为observed状态，作为干净数据加入队列queue中，供上层业务系统调用；若其读取的信号强度小于平均值，则转入captured状态。
[0194]
当标签处于captured状态时，更新其节点数据，考虑其读取次数和其信号读取强度是否超过当前的标签记录的平均读取强度ss
avg
，若超过平均值或其读取次数刚好到达有效读取的阈值，标签将转为observed状态，标签值则作为过滤后的干净数据加入队列queue中；否则，该标签仍然处于captured态。
[0195]
当标签处于observed状态时，新的读取记录作为冗余数据过滤掉。在实际应用中，绝大多数标签均处于该状态。
[0196]
步骤4.4：更新当前所有标签记录的平均读取信号强度，按照ss
avg
＝(ss
lastavg
*tagcnt+ss)/(tagcnt+1)方式进行计算，更新哈希表中该节点的最新读取时间和读取次数。
[0197]
进一步的，所述步骤5确立维修周期模型具体包括以下步骤，
[0198]
步骤5.1：建模假设及参数说明；
[0199]
每隔周期t进行更换，如果期间发生故障则进行故障更换，时间t为常数；cp：每次定时更换的总费用，包括预防性更换的费用和电梯不能使用带来的损失；cf：每次故障的总费用，包括故障更换费用和电梯不能使用带来的损失；c(t)：以周期t进行更换时，长期使用下的单位时间的费用；c(t，t)：以周期t进行更换时，在有限使用时间[0，t]内的期望费用；a(t)：以周期t进行更换时，长期使用条件下的平均可用度；tp：预防性更换所需的平均时间；tf：故障更换所需的平均时间；f(t)、r(t)和f(t)：产品首次故障时间累积分布函数、可靠度函数和故障密度函数，其中，当t＝0时表示产品处于新状态；
[0200]
步骤5.2：确立基于费用的电梯维修周期决策模型；
[0201]
根据更新过程的基本理论，长期使用下，电梯维修平均费用可表示为：
[0202][0203]
更新周期内总的期望费用＝预防性更换的费用*预防性更换的概率+故障更换的费用*故障更换的概率＝c
p
r(t)+cff(t)，
[0204][0205]
由于t
p
和tf相对于维修周期t来说很小，因此在费用模型中可以忽略；此时，期望更新周期长度变为平均费用可表示为，
[0206][0207]
如果令t
→
∞表明没有进行更换，所有的费用都是由故障引起的；此时，r(t)
→
0，单位时间的费用为，
[0208][0209]
为使更换经济有效，要合理地确定更换周期t以满足c(t)＜c(∞)；如果没有满足此条件的t值，则说明定时更换是无效的，此时不值得进行定时更换；
[0210]
步骤5.3：确立基于可靠度的维修周期决策模型；
[0211]
为了保证电梯的正常使用，或降低备用品发生故障的风险，有时需要寻找合适的更换周期t，以使得电梯的可用度最大和建立费用模型类似，能建立在长期使用情况下的可用度模型：
[0212][0213]
当t
→
∞时，即不进行预防性维修工作的时候，得到，
[0214]
a(t)
→
mttf/(mttf+tf)
[0215]
如果可用度是维修决策的主要因素，那么更换周期t应当满足，
[0216]
a(t)＞rr。
[0217]
进一步的，所述步骤6对相关数据进行数据分析具体为，
[0218]
寿命服从两参数威布尔分布并求得形状参数λ＝4.07，尺度参数k＝238.59，进行数据模拟得到的原始1000个数据样本，进行数据处理后得到数据分布的直方图
[0219]
对于原始数据利用em算法进行参数估计，估计后得到的形状参数为λ＝4.2434，尺度参数为k＝241.2584，
[0220][0221]
取相关参数cp＝100；cf＝300；tp＝1(h)；tf＝2(h)，取维修周期t步长15d，tmin＝100d，tmax＝325d，分别代入
[0222][0223][0224]
计算可得，
[0225]
表2 c(t)、a(t)、g(t)值与维修周期t关系
[0226]
tc(t)a(t)g(t)1001.062 950.989 760.931 141151.007 770.990 380.982 741300.966 160.990 901.025 591450.937 500.991 311.057 391600.920 920.991 621.076 771750.915 410.991 851.083 501900.919 710.992 011.078 602050.932 360.992 091.064 072200.951 660.992 121.042 512350.975 830.992 111.016 682501.003 020.992 070.989 082651.031 480.991 990.961 722801.059 720.991 910.936 022951.086 590.991 830.912 803101.086 590.991 770.892 423251.133 520.991 770.874 88
[0227]
若在某一时期内发生故障级别1、2、3的次数分别为14，135，25次则最低可靠度为：
[0228][0229]
则故障率函数为，
[0230][0231]
为使得电梯设备维修周期达到更好的综合效果最佳维修周期的制定需同时考虑经济性和可用度要求。考虑寻求某个维修周期t，使得目标函数g(t)取得最大值，
[0232][0233]
当g(tg)＝max g(t)时，tg即为综合考虑两原则的设备最佳维修周期，
[0234]
代入
[0235][0236]
s.t.r(t)≥rr[0237]
求得，c(175)＝minc(t)＝0.91541元/天，故以费用最小为原则最佳维修周期为t＝175天。
[0238]
a(220)＝maxa(t)＝0.99212，因此以可用度最大为原则最佳预防维修周期t＝220天。
[0239]
g(t)值反应了设备取维修周期t时的综合效果，g(175)＝maxg(t)＝1.0835，因此最佳预防维修周期为t＝175天。
[0240]
基于不同原则的维修周期计算模型得出的维修周期可能不同，以维修费用最小为原则，可以保证在经济利益最大化的前提下基于历史数据完成对于电梯维修计划的安排，而以可靠度最高为原则，可以保证在安全性最大化的的前提下基于历史数据完成对于电梯维修计划的安排。