一种面向物料传输平台的运动学建模策略与路径规划方法

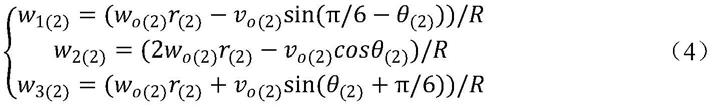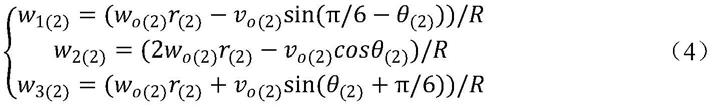
1.本发明涉及物流传输，特别是一种面向物料传输平台的运动学建模策略与路径规划方法。


背景技术：

2.随着互联网技术的高速发展以及智能化和信息化技术在生产与物流中的快速普及为传统物流行业注入了“智能”基因，但是在生产实际中大多数传输系统仍然停留在人工或者半自动传输阶段，整体自动化水平并不高；同时，全向轮因其相对于其他轮式结构的无法代替的独特特性，具有广大的发展前景，全向轮的物流传输机构研究越来越成为物流传输领域的一个热点；不同的运动学建模策略适用于不同的系统；传统蚁群算法与人工势场法在路径规划过程中易出现收敛速度慢、陷入局部极小值等问题。
3.罗继军提出了一种双链防滑格挡式分拣机，通过链轮与链条啮合作用使货物稳定传输，但当某个啮合环节出现故障时，货物会造成堆积，严重影响分拣效率。倪桥设计了一种自动化翻盘式分拣机，该系统分拣方向固定，灵活性低，且采用翻盘形式，货物尺寸与重量存在限制，否则易造成货物的碰撞损坏。曹现刚采用多机械臂协同控制的策略对带式输送机上的货物进行分拣，多机械臂的使用增加了系统成本，若某个机械臂发生故障，其他机械臂的负担将加重，易导致系统崩溃。王洪斌提出了一种改进的a*算法与动态窗口法相结合的混合算法，该方法虽然实现了机器人的路径规划，但由于采用多目标运输的方式，算法复杂程度相应提高，时效性较低。李孟锡提出一种基于启发信息扩展节点的a*算法与混合蚁群算法相结合的路径规划方法，但没有对存在障碍物的情况深入研究，算法的适应性不高。何少佳将粒子群算法与蚁群算法相结合，降低前期蚂蚁搜索路径的时间，但在路径寻优能力上还有待改进，且算法运行后期容易陷入局部极小值。
4.通过现有技术的研究，可以分析出大多数传输系统难以满足多样化的传输需求，传输效率不高且一次性投入成本巨大；在路径规划方面，大多数改进后的路径规划算法仍会出现搜索结果不稳定、易陷入局部极小值等问题，不能保证路径最优。


技术实现要素：

5.发明目的：本发明的目的是提供一种面向物料传输平台的运动学建模策略与路径规划方法，从而实现全方位的自动化传输且工作台面积与高度能满足不同的传输需求，提高路径规划算法的收敛速度，降低陷入局部极小值概率，缩短传输路径，减少传输时间。
6.技术方案：本发明提供了一种物料传输平台，所述工作平台嵌入式安装有万向轮的六边形模块体，可无限拼接扩展，工作台面板随之扩大或缩小，模块体与工作台面通过连接件相接；所述工作台上的六边形单元模块盒上的轮系呈正三角布局，模块盒呈类蜂巢排列布局方式；所述运动学模型的实时切换使传输更加平稳；所述物料传输系统采用改进蚁群算法与人工势场法的路径规划方法，可使算法搜索过程更具有针对性，提高收敛速度，降低陷入局部极小值概率，相应提高传输平台的传输效率。
7.模块盒下表面内侧固定若干连接杆，用于固定模块体上表面嵌入的电机；所述模块盒上表面开有若干通过螺栓连接的安装孔，用于模块的安装与拆卸；所诉模块盒上物料尺寸固定，表面积不大于模块盒表面积，且能覆盖三个全向轮。
8.工作台下方装有六个高度可调节的支架，通过法兰连接板与工作台面板连接，位于四角的支架下方装有可自锁的滚轮，实现整个传输平台的位置调整。
9.控制系统采用stm32单片机作为主控芯片，上位机控制器通过can总线协议与各个模块体控制器进行通讯，工作台装有用于连接物联网的wi-fi模块，可在移动终端上远程监测物料传输过程；待传输物料贴有rfid电子标签，可利用平台入口处的rfid接收器提取该传输物料的地理位置信息。
10.本发明提供了一种面向物料传输平台的运动学建模策略与路径规划方法，其控制方法，包括以下步骤：
11.(1)采用多运动学建模策略，完成控制用运动学模型库的建立；
12.(2)上位机中配置总单元模块数目，包括六边形模块的边长及x、y轴方向数目，规定物料传输速度；
13.(3)通过rfid获取传输物料的的地理位置信息，并反馈给上位机；
14.(4)采用改进蚁群算法规划全局传输路径；
15.(5)采用改进人工势场法规划局部传输路径；
16.(6)在规划后的传输路径上，实现多运动学模型的动态切换，并解算出相关全向轮对应的转速及转向。
17.该物料传输平台通过wi-fi模块接入物联网，可通过移动终端对物料整个传输过程进行远程监测。
18.所述步骤(2)中，对两个模块参与传输时相邻轮子存在不对称分布的情况下建立运动学模型的步骤为：
19.(2.1)选取中心点o
(l)
建立世界坐标系，x
(l)
轴从下到上依次增大，y
(l)
轴从左到右依次增大，v
ox(l)
表示v
o(l)
在x
(l)
轴上的分速度，v
oy(l)
表示v
o(l)
在y
(l)
轴上的分速度，v
o(l)
表示点o
(l)
的线速度，w
o(l)
表示点o
(l)
的角速度，θ
(l)
表示v
o(l)
与x
(l)
轴夹角，其中l＝1,2,3，表示物料传输时参与的模块个数；
20.(2.2)建立三个全向轮速度v
1(2)
、v
2(2)
、v
3(2)
在本体坐标系x
(2)
轴、y
(2)
轴的速度分量v
x(2)
、v
y(2)
与世界坐标系中v
ox(2)
与v
oy(2)
的关系：
[0021][0022][0023][0024]
式中r
(2)
表示v
y(2)
方向与o
(2)
点的垂直距离，为常量；
[0025]
(2.3)由v
qy(2)
＝w
q(2)
r(q＝1,2,3)解算出各轮转速w
q(2)
与角速度w
o(2)
之间的关系式：
[0026][0027]
式中r表示全向轮的等效半径；
[0028]
(2.4)将公式(4)写成矩阵形式，即逆运动学方程：
[0029][0030]
所述步骤(2)中，对三个模块参与传输时相邻轮子都不对称分布的情况下建立运动学模型的步骤为：
[0031]
逆运动学方程：
[0032][0033]
基于3个全向轮的转速计算点o
(l)
的速度，形成正运动学方程：
[0034][0035]
所述步骤(4)改进蚁群算法的全局路径规划具体流程如下：
[0036]
(4.1)环境建模：地形图采用矩形栅格化的0/1方式，0表示可通过位置，1表示障碍物位置，左上角方块为起始点位置，右下角方块为目标点位置，建立直角坐标系：x轴、y轴数值分别从左到右、从上到下依次递增，自定义栅格为20
×
20比例，即x＝y＝i，其中i∈[1,20]且i∈n，并放置一代蚂蚁，其中当某一六边形模块发生故障时，将其视为障碍物用1表示，若障碍物不满一个栅格仍视为占满一个栅格；
[0037]
(4.2)改进蚁群算法的启发函数：通过引入当前模块位置与下一模块位置之间的距离和下一模块位置与目标模块位置距离之和，并且加入权重因子λ1和λ2对启发函数进行改进，使得算法搜索过程更有针对性，并降低陷入局部极小值概率，具体改进方法如下：
[0038][0039][0040]
式中m为物料当前模块位置，n为物料可能传输的下个模块位置，d为物料传输目标点位置，η
′
mn
为改进后的距离启发函数，d
nd
为n与d之间的欧几里得距离，且考虑到本平台结构的独特性，设定λ1+λ2＝2，且λ1、λ2》0；
[0041]
(4.3)改进蚁群算法的信息素启发因子与距离期望函数因子，考虑到早期路径中信息素含量过低，增加了蚂蚁搜索路径的盲目性，而后期由于信息素积累过多，又缩小了路径的可选择范围，导致算法陷入局部最优，信息素启发因子与距离期望函数因子在不同时刻重要程度的不同，设计因子自适应更新策略，具体改进方法如下：
[0042][0043][0044]
式中k为算法总迭代次数，k为当前迭代次数，α为初始信息素启发因子，β为初始距离期望函数因子，其中u为常量，考虑到本平台结构的独特性，设定u＝2e/3。
[0045]
(4.4)确定当前可行模块道路集，引入轮盘赌算法建立并更新传输模块间的优化概率模型，优化后的概率模型具体表达式为：
[0046][0047]
式中aj表示物料下一步可达到的模块集合，为优化后的传输路径上的信息素浓度，为改进后的距离启发函数；
[0048]
(4.5)更新传输路径上的信息素含量，具体表达式为：
[0049]
τ
mn
(t+1)＝(1-ρ)τ
mn
(t)+δτ
mn
(t)
ꢀꢀꢀꢀꢀ
(13)
[0050][0051][0052]
式中ρ为信息素挥发系数，δτ
mn
为两相邻模块释放的信息素的和，为两相邻模块的信息素增量，lj为蚂蚁j经过的路径长度，q为信息素增强系数；
[0053]
(4.6)计算当前迭代得到的可行解，并与前代所得到的可行解进行对比，记录最优解，待迭代次数结束后，规划出物料传输的全局最短路径。
[0054]
在局部路径规划中，增设模糊斥力点以改进传统人工势场法，额外产生的斥力可使物料逃离局部极小值点，具体模糊斥力点的增设过程如下：
[0055]
(5.1)首先以物品中心r为圆心，障碍物作用的最大距离ρ0为半径画圆r1；构造同时经过距离r最近障碍物点f与起点o的直线l1；记录l1与x轴的夹角θ；判定落在圆r1内的障碍物个数c；若c＝1执行步骤(5.2)，若c＝i(i＝2,3,4...)则执行步骤(5.3)；
[0056]
(5.2)障碍物个数为1个；求出物品与f之间距离l1；随后以r为圆心，l1为半径画圆r2；将l1以圆心r为基准，正或逆时针旋转θ角度构造直线l2；l2与圆r2的交点中距离f较远的节点为模糊斥力点q；
[0057]
(5.3)障碍物个数为多个；记录距离物品中心r最近的2个障碍物之间的距离l2、之间的中心点f及物品轮廓最大尺寸h(已知参数)；同时求出f与r之间的距离l
min
；以r为圆心，l
min
为半径画圆r3；
[0058]
若h《l2，则构造经过f与r的直线l3，l3与圆r3的交点中距离f较远的节点为模糊斥力点q；
[0059]
若h≥l2，则构造经过f与r的直线l4，将l4以圆心r为基准，正或逆时针旋转θ角度构造直线l5；l5与圆r3的交点中距离f较远的节点为模糊斥力点q。
[0060]
一种计算机存储介质，其上存储有计算机程序，该计算机程序被处理器执行时实现上述的一种面向物料传输平台的运动学建模策略与路径规划方法。
[0061]
一种计算机设备，包括储存器、处理器及存储在存储器上并可在处理器上运行的计算机程序，所述处理器执行所述计算机程序时实现上述的一种面向物料传输平台的运动学建模策略与路径规划方法。
[0062]
有益效果：与现有技术相比，本发明具有如下优点：
[0063]
1、工作台可根据物料传输量的需求扩展且高度可调，模块定位准确，系统适用于不同环境，实现全自动化，装有用于连接物联网平台的wi-fi模块，可在移动终端上远程监测，装有rfid电子标签，自动提取传输物料的地理位置信息，实现非接触式的数据通信；
[0064]
2、上位机中实现不同运动学模型的实时切换，并解算各个轮子速度及转向，使传输更加平稳；
[0065]
3、路径规划方面，提出改进的蚁群算法与人工势场法，相比传统算法，提高收敛速度，降低陷入局部极小值概率，相应缩短了传输路径，减少了传输时间。
附图说明
[0066]
图1为传输平台的整体结构示意图；
[0067]
图2为全向轮模块体结构示意图；
[0068]
图3为控制方法的具体流程图；
[0069]
图4为两个模块参与传输时相邻轮子存在不对称分布情况下的运动学模型解算示意图；
[0070]
图5为三个模块参与传输时相邻轮子都不对称分布情况下运动学模型解算示意图；
[0071]
图6为本发明改进蚁群算法下的全局路径规划具体流程图；
[0072]
图7为单个障碍物时模糊斥力点示意图；
[0073]
图8为多个障碍物时模糊斥力点示意图，其中图8a为h《l2时的示意图，图8b为h≥l2时的示意图；
[0074]
图9为本发明传统蚁群算法与改进蚁群算法的运动轨迹对比图，其中图9a为传统蚁群算法运动轨迹，图9b为改进蚁群算法运动轨迹；
[0075]
图10为本发明传统蚁群算法与改进蚁群算法的收敛曲线对比图；
[0076]
图11为改进前后人工势场法局部最优时路径规划对比图，其中图11a为h《l2时的示意图，图11b为h≥l2时的示意图。
具体实施方式
[0077]
下面结合附图对本发明的技术方案作进一步说明。
[0078]
如图1-2所示，本发明的面向物料传输平台的运动学模型包括装有全向轮的六边形模块体1、工作台面板2、连接件3、伸缩杆支架4、wi-fi模块5和自锁滚轮6，工作台由多个六边形模块体1拼接构成，平台可无限扩展拼接，六边形模块体1上有用于与连接件3连接时定位的开槽，连接件3上设有用于与模块盒11连接时定位的缺口，当将六边形模块体1安装到工作台面板2上时，将开槽与连接件3上的缺口插接，模块盒11的沿圆周方向的开口两侧
各设有两个安装孔16，六边形模块体1与连接件3通过螺栓连接，定位过程简便，定位准确且能够防止六边形模块体1的上下窜动，伸缩杆支架4通过法兰板与工作台面板2连接，伸缩杆支架4可伸缩，用于调节工作台的高度，wi-fi模块5可连接物联网平台，在移动终端上远程监测，自锁滚轮6使整个平台具有良好的移动性与稳定性。
[0079]
六边形模块体1包括模块盒11、连接杆12、托盘13、rfid模块14、全向轮15和安装孔16，模块盒11内侧与连接杆12的顶端固定连接，三根连接杆12的底端固定有托盘13，六边形模块体1中心装有rfid模块14，可自动提取传输物料的地理位置信息，实现非接触式的数据通信。
[0080]
如图3所示，本发明的控制方法具体流程为：
[0081]
采用多运动学建模策略，完成控制用运动学模型库的建立；上位机中配置总单元模块数目，包括六边形模块的边长及x、y轴方向数目，规定物料传输速度；通过rfid获取传输物料的的地理位置信息，并反馈给上位机；采用改进蚁群算法规划全局传输路径；采用改进人工势场法规划局部传输路径；在规划后的传输路径上，实现多运动学模型的动态切换，并解算出相关全向轮对应的转速及转向。该物料传输平台通过wi-fi模块接入物联网，可通过移动终端对物料整个传输过程进行远程监测。
[0082]
如图4所示，对两个模块参与传输时相邻轮子存在不对称分布情况下建立运动学模型：
[0083]
三个全向轮速度v
1(2)
、v
2(2)
、v
3(2)
在本体坐标系x
(2)
轴、y
(2)
轴的速度分量v
x(2)
、v
y(2)
与世界坐标系中v
ox(2)
与v
oy(2)
的关系式如下：
[0084][0085][0086][0087]
式中r
(2)
表示v
y(2)
方向与o
(2)
点的垂直距离，为常量；
[0088]
由v
qy(2)
＝w
q(2)
r(q＝1,2,3)解算出各轮转速w
q(2)
与角速度w
o(2)
之间的关系式：
[0089][0090]
式中r表示全向轮的等效半径；
[0091]
上式写成矩阵形式，即逆运动学方程：
[0092][0093]
如图5所示，对三个模块参与传输时相邻轮子都不对称分布的情况下建立运动学模型：
[0094]
逆运动学方程：
[0095][0096]
基于3个全向轮的转速计算点o
(l)
的速度，形成正运动学方程：
[0097][0098]
如图6所示，本发明的改进蚁群算法流程图：
[0099]
初始化参数包括环境建模：地形图采用矩形栅格化的0/1方式，0表示可通过位置，1表示障碍物位置，左上角方块为起始点位置，右下角方块为目标点位置，建立直角坐标系：x轴、y轴数值分别从左到右、从上到下依次递增，自定义栅格为20
×
20比例，即x＝y＝i，其中i∈[1,20]且i∈n，并放置一代蚂蚁，其中当某一六边形模块发生故障时，将其视为障碍物用1表示，若障碍物不满一个栅格仍视为占满一个栅格；
[0100]
通过引入当前模块位置与下一模块位置之间的距离和下一模块位置与目标模块位置距离之和，并且加入权重因子λ1和λ2对启发函数进行改进，使得算法搜索过程更有针对性，并降低陷入局部极小值概率，具体改进方法如下：
[0101][0102][0103]
式中m为物料当前模块位置，n为物料可能传输的下个模块位置，d为物料传输目标点位置，η
′
mn
为改进后的距离启发函数，d
nd
为n与d之间的欧几里得距离，且考虑到本平台结构的独特性，设定λ1+λ2＝2，且λ1、λ2》0；
[0104]
考虑到早期路径中信息素含量过低，增加了蚂蚁搜索路径的盲目性，而后期由于信息素积累过多，又缩小了路径的可选择范围，导致算法陷入局部最优，设计因子自适应更新策略，具体改进方法如下：
[0105][0106][0107]
式中k为算法总迭代次数，k为当前迭代次数，α为初始信息素启发因子，β为初始距离期望函数因子，其中u为常量，考虑到本平台结构的独特性，设定u＝2e/3；
[0108]
确定当前可行模块道路集，引入轮盘赌算法建立并更新传输模块间的优化概率模型，优化后的概率模型具体表达式为：
[0109]
[0110]
式中aj表示物料下一步可达到的模块集合，为优化后的传输路径上的信息素浓度，为改进后的距离启发函数；
[0111]
判断一代蚂蚁是否完成路径，若没完成回到候选道路集确定阶段，若完成，选出一代蚂蚁中的最佳路径；
[0112]
一代蚂蚁最佳路径确定后，判断是否达到最大迭代次数，若没达到则更新传输路径上的信息素含量，具体表达式为：
[0113]
τ
mn
(t+1)＝(1-ρ)τ
mn
(t)+δτ
mn
(t)
[0114][0115][0116]
式中ρ为信息素挥发系数，δτ
mn
为两相邻模块释放的信息素的和，为两相邻模块的信息素增量，lj为蚂蚁j经过的路径长度，q为信息素增强系数；
[0117]
若达到最大迭代次数则选择最佳路径，完成最短全局路径规划。
[0118]
如图7所示，本发明的单个障碍物时模糊斥力点示意图：
[0119]
以物品中心r为圆心，障碍物作用的最大距离ρ0为半径画圆r1；构造同时经过距离r最近障碍物点f与起点o的直线l1；记录l1与x轴的夹角θ；判定落在圆r1内的障碍物个数c；
[0120]
障碍物个数为1个，求出物品与f之间距离l1；以r为圆心，l1为半径画圆r2；将l1以圆心r为基准，正或逆时针旋转θ角度构造直线l2。l2与圆r2的交点中距离f较远的节点为模糊斥力点q，图中为逆时针旋转。
[0121]
如图8所示，本发明的多个障碍物时模糊斥力点示意图：
[0122]
障碍物个数为多个，记录距离物品中心r最近的2个障碍物之间的距离l2、之间的中心点f及物品轮廓最大尺寸h(已知参数)；同时求出f与r之间的距离l
min
；以r为圆心，l
min
为半径画圆r3。
[0123]
如图8(a)所示，若h《l2，则构造经过f与r的直线l3，l3与圆r3的交点中距离f较远的节点为模糊斥力点q。
[0124]
如图8(b)所示，若h≥l2，则构造经过f与r的直线l4，将l4以圆心r为基准，正或逆时针旋转θ角度构造直线l5。l5与圆r3的交点中距离f较远的节点为模糊斥力点q，如图8(b)所示，图中为逆时针旋转。
[0125]
如图9所示，本发明的传统蚁群算法与改进蚁群算法的运动轨迹对比图：
[0126]
传统蚁群算法运动轨迹拐点较多，13个，运行时间约为13.2秒，且在图中坐标(8,10)处，从两障碍物中心穿越，在本传输平台上属于不合理路径，应当排除；相比其缺点，本发明改进的蚁群算法运动轨迹拐点较少，7个，运行时间约为8.1秒，拐点数目减少46.1％，搜索效率提高38.7％。
[0127]
如图10所示，本发明的传统蚁群算法与改进蚁群算法的收敛轨迹对比图：
[0128]
传统蚁群算法收敛曲线，波动较大，收敛速度慢且在60迭代次数左右时才趋于稳定，同时该算法出现陷入局部极小值情况，最短路径约为35；相比其缺点，本文发明改进的
蚁群算法，波动较小，收敛速度快且在31迭代次数左右时完成收敛，且最短路径约为30，使全局路径的长度缩短14.3％，收敛速度提升51.7％，整个传输平台的传输效率随之提高。
[0129]
如图11(a)可知，当物品陷入局部最优且h《l2时，引入模糊斥力点使物品从两障碍物间穿过，逃离局部极小值点，同时也能使物品运输避障的路径达到最优，即所经过的路径最短。
[0130]
由图11(b)可知，同等条件下当h≥l2时，物品会从障碍物一侧绕过，有效避开障碍物。