基于中央空调系统动态仿真平台的智能优化控制方法

1.本发明涉及一种基于中央空调系统动态仿真平台的智能优化控制方法，具体适用于通过智能建模降低中央空调能耗。


背景技术：

2.随着我国经济的快速发展，我国的资源问题和环境问题都日益突出，节能减排也被国家社会所重视，实现可持续的绿色发展也是我国的重要目标。同时，随着生活水平的提高，越来越的商场和写字楼等大型建筑使用中央空调。在我国大型商用总耗能中中央空调约占40％-70％，2018年建筑建造和运行占全社会总能耗的36％。因此在建筑运行耗能方面，空调能耗占比是较大的，要做到节能减排，实现绿色发展，空调的节能减排是重中之重。
3.因此使用传感器技术、通信技术和先进的控制算法等进行空调运行控制的优化策略研究，来降低能耗，一直是国内外学者研究的重点。建筑系统内部较为复杂，不同建筑的能耗受到非常多因素的影响，几乎不可能实现最优控制。同时在空调用电期间，一直以来都是依赖管理员的操作来实现空调稳定的能源供给，而不是自动调节。然而目前除了稳定的能源供应外，消费者还要求节约能源和成本，再加之考虑到随季节和时间变化的能量需求以及相应的能耗成本，操作管理者很难很好的操作设备。
4.那么，在提倡节能减排的大环境和消费者想要降低成本的需求的条件下，需要一个可以给操作管理者提供能耗信息的咨询系统或设备。该咨询系统的主要功能是准确预测能源需求，来作为运行规划的基本条件，并能从节约能源、节约成本和保证能源供给稳定等角度，根据预测的能源需求适当的给出系统的运行规划。


技术实现要素：

5.本发明的目的是克服现有技术中存在的中央空调系统能耗的问题，提供了一种降低中央空调系统能耗的基于中央空调系统动态仿真平台的智能优化控制方法。
6.为实现以上目的，本发明的技术解决方案是：
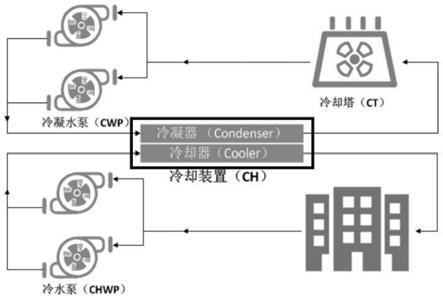
7.一种基于中央空调系统动态仿真平台的智能优化控制方法，所述控制方法基于中央空调系统，所述中央空调系统包括：冷却装置、冷却塔、冷凝水泵和冷却水泵，冷却装置通过相应管系连接至冷却塔，再连接至冷凝水泵，最后回到冷却装置；冷却水泵产生冷水通过冷却管系传输至冷却装置传入所需要降温的建筑；
8.所述智能优化控制方法包括如下步骤：
9.s1、数据预处理：
10.数据采集，首先从中央空调的控制系统中导出所有的运行数据资料文本；将导出的运行数据资料文本导入到matlab中，采用删除或采用均值插补法补全数据文本中的缺失值，采用皮尔逊积矩相关系数进行计算，其关系系数r的表达式为：
[0011][0012]
上式中，是参数x的平均值，是参数y的平均值；
[0013]
将文本中所有类别参数的数据资料两两分别带入式1进行计算得到各参数之间的相关性的绝对值；并分析数据之间的关联性得出关联性结论，此时进入下一步s2；
[0014]
s2、构建中央空调系统模型：
[0015]
根据s1中处理后的数据，选取与能耗数据关联性高的数据建立模型；首先，利用matlab建立冷却负载模型，然后通过分别建立冷却装置能耗模型，冷却塔风扇能耗模型，冷凝水泵能耗模型和冷却水泵能耗模型，最后建立整个中央空调系统的能耗模型，通过系统冷却负载模型和整个系统的能耗模型，得出系统的效率模型；
[0016]
s3、中央空调系统优化模型的建立：
[0017]
根据优化目标、各参数的约束关系和设备之间的关系，建立优化模型；中央空调系统的总能耗是四个主要装置能耗的和，不同设备的某个参数增大或减小，也会带来系统能耗的改变，通过这些参数的约束关系，建立中央空调系统的整体优化模型，再利用整体优化模型，对中央空调系统的运行进行优化。
[0018]
所述s1、数据预处理：
[0019]
数据采集，首先从中央空调的控制系统中导出所有的运行数据资料文本；
[0020]
将导出的运行数据资料文本导入到matlab中，采用删除或采用均值插补法补全数据文本中的缺失值，采用皮尔逊积矩相关系数进行计算，其关系系数r的表达式为：
[0021][0022]
上式中，是参数x的平均值，是参数y的平均值；
[0023]
将文本中所有类别参数的数据资料两两分别带入式1进行计算得到各参数之间的相关性的绝对值；下表以部分关系为例进行相关性分析，得出结果如下表1所示：
[0024]
表1参数之间的相关性
[0025][0026]
上表中的systotpower是指整个中央空调系统的能耗，chwp_pc为冷却水泵转速，cwp_pc为冷凝水泵转速，ct_pc为冷却塔风扇转速，cwrhdr流出冷凝装置水温，cwshdr为流入冷凝装置水温；由上表1得出结论：能耗量与冷却塔风扇转速、流出冷凝装置水温、流入冷
凝装置水温高度相关，此时进入下一步s2；
[0027]
所述s2、根据预处理结果构建中央空调系统模型：
[0028]
根据s1中处理后的数据，建立模型；首先，利用matlab建立冷却负载模型，然后通过分别建立冷却装置能耗模型，冷却塔风扇能耗模型，冷凝水泵能耗模型和冷却水泵能耗模型，最后建立整个中央空调系统的能耗模型，通过系统冷却负载模型和整个系统的能耗模型，得出系统的效率模型；
[0029]
s2.1、冷却负载数学模型的建立：冷却负载由冷却装置冷凝器和冷却器产生，冷却负载能耗与冷却负载与流入流出冷却装置的温差和水流速度有关，冷却负载能耗与水温差和水流速度成正比；冷却器的冷却负载q
e_chw
和冷凝器的冷却负载q
e_cw
分别为：
[0030]qe_chw
＝k1×mchwsfhdr
×
(t
chwrhd
r-t
chwshdr
)
ꢀꢀꢀꢀꢀ
(2)
[0031]qe_cw
＝k2×mcwsfhdr
×
(t
cwrhdr-t
cwshdr
)
ꢀꢀꢀꢀ
(3)
[0032]
上式中：m
chwsfhdr
为冷却器的水流速度，t
chwrhdr
为流入冷却器的水温，t
chwshdr
为流出冷却器的水温，k1冷却器的系数；m
cwsfhdr
为冷凝器的水流速度，t
cwrhdr
为流入冷凝器的水温，t
cwshdr
为流出冷凝器的水温，k2冷凝器的系数；中央空调系统冷却负载qe为冷却器负载和冷凝器负载之和，中央空调系统冷却负载qe为：
[0033]
qe＝α1q
e_chw
+α2q
e_cw
+α3ꢀꢀ
(4)
[0034]
上式中：qe为中央空调系统冷却负载，q
e_chw
为冷却器的冷却负载，q
e_cw
为冷凝器的冷却负载，α1、α2、α3为冷却负载回归系数；
[0035]
根据s1中的数据利用matlab对公式4进行线性拟合，得到：α1＝0.0746，α2＝0.0003，α3＝0.0339；得出中央空调系统的冷却负载模型：
[0036]
qe＝0.0746q
e_chw
+0.0003q
e_cw
+0.0339
ꢀꢀꢀ
(5)
[0037]
上式中：qe为中央空调系统的负载功率，q
e_chw
为冷却器的冷却负载，q
e_cw
为冷凝器的冷却负载；
[0038]
s2.2、冷却装置能耗数学模型的建立：冷却装置包括冷却器和冷凝器，是中央空调系统耗能最大的设备，它的能耗主要与经过冷却装置前后的水温和实际的冷却负载有关，可以得到得到冷却装置功率p
ch
的函数：
[0039]
p
ch
＝f(qe，δt
condenser
，δt
cooler
)
ꢀꢀꢀꢀ
(6)
[0040]
上式中：p
ch
为冷却装置功率，qe为冷却装置的制冷量即冷却负载，δt
conderser
为冷凝器温差δt
condennser
＝t
cwrhdr-t
cwshdr
，t
cwrhdr
为流入冷凝器的水温，t
cwshdr
为流出冷凝器的水温，δt
cooler
为冷却器温差δt
cooler
＝t
chwrhdr-t
chwshdr
，t
chwrhdr
为流入冷却器的水温，t
chwshdr
为流出冷却器的水温；
[0041]
对于多台冷却装置，冷却装置的开启台数越多冷却温差越大，即冷却效果越好，温差与台数正相关，所以多台冷却装置一起运行时的总能耗模型为：
[0042]
p
ch_total
＝α
’0+α
‘1(t
cwshdr-t
chwshdr
)+α
’2(t
cwshdr-t
chwshdr
)2+α
‘3qe+α
’4q
e2
ꢀꢀ
(7)
[0043]
上式中：p
ch
为冷却装置功率，t
cwrhdr
为流入冷凝器的水温，t
cwshdr
为流出冷凝器的水温，t
chwrhdr
为流入冷却器的水温，t
chwshdr
为流出冷却器的水温，qe为中央空调系统冷却负载，α
‘0、α
’1、α
‘2、α
’3、α
‘4冷却装置的为回归系数；根据s1中的数据利用matlab对公式8进行线性拟合，得到：α
‘0＝57.1523，α
’1＝-5.8677，α
‘2＝0.1636，α
’3＝-0.0015，α
‘4＝0.0000；得出多台冷却装置的总能耗模型p
ch
为：
[0044]
p
ch
＝
[0045]
57.1523-5.8677(t
cwshdr-t
chwshdr
)+0.16361(t
cwshdr-t
chwshdr
)
2-0.0015qeꢀꢀ
(8)
[0046]
s2.3、冷却塔能耗数学模型的建立：
[0047]
冷却塔是中央空调系统的散热设备；由冷却塔散热特性可知，影响冷却塔的主要因素是流入冷却塔的冷却水和流出冷却塔冷却水的温度差、冷却水的流量、湿球温度和空气流量；湿球温度是指通过蒸发水分所能达到的最低温度也叫热饱和温度，由传感器测量得出；空气流量可以通过改变冷却塔风扇转速来调节，风扇转速越快，空气流量越大，与此同时冷却塔输出功率也就越大；根据流入冷却塔的冷却水和流出冷却塔冷却水的温度差、冷却水的流量、冷却塔风扇转速和冷却塔功率；四种数据呈正相关，利用数值拟合的方式，可得冷却塔功率的模型为：
[0048]
p
ct
＝f(m
cwrhdr
，δt
condenser
，n
ct
)
ꢀꢀ
(9)
[0049]
进行拟合得到：
[0050]
p
ct
＝β1m
cwrhdr
+β2δt
condenser
+β3n
ct
+β4ꢀꢀ
(10)
[0051]
上式中：p
ct
为冷却塔功率，m
cwrhdr
为流入冷却塔的水流速度，即流出冷凝器的水流速度，n
ct
为冷却塔的转速，δt
conderser
表示的应该是冷凝器的水温差，β1、β2、β3、β4为冷却塔功率的回归系数；根据s1中的数据利用matlab对公式8进行线性拟合，得到：β1＝-0.8162，β2＝1.4932，β3＝0.8394，β4＝3.9335；因此冷却塔功率模型为：
[0052]
p
ct
＝-0.8162m
cwrhdr
+1.4932δt
condenser
+0.8394n
ct
+3.9335
ꢀꢀ
(11)
[0053]
s2.4、冷凝水泵能耗数学模型的建立：
[0054]
冷凝水泵的转速可以调节，频率在30hz-50hz之间，冷凝水泵的转速改变会使冷却水的流量、温度发生变化，因此冷凝水泵的能耗与转速、流量有关，而流量与冷凝水泵转速和开启台数有关，所以冷凝水泵的模型函数为：
[0055]
p
cwp
＝f(m
cwsfhdr
)
ꢀꢀ
(12)
[0056]mcwsfhdr
＝f(n
cwp
，n3)
ꢀꢀ
(13)
[0057]
上式中：p
cwp
为冷凝水泵功率，m
cwsfhdr
为冷凝水泵的水流速度，n
cwp
为冷凝水泵的转速，n3为冷凝水泵所打开的台数，n3≤3；使用matlab将冷凝水泵台数与冷凝水泵转速和水流速度进行线性拟合，得到冷凝水泵台数的模型为：
[0058]
n3＝1.852+0.001302m
cwsfhdr-0.53818n
cwp
ꢀꢀ
(14)
[0059]
上式中：m
cwsfhdr
为冷凝水泵的水流速度，n
cwp
为冷凝水泵的转速，n3为冷凝水泵所打开的台数；再根据冷凝水泵的功率，水流速度相关数据使用matlab对公式13进行线性拟合，得到冷凝水泵的能耗模型为：
[0060]
p
cwp
＝0.00751m
cwsfhdr-1.169
ꢀꢀ
(15)
[0061]
上式中：p
cwp
为冷凝水泵功率，m
cwsfhdr
为冷凝水泵的水流速度；
[0062]
s2.5、冷却水泵能耗数学模型的建立：
[0063]
冷却水泵的转速可以调节，频率在30hz-50hz之间，冷却水泵的转速改变会使冷却水的流量温度发生变化，因此冷却水泵的能耗与转速、流量有关，而流量与冷却水泵转速和开启台数有关，所以冷却水泵的模型为：
[0064]
p
chwp
＝f(m
chwsfhdr
)
ꢀꢀꢀꢀ
(16)
[0065]mchwsfhdr
＝f(n
chwp
，n2)
ꢀꢀꢀꢀꢀ
(17)
[0066]
上式中：p
chwp
为冷却水泵功率，n
chwp
为冷却水泵的转速，m
chwsfhdr
为冷凝水泵的水流速度，n2为冷却水泵所打开的台数，n2≤4；
[0067]
先根据数据将冷却水泵台数与冷却水泵转速和水流速度进行拟合，使用matlab对公式18进行线性拟合，得到冷却水泵台数拟合模型为：
[0068]
n2＝1.133+0.002394m
chwsfhdr-0.04235n
chwp
ꢀꢀ
(18)
[0069]
上式中：n
chwp
为冷却水泵转速，m
chwsfhdr
为冷凝水泵的水流速度，n4为冷却水泵所打开的台数，n4≤4；
[0070]
再根据冷却水泵功率和转速相关数据使用matlab对公式17进行线性拟合，得到冷却水泵的能耗模型为：
[0071]
p
chwp
＝0.0138m
chwsfhdr-4.432
ꢀꢀꢀꢀ
(19)
[0072]
s2.6、中央空调系统能耗和效率数学模型的建立：
[0073]
将上述能耗模型相加即可得到中央空调系统的能耗模型为：
[0074]
p
total
＝p
ch
+p
cwp
+p
chwp
+p
ct
ꢀꢀ
(20)
[0075]
上式中：p
total
为中央空调系统的总功率，p
ch
为冷却装置功率，p
cwp
为冷凝水泵功率，p
chwp
为冷却水泵功率，p
ct
为冷却塔功率；中央空调系统效率η为：
[0076]
η＝p
total
/qeꢀꢀ
(21)
[0077]
上式中：qe为中央空调系统的负载功率，p
total
为中央空调系统的总功率；
[0078]
此时中央空调系统的总能耗、总功率模型构建完成，进入下一步s3。
[0079]
所述s3、中央空调系统优化模型的建立：
[0080]
根据优化目标、各参数的约束关系和设备之间的关系，建立优化模型；中央空调系统的总能耗是四个主要装置能耗的和，不同设备的某个参数增大或减小，也会带来系统能耗的改变，通过这些参数的约束关系，建立优化模型；
[0081]
s3.1、设立优化目标：
[0082]
中央空调系统的设备状态最优控制策略的目标是使系统总能耗最低，同时系统效率最高，也要在满足冷却负载和环境的需求的前提下，其数学模型为：
[0083][0084]
上式中：冷却装置所打开的台数n1＝1，2，3；冷却水泵所打开的台数n2＝1，2，3，4；冷凝水泵所打开的台数n3＝1，2，3；冷却塔所打开的台数n4＝1，2；p
total
为中央空调系统的总能耗，zi为设备开启状态，zi＝0或1，0为未开启、1为已开启，p
ch
为冷却装置功率，p
cwp
为冷凝水泵功率，p
chwp
为冷却水泵功率，p
ct
为冷却塔功率；
[0085]
s3.2、设定约束条件：中央空调系统冷却负载约束：冷却负载必须满足需求约束：
[0086]
qe≥q
ꢀꢀ
(23)
[0087]
上式中：qe为中央空调系统冷却负载，q为所需求的冷却负载；
[0088]
中央空调系统的转速约束：冷却塔风扇转速n
ct
、冷却水泵转速n
chwp
、冷凝水泵转速n
cwp
都要在规定的范围内，因此约束为：
[0089]
[0090]
中央空调系统的温度约束：冷却水温不能太大也不能太小，因为需要与环境进行热交换，所以要高于环境的湿球温度，因此模型为：
[0091][0092]
上式中：t
chwshdr
为冷却水供水温，也是流出冷却器的水温，t
cwrhdr
为冷冻水供水温，也是流出冷凝器的水的温度，带有min为该水温的设定的最小值，带有max为该水温的设定的最大值；中央空调系统各设备之间的相互约束：冷却负载由冷却装置产生，即冷却水流入流出冷却装置后温度降低，冷却装置吸收热量产生冷却负载，所以得到冷却负载与冷却水的约束关系：
[0093]
qe＝c
·mchwsfhdr
·
(t
chwrhdr-t
chwshdr
)
ꢀꢀ
(26)
[0094]
上式中：qe为中央空调系统冷却负载，c为水的比热容，m
chwsfhdr
为冷却器的水流速度，即冷却水的流速，(t
chwrhdr-t
chwshdr
)为流入流出冷却器的水的温差，t
chwrhdr
为流入冷却器的水温，t
chwshdr
为流出冷却器的水温；
[0095]
冷却水带走了冷却装置的所有热量，因此约束关系为：
[0096]
p
ch
+qe＝c
·mchwsfhdr
·
(t
cwrhdr-t
cwshdr
)
ꢀꢀꢀꢀ
(27)
[0097]
上式中：p
ch
为冷却装置功率，qe为中央空调系统冷却负载，m
chwsfhdr
为冷凝器的水流速度，即冷却水的流速，(t
cwrhdr-t
cwshdr
)为流入流出冷凝器的水的温差，t
cwrhdr
为流入冷凝器的水温，t
cwshdr
为流出冷凝器的水温；冷却水泵与冷却塔之间的约束关系为：
[0098][0099]
上式中：p
ch
为冷却装置功率，qe为中央空调系统冷却负载，m
cwrhdr
为流入冷却塔的水流速度，即流出冷凝器的水流速度，n
ct
为冷却塔的转速，γ1、γ2、γ3均为比例系数；
[0100]
s3.3、建立优化模型：根据优化目标和约束条件相结合得到，整体优化模型如下：
[0101][0102]
(n1＝1，2，3；n2＝1，2，3，4；n3＝1，2，3；n4＝1，2)
[0103][0104]
此时优化模型构建完成。
[0105]
所述智能优化控制方法还包括s4、遗传算法应用求解及分析：
[0106]
对完成建模的中央空调的系统模型和优化模型利用遗传算法进行计算，设置初始
值群体规模n
p
，交叉概率pc，变异概率pm，终止进化代数g，然后进行遗传算法计算，最终得出最优的控制策略，将计算结果与原数据比较几个不同时间点的能耗和效率，验证中央空调的系统模型和优化模型的优化效果。
[0107]
与现有技术相比，本发明的有益效果为：
[0108]
1、本发明一种基于中央空调系统动态仿真平台的智能优化控制方法在建模过程中先针对系统的四个核心耗能装置进行数学建模，再将其相加得到总能耗模型，然后根据总能耗模型和冷却负载的关系得出效率模型。根据各约束，建立以最小能耗为目标的系统节能模型，最后利用遗传算法的出转速最优控制策略。根据对结果分析表明，本方法可以降低中央空调系统6％左右的能耗，提高中央空调系统5％左右的效率。因此，本方法能够为中央空调系统提供更加合理的智能优化控制方法，降低中央空调系统的能耗，提高系统效率。
[0109]
2、本发明一种基于中央空调系统动态仿真平台的智能优化控制方法中首先确认中央空调系统中各数据之间的关联性，然后选取关联性强的数据分别构建冷却装置、冷却塔、冷凝水泵和冷却水泵的能耗数学模型，然后将这四个数学模型求和得到中央空调总能耗的数学模型和系统的效率模型，本方法基于中央空调的实际运行数据然后利用matlab建模，模型的更加贴合实际情况，可靠性、精准度更高。因此，本设计是数学模型更加贴合实际情况，精准度更高。
[0110]
3、本发明一种基于中央空调系统动态仿真平台的智能优化控制方法中系统的总能耗是四个主要装置能耗的和，不同设备的某个参数增大或减小，也会带来系统能耗的改变，通过这些参数的约束关系，建立优化模型利用温度与转速进行一系列约束，得到精准的约束关系和优化目标。因此，本设计约束关系精准，优化目标明确。
[0111]
4、本发明一种基于中央空调系统动态仿真平台的智能优化控制方法中采用遗传算法进行仿真得出最优的控制方法，验证了建立模型的可行性，有效降低了耗电量提高了能量利用率。因此，本设计能够实现节能减排，提高能量利用率。
附图说明
[0112]
图1是本发明央空调系统的的结构示意图。
[0113]
图2是冷却负载模型残差图。
[0114]
图3是冷却温差和冷却装置开启台数关系图。
[0115]
图4是冷却装置能耗模型残差图。
[0116]
图5是冷却塔水温差、水流量、风扇转速和功率的关系图。
[0117]
图6是冷却塔功率模型残差图。
[0118]
图7是凝水泵台数拟合结果。
[0119]
图8是冷水泵台数拟合结果。
[0120]
图9是遗传算法流程图。
具体实施方式
[0121]
以下结合附图说明和具体实施方式对本发明作进一步详细的说明。
[0122]
参见图1至图9，一种基于中央空调系统动态仿真平台的智能优化控制方法，所述控制方法基于中央空调系统，所述中央空调系统包括：冷却装置、冷却塔、冷凝水泵和冷却
水泵，冷却装置通过相应管系连接至冷却塔，再连接至冷凝水泵，最后回到冷却装置；冷却水泵产生冷水通过冷却管系传输至冷却装置传入所需要降温的建筑；
[0123]
所述智能优化控制方法包括如下步骤：
[0124]
s1、数据预处理：
[0125]
数据采集，首先从中央空调的控制系统中导出所有的运行数据资料文本；
[0126]
将导出的运行数据资料文本导入到matlab中，采用删除或采用均值插补法补全数据文本中的缺失值，采用皮尔逊积矩相关系数进行计算，其关系系数r的表达式为：
[0127][0128]
上式中，是参数x的平均值，是参数y的平均值；
[0129]
将文本中所有类别参数的数据资料两两分别带入式1进行计算得到各参数之间的相关性的绝对值；并分析数据之间的关联性得出关联性结论，此时进入下一步s2；
[0130]
s2、构建中央空调系统模型：
[0131]
根据s1中处理后的数据，选取与能耗数据关联性高的数据建立模型；首先，利用matlab建立冷却负载模型，然后通过分别建立冷却装置能耗模型，冷却塔风扇能耗模型，冷凝水泵能耗模型和冷却水泵能耗模型，最后建立整个中央空调系统的能耗模型，通过系统冷却负载模型和整个系统的能耗模型，得出系统的效率模型；
[0132]
s3、中央空调系统优化模型的建立：
[0133]
根据优化目标、各参数的约束关系和设备之间的关系，建立优化模型；中央空调系统的总能耗是四个主要装置能耗的和，不同设备的某个参数增大或减小，也会带来系统能耗的改变，通过这些参数的约束关系，建立中央空调系统的整体优化模型，再利用整体优化模型，对中央空调系统的运行进行优化。
[0134]
所述s1、数据预处理：
[0135]
数据采集，首先从中央空调的控制系统中导出所有的运行数据资料文本；
[0136]
将导出的运行数据资料文本导入到matlab中，采用删除或采用均值插补法补全数据文本中的缺失值，采用皮尔逊积矩相关系数进行计算，其关系系数r的表达式为：
[0137][0138]
上式中，是参数x的平均值，是参数y的平均值；
[0139]
将文本中所有类别参数的数据资料两两分别带入式1进行计算得到各参数之间的相关性的绝对值；下表以部分关系为例进行相关性分析，得出结果如下表1所示：
[0140]
表1参数之间的相关性
[0141][0142]
上表中的systotpower是指整个中央空调系统的能耗，chwp_pc为冷却水泵转速，cwp_pc为冷凝水泵转速，ct_pc为冷却塔风扇转速，cwrhdr流出冷凝装置水温，cwshdr为流入冷凝装置水温；由上表1得出结论：能耗量与冷却塔风扇转速、流出冷凝装置水温、流入冷凝装置水温高度相关，此时进入下一步s2；
[0143]
所述s2、根据预处理结果构建中央空调系统模型：
[0144]
根据s1中处理后的数据，建立模型；首先，利用matlab建立冷却负载模型，然后通过分别建立冷却装置能耗模型，冷却塔风扇能耗模型，冷凝水泵能耗模型和冷却水泵能耗模型，最后建立整个中央空调系统的能耗模型，通过系统冷却负载模型和整个系统的能耗模型，得出系统的效率模型；
[0145]
s2.1、冷却负载数学模型的建立：冷却负载由冷却装置冷凝器和冷却器产生，冷却负载能耗与冷却负载与流入流出冷却装置的温差和水流速度有关，冷却负载能耗与水温差和水流速度成正比；冷却器的冷却负载q
e_chw
和冷凝器的冷却负载q
e_cw
分别为：
[0146]qe_chw
＝k1×mchwsfhdr
×
(t
chwrhd
r-t
chwshdr
)
ꢀꢀꢀꢀꢀꢀꢀꢀ
(2)
[0147]qe_cw
＝k2×mcwsfhdr
×
(t
cwrhdr-t
cwshdr
)
ꢀꢀꢀꢀꢀꢀ
(3)
[0148]
上式中：m
chwsfhdr
为冷却器的水流速度，t
chwrhdr
为流入冷却器的水温，t
chwshdr
为流出冷却器的水温，k1冷却器的系数；m
cwsfhdr
为冷凝器的水流速度，t
cwrhdr
为流入冷凝器的水温，t
cwshdr
为流出冷凝器的水温，k2冷凝器的系数；中央空调系统冷却负载qe为冷却器负载和冷凝器负载之和，中央空调系统冷却负载qe为：
[0149]
qe＝α1q
e_chw
+α2q
e_cw
+α3ꢀꢀ
(4)
[0150]
上式中：qe为中央空调系统冷却负载，q
e_chw
为冷却器的冷却负载，q
e_cw
为冷凝器的冷却负载，α1、α2、α3为冷却负载回归系数；
[0151]
根据s1中的数据利用matlab对公式4进行线性拟合，得到：α1＝0.0746，α2＝0.0003，α3＝0.0339；得出中央空调系统的冷却负载模型：
[0152]
qe＝0.0746q
e_chw
+0.0003q
e_cw
+0.0339
ꢀꢀꢀꢀ
(5)
[0153]
上式中：qe为中央空调系统的负载功率，q
e_chw
为冷却器的冷却负载，q
e_cw
为冷凝器的冷却负载；
[0154]
s2.2、冷却装置能耗数学模型的建立：冷却装置包括冷却器和冷凝器，是中央空调系统耗能最大的设备，它的能耗主要与经过冷却装置前后的水温和实际的冷却负载有关，可以得到得到冷却装置功率p
ch
的函数：
[0155]
p
ch
＝f(qe，δt
condenser
，δt
cooler
)
ꢀꢀꢀꢀ
(6)
[0156]
上式中：p
ch
为冷却装置功率，qe为冷却装置的制冷量即冷却负载，δt
conderser
为冷凝器温差δt
condenser
＝t
cwrhdr-t
cwshdr
，t
cwrhdr
为流入冷凝器的水温，t
cwshdr
为流出冷凝器的水温，δt
cooler
为冷却器温差δt
cooler
＝t
chwrhdr-t
chwshdr
，t
chwrhdr
为流入冷却器的水温，t
chwshdr
为流出冷却器的水温；
[0157]
对于多台冷却装置，冷却装置的开启台数越多冷却温差越大，即冷却效果越好，温差与台数正相关，所以多台冷却装置一起运行时的总能耗模型为：
[0158]
p
ch_total
＝α
’0+α
‘1(t
cwshdr-t
chwshdr
)+α
’2(t
cwshdr-t
chwshdr
)2+α
‘3qe+α
’4q
e2
ꢀꢀ
(7)
[0159]
上式中：p
ch
为冷却装置功率，t
cwrhdr
为流入冷凝器的水温，t
cwshdr
为流出冷凝器的水温，t
chwrhdr
为流入冷却器的水温，t
chwshdr
为流出冷却器的水温，qe为中央空调系统冷却负载，α
‘0、α
’1、α
‘2、α
’3、α
‘4冷却装置的为回归系数；根据s1中的数据利用matlab对公式8进行线性拟合，得到：α
‘0＝57.1523，α
’1＝-5.8677，α
‘2＝0.1636，α
′3＝-0.0015，α
‘4＝0.0000；得出多台冷却装置的总能耗模型p
ch
为：
[0160]
p
ch
＝
[0161]
57.1523-5.8677(t
cwshdr-t
chwshdr
)+0.16361(t
cwshdr-t
chwshdr
)
2-0.0015qeꢀꢀ
(8)
[0162]
s2.3、冷却塔能耗数学模型的建立：
[0163]
冷却塔是中央空调系统的散热设备；由冷却塔散热特性可知，影响冷却塔的主要因素是流入冷却塔的冷却水和流出冷却塔冷却水的温度差、冷却水的流量、湿球温度和空气流量；湿球温度是指通过蒸发水分所能达到的最低温度也叫热饱和温度，由传感器测量得出；空气流量可以通过改变冷却塔风扇转速来调节，风扇转速越快，空气流量越大，与此同时冷却塔输出功率也就越大；根据流入冷却塔的冷却水和流出冷却塔冷却水的温度差、冷却水的流量、冷却塔风扇转速和冷却塔功率；四种数据呈正相关，利用数值拟合的方式，可得冷却塔功率的模型为：
[0164]
p
ct
＝f(m
cwrhdr
，δt
condenser
，n
ct
)
ꢀꢀ
(9)
[0165]
进行拟合得到：
[0166]
p
ct
＝β1m
cwrhdr
+β2δt
condenser
+β3n
ct
+β4ꢀꢀ
(10)
[0167]
上式中：p
ct
为冷却塔功率，m
cwrhdr
为流入冷却塔的水流速度，即流出冷凝器的水流速度，n
ct
为冷却塔的转速，δt
conderser
表示的应该是冷凝器的水温差，β1、β2、β3、β4为冷却塔功率的回归系数；根据s1中的数据利用matlab对公式8进行线性拟合，得到：β1＝-0.8162，β2＝1.4932，β3＝0.8394，β4＝3.9335；因此冷却塔功率模型为：
[0168]
p
ct
＝-0.8162m
cwrhdr
+1.4932δt
condenser
+0.8394n
ct
+3.9335
ꢀꢀ
(11)
[0169]
s2.4、冷凝水泵能耗数学模型的建立：
[0170]
冷凝水泵的转速可以调节，频率在30hz-50hz之间，冷凝水泵的转速改变会使冷却水的流量、温度发生变化，因此冷凝水泵的能耗与转速、流量有关，而流量与冷凝水泵转速和开启台数有关，所以冷凝水泵的模型函数为：
[0171]
p
cwp
＝f(m
cwsfhdr
)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(12)
[0172]mcwsfhdr
＝f(n
cwp
，n3)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(13)
[0173]
上式中：p
cwp
为冷凝水泵功率，m
cwsfhdr
为冷凝水泵的水流速度，n
cwp
为冷凝水泵的转速，n3为冷凝水泵所打开的台数，n3≤3；使用matlab将冷凝水泵台数与冷凝水泵转速和水流速度进行线性拟合，得到冷凝水泵台数的模型为：
[0174]
n3＝1.852+0.001302m
cwsfhdr-0.53818n
cwp
ꢀꢀꢀꢀ
(14)
[0175]
上式中：m
cwsfhdr
为冷凝水泵的水流速度，n
cwp
为冷凝水泵的转速，n3为冷凝水泵所打开的台数；再根据冷凝水泵的功率，水流速度相关数据使用matlab对公式13进行线性拟合，得到冷凝水泵的能耗模型为：
[0176]
p
cwp
＝0.00751m
cwsfhdr-1.169
ꢀꢀ
(15)
[0177]
上式中：p
cwp
为冷凝水泵功率，m
cwsfhdr
为冷凝水泵的水流速度；
[0178]
s2.5、冷却水泵能耗数学模型的建立：
[0179]
冷却水泵的转速可以调节，频率在30hz-50hz之间，冷却水泵的转速改变会使冷却水的流量温度发生变化，因此冷却水泵的能耗与转速、流量有关，而流量与冷却水泵转速和开启台数有关，所以冷却水泵的模型为：
[0180]
p
chwp
＝f(m
chwsfhdr
)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(16)
[0181]mchwsfhdr
＝f(n
chwp
，n2)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(17)
[0182]
上式中：p
chwp
为冷却水泵功率，n
chwp
为冷却水泵的转速，m
chwsfhdr
为冷凝水泵的水流速度，n2为冷却水泵所打开的台数，n2≤4；
[0183]
先根据数据将冷却水泵台数与冷却水泵转速和水流速度进行拟合，使用matlab对公式18进行线性拟合，得到冷却水泵台数拟合模型为：
[0184]
n2＝1.133+0.002394m
chwsfhdr-0.04235n
chwp
ꢀꢀ
(18)
[0185]
上式中：n
chwp
为冷却水泵转速，m
chwsfhdr
为冷凝水泵的水流速度，n4为冷却水泵所打开的台数，n4≤4；
[0186]
再根据冷却水泵功率和转速相关数据使用matlab对公式17进行线性拟合，得到冷却水泵的能耗模型为：
[0187]
p
chwp
＝0.0138m
chwsfhdr-4.432
ꢀꢀꢀꢀ
(19)
[0188]
s2.6、中央空调系统能耗和效率数学模型的建立：
[0189]
将上述能耗模型相加即可得到中央空调系统的能耗模型为：
[0190]
p
total
＝p
ch
+p
cwp
+p
chwp
+p
ct
ꢀꢀ
(20)
[0191]
上式中：p
total
为中央空调系统的总功率，p
ch
为冷却装置功率，p
cwp
为冷凝水泵功率，p
chwp
为冷却水泵功率，p
ct
为冷却塔功率；中央空调系统效率η为：
[0192]
η＝p
total
/qeꢀꢀ
(21)
[0193]
上式中：qe为中央空调系统的负载功率，p
total
为中央空调系统的总功率；
[0194]
此时中央空调系统的总能耗、总功率模型构建完成，进入下一步s3。
[0195]
所述s3、中央空调系统优化模型的建立：
[0196]
根据优化目标、各参数的约束关系和设备之间的关系，建立优化模型；中央空调系统的总能耗是四个主要装置能耗的和，不同设备的某个参数增大或减小，也会带来系统能耗的改变，通过这些参数的约束关系，建立优化模型；
[0197]
s3.1、设立优化目标：
[0198]
中央空调系统的设备状态最优控制策略的目标是使系统总能耗最低，同时系统效率最高，也要在满足冷却负载和环境的需求的前提下，其数学模型为：
[0199][0200]
上式中：冷却装置所打开的台数n1＝1，2，3；冷却水泵所打开的台数n2＝1，2，3，4；
冷凝水泵所打开的台数n3＝1，2，3；冷却塔所打开的台数n4＝1，2；p
total
为中央空调系统的总能耗，zi为设备开启状态，zi＝0或1，0为未开启、1为已开启，p
ch
为冷却装置功率，p
cwp
为冷凝水泵功率，p
chwp
为冷却水泵功率，p
ct
为冷却塔功率；
[0201]
s3.2、设定约束条件：中央空调系统冷却负载约束：冷却负载必须满足需求约束：
[0202]
qe≥q
ꢀꢀ
(23)
[0203]
上式中：qe为中央空调系统冷却负载，q为所需求的冷却负载；
[0204]
中央空调系统的转速约束：冷却塔风扇转速n
ct
、冷却水泵转速n
chwp
、冷凝水泵转速n
cwp
都要在规定的范围内，因此约束为：
[0205][0206]
中央空调系统的温度约束：冷却水温不能太大也不能太小，因为需要与环境进行热交换，所以要高于环境的湿球温度，因此模型为：
[0207][0208]
上式中：t
chwshdr
为冷却水供水温，也是流出冷却器的水温，t
cwrhdr
为冷冻水供水温，也是流出冷凝器的水的温度，带有min为该水温的设定的最小值，带有max为该水温的设定的最大值；中央空调系统各设备之间的相互约束：冷却负载由冷却装置产生，即冷却水流入流出冷却装置后温度降低，冷却装置吸收热量产生冷却负载，所以得到冷却负载与冷却水的约束关系：
[0209]
qe＝c
·mchwsfhdr
·
(t
chwrhdr-t
chwshdr
)
ꢀꢀꢀꢀ
(26)
[0210]
上式中：qe为中央空调系统冷却负载，c为水的比热容，m
chwsfhdr
为冷却器的水流速度，即冷却水的流速，(t
chwrhdr-t
chwshdr
)为流入流出冷却器的水的温差，t
chwrhdr
为流入冷却器的水温，t
chwshdr
为流出冷却器的水温；
[0211]
冷却水带走了冷却装置的所有热量，因此约束关系为：
[0212]
p
ch
+qe＝c
·mchwsfhdr
·
(t
cwrhdr-t
cwshdr
)
ꢀꢀꢀ
(27)
[0213]
上式中：p
ch
为冷却装置功率，qe为中央空调系统冷却负载，m
chwsfhdr
为冷凝器的水流速度，即冷却水的流速，(t
cwrhdr-t
cwshdr
)为流入流出冷凝器的水的温差，t
cwrhdr
为流入冷凝器的水温，t
cwshdr
为流出冷凝器的水温；冷却水泵与冷却塔之间的约束关系为：
[0214][0215]
上式中：p
ch
为冷却装置功率，qe为中央空调系统冷却负载，m
cwrhdr
为流入冷却塔的水流速度，即流出冷凝器的水流速度，n
ct
为冷却塔的转速，γ1、γ2、γ3均为比例系数；
[0216]
s3.3、建立优化模型：根据优化目标和约束条件相结合得到，整体优化模型如下：
[0217][0218]
(n1＝1，2，3；n2＝1，2，3，4；n3＝1，2，3；n4＝1，2)
[0219][0220]
此时优化模型构建完成。
[0221]
所述智能优化控制方法还包括s4、遗传算法应用求解及分析：
[0222]
对完成建模的中央空调的系统模型和优化模型利用遗传算法进行计算，设置初始值群体规模n
p
，交叉概率pc，变异概率pm，终止进化代数g，然后进行遗传算法计算，最终得出最优的控制策略，将计算结果与原数据比较几个不同时间点的能耗和效率，验证中央空调的系统模型和优化模型的优化效果。
[0223]
本发明的原理说明如下：
[0224]
(1)创建初始种群。将进化代数设为零，然后设置最大可进化代数，随机生成初始群体其中包含数个随机生成的个体。(2)个体评价。计算每个体的适应度根据事先设置好的适应度函数来。(3)选择运算。选择适应度高的个体遗传到下一代，选择作用于群体。(4)交叉运算。以某一概率交换上一步选择出的适应度高的个体的染色体，产生新的个体，此运算也是作用于群体。(5)变异运算。以某一概率选择个体，再将该个体的某个或某些基因值以某一概率改变为某个等位基因。(6)循环操作。计算经过上述步骤产生的新的群体的各个个体的适应度，将个体按适应度高低进行排序，准备执行下一次遗传操作。(7)停止条件判断。若迭代次数小于等于设置的最大进化代数，未遗传算法继续进行，转到步骤(2)；若迭代次数大于设置的最大进化代数，则达到停止条件，此次进化过程中所得到的具有最大适应度的个体作为最优解输出，本次遗传算法结束。
[0225]
实施例1：
[0226]
一种基于中央空调系统动态仿真平台的智能优化控制方法，所述控制方法基于中央空调系统，所述中央空调系统包括：冷却装置、冷却塔、冷凝水泵和冷却水泵，冷却装置通过相应管系连接至冷却塔，再连接至冷凝水泵，最后回到冷却装置；冷却水泵产生冷水通过冷却管系传输至冷却装置传入所需要降温的建筑；
[0227]
所述智能优化控制方法包括如下步骤：
[0228]
s1、数据预处理：
[0229]
数据采集，首先从中央空调的控制系统中导出所有的运行数据资料文本；
[0230]
将导出的运行数据资料文本导入到matlab中，采用删除或采用均值插补法补全数据文本中的缺失值，采用皮尔逊积矩相关系数进行计算，其关系系数r的表达式为：
[0231][0232]
上式中，是参数x的平均值，是参数y的平均值；
[0233]
将文本中所有类别参数的数据资料两两分别带入式1进行计算得到各参数之间的相关性的绝对值；并分析数据之间的关联性得出关联性结论，此时进入下一步s2；
[0234]
s2、构建中央空调系统模型：
[0235]
根据s1中处理后的数据，选取与能耗数据关联性高的数据建立模型；首先，利用matlab建立冷却负载模型，然后通过分别建立冷却装置能耗模型，冷却塔风扇能耗模型，冷凝水泵能耗模型和冷却水泵能耗模型，最后建立整个中央空调系统的能耗模型，通过系统冷却负载模型和整个系统的能耗模型，得出系统的效率模型；
[0236]
s3、中央空调系统优化模型的建立：
[0237]
根据优化目标、各参数的约束关系和设备之间的关系，建立优化模型；中央空调系统的总能耗是四个主要装置能耗的和，不同设备的某个参数增大或减小，也会带来系统能耗的改变，通过这些参数的约束关系，建立中央空调系统的整体优化模型，再利用整体优化模型，对中央空调系统的运行进行优化。
[0238]
实施例2：
[0239]
实施例2与实施例1基本相同，其不同之处在于：
[0240]
所述s1、数据预处理：
[0241]
数据采集，首先从中央空调的控制系统中导出所有的运行数据资料文本；
[0242]
将导出的运行数据资料文本导入到matlab中，采用删除或采用均值插补法补全数据文本中的缺失值，采用皮尔逊积矩相关系数进行计算，其关系系数r的表达式为：
[0243][0244]
上式中，是参数x的平均值，是参数y的平均值；
[0245]
将文本中所有类别参数的数据资料两两分别带入式1进行计算得到各参数之间的相关性的绝对值；下表以部分关系为例进行相关性分析，得出结果如下表1所示：
[0246]
表1参数之间的相关性
[0247]
[0248]
上表中的systotpower是指整个中央空调系统的能耗，chwp_pc为冷却水泵转速，cwp_pc为冷凝水泵转速，ct_pc为冷却塔风扇转速，cwrhdr流出冷凝装置水温，cwshdr为流入冷凝装置水温；由上表1得出结论：能耗量与冷却塔风扇转速、流出冷凝装置水温、流入冷凝装置水温高度相关，此时进入下一步s2；
[0249]
所述s2、根据预处理结果构建中央空调系统模型：
[0250]
根据s1中处理后的数据，建立模型；首先，利用matlab建立冷却负载模型，然后通过分别建立冷却装置能耗模型，冷却塔风扇能耗模型，冷凝水泵能耗模型和冷却水泵能耗模型，最后建立整个中央空调系统的能耗模型，通过系统冷却负载模型和整个系统的能耗模型，得出系统的效率模型；
[0251]
s2.1、冷却负载数学模型的建立：冷却负载由冷却装置冷凝器和冷却器产生，冷却负载能耗与冷却负载与流入流出冷却装置的温差和水流速度有关，冷却负载能耗与水温差和水流速度成正比；冷却器的冷却负载q
e_chw
和冷凝器的冷却负载q
e_cw
分别为：
[0252]qe_chw
＝k1×mchwsfhdr
×
(t
chwrhdr-t
chwshdr
)
ꢀꢀꢀꢀꢀꢀ
(2)
[0253]qe_cw
＝k2×mcwsfhdr
×
(t
cwrhdr-t
cwshdr
)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(3)
[0254]
上式中：m
chwsfhdr
为冷却器的水流速度，t
chwrhdr
为流入冷却器的水温，t
chwshdr
为流出冷却器的水温，k1冷却器的系数；m
cwsfhdr
为冷凝器的水流速度，t
cwrhdr
为流入冷凝器的水温，t
cwshdr
为流出冷凝器的水温，k2冷凝器的系数；中央空调系统冷却负载qe为冷却器负载和冷凝器负载之和，中央空调系统冷却负载qe为：
[0255]
qe＝α1q
e_chw
+α2q
e_cw
+α3ꢀꢀ
(4)
[0256]
上式中：qe为中央空调系统冷却负载，q
e_chw
为冷却器的冷却负载，q
e_cw
为冷凝器的冷却负载，α1、α2、α3为冷却负载回归系数；
[0257]
根据s1中的数据利用matlab对公式4进行线性拟合，得到：α1＝0.0746，α2＝0.0003，α3＝0.0339；得出中央空调系统的冷却负载模型：
[0258]
qe＝0.0746q
e_chw
+0.0003q
e_cw
+0.0339
ꢀꢀꢀꢀ
(5)
[0259]
上式中：qe为中央空调系统的负载功率，q
e_chw
为冷却器的冷却负载，q
e_cw
为冷凝器的冷却负载；
[0260]
s2.2、冷却装置能耗数学模型的建立：冷却装置包括冷却器和冷凝器，是中央空调系统耗能最大的设备，它的能耗主要与经过冷却装置前后的水温和实际的冷却负载有关，可以得到得到冷却装置功率p
ch
的函数：
[0261]
p
ch
＝f(qe，δt
condenser
，δt
cooler
)
ꢀꢀꢀꢀ
(6)
[0262]
上式中：p
ch
为冷却装置功率，qe为冷却装置的制冷量即冷却负载，δt
conderser
为冷凝器温差δt
condennser
＝t
cwrhdr-t
cwshdr
，t
cwrhdr
为流入冷凝器的水温，t
cwshdr
为流出冷凝器的水温，δt
cooler
为冷却器温差δt
cooler
＝t
chwrhdr-t
chwshdr
，t
chwrhdr
为流入冷却器的水温，t
chwshdr
为流出冷却器的水温；
[0263]
对于多台冷却装置，冷却装置的开启台数越多冷却温差越大，即冷却效果越好，温差与台数正相关，所以多台冷却装置一起运行时的总能耗模型为：
[0264]
p
ch_total
＝α
’0+α
‘1(t
cwshdr-t
chwshdr
)+α
’2(t
cwshdr-t
chwshd
r)2+α
‘3qe+α
’4q
e2
ꢀꢀ
(7)
[0265]
上式中：p
ch
为冷却装置功率，t
cwrhdr
为流入冷凝器的水温，t
cwshdr
为流出冷凝器的水温，t
chwrhdr
为流入冷却器的水温，t
chwshdr
为流出冷却器的水温，qe为中央空调系统冷却负载，
α
‘0、α
’1、α
‘2、α
’3、α
‘4冷却装置的为回归系数；根据s1中的数据利用matlab对公式8进行线性拟合，得到：α
‘0＝57.1523，α
’1＝-5.8677，α
‘2＝0.1636，α
’3＝-0.0015，α
‘4＝0.0000；得出多台冷却装置的总能耗模型p
ch
为：
[0266]
p
ch
＝
[0267]
57.1523-5.8677(t
cwshdr-t
chwshdr
)+0.16361(t
cwshdr-t
chwshdr
)
2-0.0015qeꢀꢀ
(8)
[0268]
s2.3、冷却塔能耗数学模型的建立：
[0269]
冷却塔是中央空调系统的散热设备；由冷却塔散热特性可知，影响冷却塔的主要因素是流入冷却塔的冷却水和流出冷却塔冷却水的温度差、冷却水的流量、湿球温度和空气流量；湿球温度是指通过蒸发水分所能达到的最低温度也叫热饱和温度，由传感器测量得出；空气流量可以通过改变冷却塔风扇转速来调节，风扇转速越快，空气流量越大，与此同时冷却塔输出功率也就越大；根据流入冷却塔的冷却水和流出冷却塔冷却水的温度差、冷却水的流量、冷却塔风扇转速和冷却塔功率；四种数据呈正相关，利用数值拟合的方式，可得冷却塔功率的模型为：
[0270]
p
ct
＝f(m
cwrhdr
，δt
condenser
，n
ct
)
ꢀꢀ
(9)
[0271]
进行拟合得到：
[0272]
p
ct
＝β1m
cwrhdr
+β2δt
condenser
+β3n
ct
+β4ꢀꢀ
(10)
[0273]
上式中：p
ct
为冷却塔功率，m
cwrhdr
为流入冷却塔的水流速度，即流出冷凝器的水流速度，n
ct
为冷却塔的转速，δt
conderser
表示的应该是冷凝器的水温差，β1、β2、β3、β4为冷却塔功率的回归系数；根据s1中的数据利用matlab对公式8进行线性拟合，得到：β1＝-0.8162，β2＝1.4932，β3＝0.8394，β4＝3.9335；因此冷却塔功率模型为：
[0274]
p
ct
＝-0.8162m
cwrhdr
+1.4932δt
condenser
+0.8394n
ct
+3.9335
ꢀꢀ
(11)
[0275]
s2.4、冷凝水泵能耗数学模型的建立：
[0276]
冷凝水泵的转速可以调节，频率在30hz-50hz之间，冷凝水泵的转速改变会使冷却水的流量、温度发生变化，因此冷凝水泵的能耗与转速、流量有关，而流量与冷凝水泵转速和开启台数有关，所以冷凝水泵的模型函数为：
[0277]
p
cwp
＝f(m
cwsfhdr
)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(12)
[0278]mcwsfhdr
＝f(n
cwp
，n3)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(13)
[0279]
上式中：p
cwp
为冷凝水泵功率，m
cwsfhdr
为冷凝水泵的水流速度，n
cwp
为冷凝水泵的转速，n3为冷凝水泵所打开的台数，n3≤3；使用matlab将冷凝水泵台数与冷凝水泵转速和水流速度进行线性拟合，得到冷凝水泵台数的模型为：
[0280]
n3＝1.852+0.001302m
cwsfhdr-0.53818n
cwp
ꢀꢀꢀꢀ
(14)
[0281]
上式中：m
cwsfhdr
为冷凝水泵的水流速度，n
cwp
为冷凝水泵的转速，n3为冷凝水泵所打开的台数；再根据冷凝水泵的功率，水流速度相关数据使用matlab对公式13进行线性拟合，得到冷凝水泵的能耗模型为：
[0282]
p
cwp
＝0.00751m
cwsfhdr-1.169
ꢀꢀꢀꢀ
(15)
[0283]
上式中：p
cwp
为冷凝水泵功率，m
cwsfhdr
为冷凝水泵的水流速度；
[0284]
s2.5、冷却水泵能耗数学模型的建立：
[0285]
冷却水泵的转速可以调节，频率在30hz-50hz之间，冷却水泵的转速改变会使冷却水的流量温度发生变化，因此冷却水泵的能耗与转速、流量有关，而流量与冷却水泵转速和
开启台数有关，所以冷却水泵的模型为：
[0286]
p
chwp
＝f(m
chwsfhdr
)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(16)
[0287]mchwsfhdr
＝f(n
chwp
，n2)
ꢀꢀꢀꢀꢀꢀꢀꢀ
(17)
[0288]
上式中：p
chwp
为冷却水泵功率，n
chwp
为冷却水泵的转速，m
chwsfhdr
为冷凝水泵的水流速度，n2为冷却水泵所打开的台数，n2≤4；
[0289]
先根据数据将冷却水泵台数与冷却水泵转速和水流速度进行拟合，使用matlab对公式18进行线性拟合，得到冷却水泵台数拟合模型为：
[0290]
n2＝1.133+0.002394m
chwsfhdr-0.04235n
chwp
ꢀꢀꢀꢀꢀ
(18)
[0291]
上式中：n
chwp
为冷却水泵转速，m
chwsfhdr
为冷凝水泵的水流速度，n4为冷却水泵所打开的台数，n4≤4；
[0292]
再根据冷却水泵功率和转速相关数据使用matlab对公式17进行线性拟合，得到冷却水泵的能耗模型为：
[0293]
p
chwp
＝0.0138m
chwsfhdr-4.432
ꢀꢀꢀꢀ
(19)
[0294]
s2.6、中央空调系统能耗和效率数学模型的建立：
[0295]
将上述能耗模型相加即可得到中央空调系统的能耗模型为：
[0296]
p
total
＝p
ch
+p
cwp
+p
chwp
+p
ct
ꢀꢀ
(20)
[0297]
上式中：p
total
为中央空调系统的总功率，p
ch
为冷却装置功率，p
cwp
为冷凝水泵功率，p
chwp
为冷却水泵功率，p
ct
为冷却塔功率；中央空调系统效率η为：
[0298]
η＝p
total
/qeꢀꢀ
(21)
[0299]
上式中：qe为中央空调系统的负载功率，p
total
为中央空调系统的总功率；
[0300]
此时中央空调系统的总能耗、总功率模型构建完成，进入下一步s3。
[0301]
所述s3、中央空调系统优化模型的建立：
[0302]
根据优化目标、各参数的约束关系和设备之间的关系，建立优化模型；中央空调系统的总能耗是四个主要装置能耗的和，不同设备的某个参数增大或减小，也会带来系统能耗的改变，通过这些参数的约束关系，建立优化模型；
[0303]
s3.1、设立优化目标：
[0304]
中央空调系统的设备状态最优控制策略的目标是使系统总能耗最低，同时系统效率最高，也要在满足冷却负载和环境的需求的前提下，其数学模型为：
[0305][0306]
上式中：冷却装置所打开的台数n1＝1，2，3；冷却水泵所打开的台数n2＝1，2，3，4；冷凝水泵所打开的台数n3＝1，2，3；冷却塔所打开的台数n4＝1，2；p
total
为中央空调系统的总能耗，zi为设备开启状态，zi＝0或1，0为未开启、1为已开启，p
ch
为冷却装置功率，p
cwp
为冷凝水泵功率，p
chwp
为冷却水泵功率，p
ct
为冷却塔功率；
[0307]
s3.2、设定约束条件：中央空调系统冷却负载约束：冷却负载必须满足需求约束：
[0308]
qe≥q
ꢀꢀ
(23)
[0309]
上式中：qe为中央空调系统冷却负载，q为所需求的冷却负载；
[0310]
中央空调系统的转速约束：冷却塔风扇转速n
ct
、冷却水泵转速n
chwp
、冷凝水泵转速n
cwp
都要在规定的范围内，因此约束为：
[0311][0312]
中央空调系统的温度约束：冷却水温不能太大也不能太小，因为需要与环境进行热交换，所以要高于环境的湿球温度，因此模型为：
[0313][0314]
上式中：t
chwshdr
为冷却水供水温，也是流出冷却器的水温，t
cwrhdr
为冷冻水供水温，也是流出冷凝器的水的温度，带有min为该水温的设定的最小值，带有max为该水温的设定的最大值；中央空调系统各设备之间的相互约束：冷却负载由冷却装置产生，即冷却水流入流出冷却装置后温度降低，冷却装置吸收热量产生冷却负载，所以得到冷却负载与冷却水的约束关系：
[0315]
qe＝c
·mchwsfhdr
·
(t
chwrhdr-t
chwshdr
)
ꢀꢀꢀꢀ
(26)
[0316]
上式中：qe为中央空调系统冷却负载，c为水的比热容，m
chwsfhdr
为冷却器的水流速度，即冷却水的流速，(t
chwrhdr-t
chwshdr
)为流入流出冷却器的水的温差，t
chwrhdr
为流入冷却器的水温，t
chwshdr
为流出冷却器的水温；
[0317]
冷却水带走了冷却装置的所有热量，因此约束关系为：
[0318]
p
ch
+qe＝c
·mchwsfhdr
·
(t
cwrhdr-t
cwshdr
)
ꢀꢀꢀꢀ
(27)
[0319]
上式中：p
ch
为冷却装置功率，qe为中央空调系统冷却负载，m
chwsfhdr
为冷凝器的水流速度，即冷却水的流速，(t
cwrhdr-t
cwshdr
)为流入流出冷凝器的水的温差，t
cwrhdr
为流入冷凝器的水温，t
cwshdr
为流出冷凝器的水温；冷却水泵与冷却塔之间的约束关系为：
[0320][0321]
上式中：p
ch
为冷却装置功率，qe为中央空调系统冷却负载，m
cwrhdr
为流入冷却塔的水流速度，即流出冷凝器的水流速度，n
ct
为冷却塔的转速，γ1、γ2、γ3均为比例系数；
[0322]
s3.3、建立优化模型：根据优化目标和约束条件相结合得到，整体优化模型如下：
[0323][0324]
(n1＝1，2，3；n2＝1，2，3，4；n3＝1，2，3；n4＝1，2)
[0325][0326]
此时优化模型构建完成。
[0327]
实施例3：
[0328]
实施例3与实施例2基本相同，其不同之处在于：
[0329]
所述智能优化控制方法还包括s4、遗传算法应用求解及分析：
[0330]
对完成建模的中央空调的系统模型和优化模型利用遗传算法进行计算，设置初始值群体规模n
p
，交叉概率pc，变异概率pm，终止进化代数g，然后进行遗传算法计算，最终得出最优的控制策略，将计算结果与原数据比较几个不同时间点的能耗和效率，验证中央空调的系统模型和优化模型的优化效果。
[0331]
要实现中央空调系统总耗电最低，途径主要是控制几个耗能机构总体的能耗最低，将控制几个能耗机构的转速来实现，算法实现如图2，所示因此染色体上的基因片段为冷却水泵转速、冷凝水泵转速和冷却塔风扇转速，这三个转速范围分别是30hz-50hz、30hz-50hz和25hz-50hz，为了方便表达将三个转速百分化，即现在的转速范围为0-100％(以冷水塔风扇转速举例为0时候转速为25hz，40％时转速为35hz，100％时转速为50hz)；此时范围所需要的转速控制的二进制编码转换为十进制需要大于100因此合适的二进制为7位，用[1，1，1，0，0，0，0]来表示基因片段；之后加入条件使其在一百以内，因为七位的二进制编码等于128大于100；染色体由这三个基因片段构成，可以表示为[1，1，1，0，0，0，0，1，1，1，0，1，0，0，1，1，1，0，0，1，0]，此时即为一个个体；
[0332]
之后进行初始种群设置，对种群的大小进行设置，同时也对染色体上的基因片段进行赋值，设置适应度函数，即上一节的系统总耗电模型。本次算法计算时，初始值的设置为，群体规模n
p
＝50，交叉概率pc＝0.6，变异概率pm＝0.01，终止进化代数g＝250。
[0333]
本次算法计算时，初始值的设置为，群体规模n
p
＝50，交叉概率pc＝0.6，变异概率pm＝0.01，终止进化代数g＝250。经过计算后，将得到的结果与原数据比较几个不同时间点的能耗和效率，得到最优控制策略如表2所示，部分原数据如表3所示。
[0334]
表2最优控制策略
[0335][0336]
上式中：三个转速为百分比，实际具体计算方式前文以给出。
[0337]
表3部分原数据
[0338][0339][0340]
以上是随机选取的部分数据进行对比，优化策略还是相当有作用，系统总耗电比原数据降低，系统效率相比得到提升。