一种基于多激励函数极限学习机的自适应污水处理控制方法与流程

1.本发明涉及控制科学与工程、环境科学与工程领域，尤其涉及一种基于多激励函数极限学习机的自适应污水处理控制方法。


背景技术：

2.水是生命之源，是人类发展不可或缺的战略资源。而由于人类的污染浪费及水资源自身所具有的特性导致水资源在部分地区相当短缺，同时收到污染的水不仅会进一步污染自然界的水源，破坏环境，威胁动植物的生存家园，同时也会反作用于人类，压缩人类生存空间，并威胁人类健康安全，所以对污水进行处理是一项必不可少的工业环节。通过将受到污染的水进行处理达标以后再排放或再利用，则可以避免对环境与人类社会造成破坏，同时也可以缓解由于人类社会过度发展导致的水资源短缺问题。
3.受限于材料设计以及成本约束，目前世界上大部分的污水处理都采用厌氧好氧的生化反应来实现对于污水的处理，通过微生物的厌氧好氧生化反应，将污水中主要的有机物都降解为无机盐，并通过沉淀的形式去除，沉淀之后的清水则通过沉淀池上方排出，达标后进入江河湖泊，或者企业内部循环使用，或者用于城市绿化等，沉淀的污泥则通过干燥等手段形成淤泥，并无害化处理。该方法具有成本少，易于建造大型污水处理厂等优势，但同时，反应过程相当复杂，且是一个长延时、大扰动、强耦合的系统，所以往往受到各种内外因素的影响，使得污水出水水质不达标，为了实现对于污水处理的有效控制，各种方法被广泛提出。很多方法都是基于数学模型进行的控制，但是由于污水处理系统的复杂性，难以构建精确的模型，很难从机理建模的角度对污水处理系统进行控制方法分析与研究。


技术实现要素：

4.为了确保出水水质的达标，且同时考虑到污水处理系统的复杂性以及模型的未知性，本发明提出一种基于多激励函数极限学习机的自适应污水处理控制方法，实现对于污水处理出水水质中的溶解氧浓度进行控制，因为溶解氧浓度作为一种关键组分能够有效的反映出水水质是否达标，从而实现对于水质达标的保证。
5.本发明提出的基于多激励函数极限学习机的自适应污水处理控制方法，主要是针对污水处理过程中的溶解氧浓度进行有效控制，其中被控变量为溶解氧浓度s
o
，而操作变量则为氧气传递系数k
l
a，目标是将溶解氧浓度控制在设定值附近，控制方法具体包括有数据预处理、神经网络初始化、神经网络在线迭代以及构成基于多激励函数极限学习机的控制器设计，从而实现对于污水处理出水溶解氧浓度实现设定值控制。主要步骤如下所示：
6.(1)数据预处理
7.对控制器的输入输出数据x进行归一化，x＝[s
o
,k
l
a]，s
o
为溶解氧浓度，即被控变量， k
l
a为氧气传递系数，即操作变量，将不同量纲的数据归一化至[
‑
1,1]之间，得到归一化后的样本数据x。
[0008]
(2)构建基于极限学习机的控制器
[0009]
首先，将被控污水处理系统描述为：
[0010]
y
k+1
＝f(x
k
)+g(x
k
)u
k
+δ
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(1)
[0011]
其中y
k+1
是下一时刻的系统输出，即表征下一时刻溶解氧浓度s
o
(t+1)，x
k
为当前系统状态，即表征当前时刻溶解氧浓度s
o
(t)，u
k
为控制信号，表征氧气传递系数k
l
a(t)；f(
·
)为系统动态函数，g(
·
)为系统输出增益函数，f(
·
)与g(
·
)均为未知函数，δ为系统未知扰动。
[0012]
其次，利用神经网络来估计被控污水处理系统，公式如下：
[0013][0014]
其中与分别为f(
·
)与g(
·
)的估计函数，δ
f
为系统的重构误差。
[0015]
(3)利用多种激励函数的模式来实现对参数的学习，选择p种激励函数，分别用基于每一种激励函数的极限学习机估计f(
·
)与g(
·
)，则有：
[0016][0017][0018]
其中与分别为基于第j种激励函数对f(
·
)与g(
·
)的估计函数，与分别表示神经网络与的第i个隐含层到输出层的权重，l为神经网络隐含层节点个数，g
j
(
·
,
·
,
·
)为隐含层的输出，a
ij
与b
ij
分别为第j种隐含层激励函数的第i组设定参数。
[0019]
将极限学习机神经网络带入公式(2)则有：
[0020][0021]
其中h
jk
＝[g
j
(a
1j
,b
1j
,x
k
),...,g
j
(a
lj
,b
lj
,x
k
),g
j
(a
(l+1)j
,b
(l+1)j
,x
k
)u
k
,...,g
j
(a
2lj
,b
2lj
,x
k
)u
k
]，δ
jf
为第j 次估计的重构误差，为隐含层到输出层的初始权重矩阵。
[0022]
污水处理的估计模型如下所示：
[0023][0024]
其中为下一时刻估计输出，为第j种激励函数的第k时刻隐含层到输出层的估计权重。
[0025]
(4)计算当前的系统输出误差：
[0026][0027]
其中为系统输出真实值与基于第j种激励函数估计值之间的误差，为基于第j 种激励函数的神经网络估计值，种激励函数的神经网络估计值，与分别为与的估计值。
[0028]
(5)更新神经网络隐含层到输出层的权重矩阵：
[0029][0030]
其中p
j(k
‑
1)
与p
jk
分别为第j种激励函数的第k+1时刻与第k时刻的中间参数，中间参数初始值
[0031]
(6)返回步骤(3)，累加j值，重复操作步骤，直至j＝p。
[0032]
(7)计算当前控制器输出：
[0033][0034]
其中y
d
为被控污水处理系统的设定输出。
[0035]
将当前控制信号u
k
输入被控系统，实现对当前被控系统的控制，当系统在下一时刻产生新的数据时，令j＝1，返回步骤(3)，直至污水处理系统停止工作。
[0036]
进一步地，所述步骤(1)中，采用最大最小值归一化法，将不同量纲的数据归一化至[
‑
1,1] 之间，从而消除量纲对控制器的控制性能带来的影响，具体表达形式为：
[0037][0038]
其中x为原样本数据，x
min
为样本数据中的最小值，x
max
为样本数据中的最大值，x为归一化后的样本数据。
[0039]
本发明的有益效果如下：本发明控制方法不需要依赖被控污水处理系统的机理模型，直接利用系统的输入输出数据对控制器进行动态调整，避免因为被控污水处理系统过于复杂对控制器设计所带来的阻碍，同时采用多激励函数进行估计系统动态的方法，使得控制方法具有较强的鲁棒性与较好的控制性能。而采用极限学习机进行训练与控制，可以获得极其快速的学习速率，并且能够在极短的时间内完成计算，降低由于控制器计算所带来的系统延时，本发明方法在污水处理系统的实际应用方面具有一定的研究意义与进一步探索的价值。
附图说明
[0040]
图1为实施例中被控污水处理系统的示意图；
[0041]
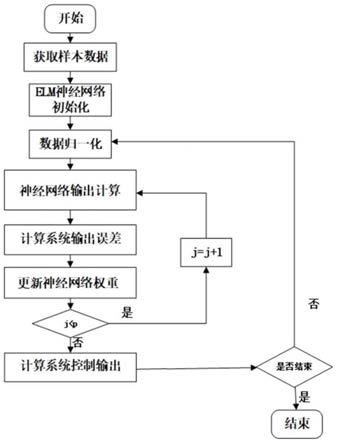
图2为本发明基于多激励函数极限学习机的自适应污水处理控制方法流程图；
[0042]
图3为溶解氧浓度控制效果图。
[0043]
具体实施方法
[0044]
为使本发明的目的、技术方案及优点更加清楚明白，以下结合附图及实施例对本发明进行进一步的详细说明。应当理解，此处所描述的具体实施方式仅仅用以解释本发明，并不限定本发明的保护范围。
[0045]
图1为被控污水处理系统的一个示例。本发明提出的基于多激励函数极限学习机的自适应污水处理控制方法，主要是针对污水处理过程中的溶解氧浓度进行有效控制，其
中被控变量为溶解氧浓度s
o
，而操作变量则为氧气传递系数k
l
a，目标是将溶解氧浓度控制在设定值附近，如图2所示，具体步骤如下：
[0046]
(1)数据预处理
[0047]
对控制器的输入输出数据进行归一化，具体采用最大最小值归一化算法，将不同量纲的数据归一化至[
‑
1,1]之间，从而消除量纲对控制器的控制性能带来的影响，具体表达形式为：
[0048][0049]
其中x为原样本数据，具体实际中为x＝[s
o
,k
l
a]，s
o
为溶解氧浓度，即被控变量，k
l
a 为氧气传递系数，即操作变量，也就是对控制器的输入输出均做归一化处理，x
min
为样本数据中的最小值，而x
max
则为样本数据中的最大值，x为归一化后的样本数据。
[0050]
(2)构建基于极限学习机的控制器
[0051]
首先，将被控污水处理系统描述为：
[0052]
y
k+1
＝f(x
k
)+g(x
k
)u
k
+δ
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(2)
[0053]
其中y
k+1
是下一时刻的系统输出，即表征下一时刻溶解氧浓度s
o
(t+1)，x
k
为当前系统状态，即表征当前时刻溶解氧浓度s
o
(t)，u
k
为控制信号，表征氧气传递系数k
l
a(t)；f(
·
)为系统动态函数，g(
·
)为系统输出增益函数，考虑到污水处理系统的复杂特性，f(
·
)与g(
·
)均为未知函数，而δ为系统未知扰动。
[0054]
其次，利用神经网络来估计被控污水处理系统，公式如下：
[0055][0056]
其中与分别为f(
·
)与g(
·
)的估计函数，δ
f
为系统的重构误差。
[0057]
(3)考虑到在构建神经网络的时候，不同的激励函数对最终的估计结果具有较大的影响，所以为了消除由于激励函数对估计效果所产生的影响，本发明引入多种激励函数的模式来实现对参数的学习，选择p种激励函数，分别用基于每一种激励函数的极限学习机估计f(
·
)与g(
·
)，则有：
[0058][0059][0060]
其中与分别为基于第j种激励函数对f(
·
)与g(
·
)的估计函数，与分别表示神经网络与的第i个隐含层到输出层的权重，l为神经网络隐含层节点个数，而g
j
(
·
,
·
,
·
) 则为隐含层的输出，其中a
ij
与b
ij
分别为第j种隐含层激励函数的第i组设定参数。
[0061]
将极限学习机神经网络带入公式(3)则有：
[0062][0063]
其中h
jk
＝[g
j
(a
1j
,b
1j
,x
k
),...,g
j
(a
lj
,b
lj
,x
k
),g
j
(a
(l+1)j
,b
(l+1)j
,x
k
)u
k
,...,g
j
(a
2lj
,b
2lj
,x
k
)u
k
]，δ
jf
为第j 次估计的重构误差，可以看到，该方法利用一个神经网络同时对f(
·
)与g(
·
)进行估计。其中为隐含层到输出层的初始权重矩阵。则可以进一步得到污水处理的估计模型如下所示：
[0064][0065]
其中为下一时刻估计输出，而则为第j种激励函数的第k时刻隐含层到输出层的估计权重。
[0066]
(4)计算当前的系统输出误差：
[0067][0068]
其中为系统输出真实值与基于第j种激励函数估计值之间的误差，而则为基于第j种激励函数的神经网络估计值，其中则为基于第j种激励函数的神经网络估计值，其中与分别为与的估计值。
[0069]
(5)更新神经网络隐含层到输出层的权重矩阵：
[0070][0071]
其中p
j(k
‑
1)
与p
jk
分别为第j种激励函数的第k+1时刻与第k时刻的中间参数，中间参数初始值
[0072]
(6)返回步骤(3)，累加j值(即令j＝j+1)，重复操作步骤，直至j＝p。
[0073]
(7)计算当前控制器输出：
[0074][0075]
其中y
d
为被控污水处理系统的设定输出。
[0076]
将当前控制信号u
k
输入被控系统，实现对当前被控系统的控制，当系统在下一时刻产生新的数据时，令j＝1，返回步骤(3)，直至污水处理系统停止工作。
[0077]
图3为溶解氧浓度控制效果图，从图3可以看出，本发明提出的自适应污水处理控制方法相比较传统的pi控制方法具有更好的控制性能，可以有效提升污水处理系统的出水水质。
[0078]
以上所述仅是本发明的优选实施方式，虽然本发明已以较佳实施例披露如上，然而并非用以限定本发明。任何熟悉本领域的技术人员，在不脱离本发明技术方案范围情况下，都可利用上述揭示的方法和技术内容对本发明技术方案做出许多可能的变动和修饰，或修改为等同变化的等效实施例。因此，凡是未脱离本发明技术方案的内容，依据本发明的技术实质对以上实施例所做的任何的简单修改、等同变化及修饰，均仍属于本发明技术方
案保护的范围内。