一种风电机组风机轴承的健康状态评估方法与流程

本发明涉及风电设备状态评估的，尤其涉及到一种风电机组风机轴承的健康状态评估方法。

背景技术：

1、风电机组风机轴承是风电机组中的核心零部件之一，主要功能是支撑旋转轴或其他运动体，引导转动或移动运动，并承受由轴、轴上零件传递而来的载荷。因此，对风电机组风机轴承进行健康状态评估显得尤为重要。

2、现有的对风电机组风机轴承进行健康状态评估的方法包括：

3、传统方法：

4、主要通过观察轴承的磨损、裂纹以及表面质量等来评估健康状态，需要停机检修，并且结果依赖于检测人员的主观判断。

5、振动分析方法：

6、利用轴承的振动信号来评估健康状态，可实现在线监测，对磨损、裂纹等问题具有高度敏感性。常用的振动分析包括时域分析、频域分析和小波分析等。

7、上述两种方法均没有考虑风机轴承易受重载、高温等外部扰动的影响，因此，健康状态评估的结果并不准确。

技术实现思路

1、本发明的目的在于克服现有技术的不足，提供一种评估准确率高的风电机组风机轴承的健康状态评估方法。

2、为实现上述目的，本发明所提供的技术方案为：

3、一种风电机组风机轴承的健康状态评估方法，包括：

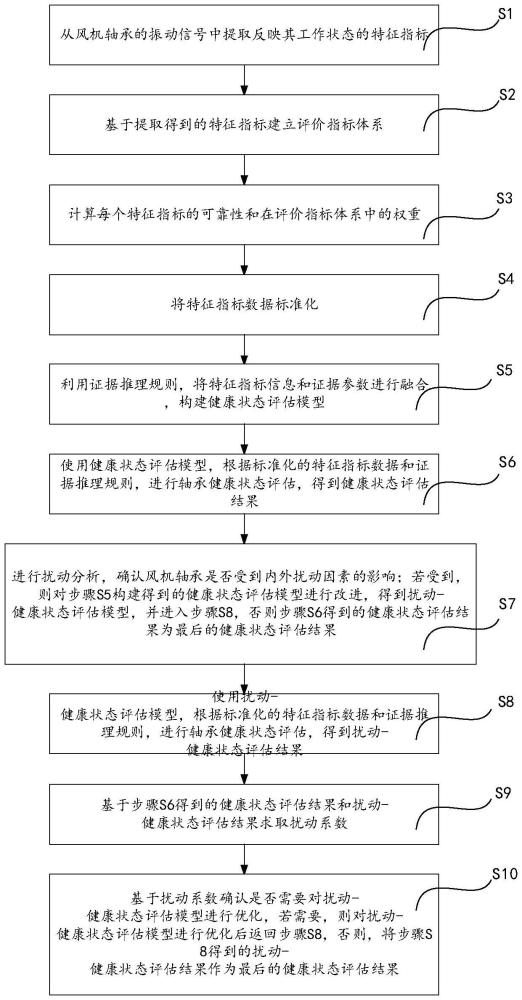
4、s1、从风机轴承的振动信号中提取反映其工作状态的特征指标；

5、s2、基于提取得到的特征指标建立评价指标体系；

6、s3、计算每个特征指标的可靠性和在评价指标体系中的权重；

7、s4、将特征指标数据标准化；

8、s5、利用证据推理规则，将特征指标信息和证据参数进行融合，构建健康状态评估模型；

9、s6、使用健康状态评估模型，根据标准化的特征指标数据和证据推理规则，进行轴承健康状态评估，得到健康状态评估结果；

10、s7、进行扰动分析，确认风机轴承是否受到内外扰动因素的影响；若受到，则对步骤s5构建得到的健康状态评估模型进行改进，得到扰动-健康状态评估模型，并进入步骤s8，否则步骤s6得到的健康状态评估结果为最后的健康状态评估结果；

11、s8、使用扰动-健康状态评估模型，根据标准化的特征指标数据和证据推理规则，进行轴承健康状态评估，得到扰动-健康状态评估结果；

12、s9、基于步骤s6得到的健康状态评估结果和扰动-健康状态评估结果求取扰动系数；

13、s10、基于扰动系数确认是否需要对扰动-健康状态评估模型进行优化，若需要，则对扰动-健康状态评估模型进行优化后返回步骤s8，否则，将步骤s8得到的扰动-健康状态评估结果作为最后的健康状态评估结果。

14、进一步地，提取的特征指标包括风机轴承磨损度对应值、反映风机轴承局部故障点受到的冲击力的峰值、峰值因子、反映风机轴承振动信号的波形指数的平均振幅、峰度、质心频率、均方根频率。

15、进一步地，风机轴承磨损度对应值rms的计算公式如下：

16、

17、y(i)为通过采样获得的离散时间振动信号，i＝1,2,3,...,ns，ns是振动信号的个数；

18、反映风机轴承局部故障点受到的冲击力的峰值yp的计算公式如下：

19、yp＝max(y(i)),i＝1,2,...,ns

20、峰值因子cf的计算公式如下：

21、

22、平均振幅sy的计算公式如下：

23、

24、为连续时间振动信号的平均值，其计算公式如下：

25、

26、峰度kurtosis{y(t)}的计算公式如下：

27、

28、质心频率cf的计算公式如下：：

29、

30、f1为频率域中的频率值，f2为通过傅里叶变换得到的信号的功率谱；功率谱p(f)为信号的傅里叶变换的模的平方：

31、

32、x(n)为离散信号序列，n为离散信号采样点，j为复数的虚数单位，ω为角频率；

33、均方根频率rmsf的计算公式如下：

34、

35、进一步地，风机轴承磨损度对应值rms的计算公式如下：

36、

37、y(i)为通过采样获得的离散时间振动信号，i＝1,2,3,...,ns，ns是振动信号的个数；反映风机轴承局部故障点受到的冲击力的峰值yp的计算公式如下：

38、yp＝max(y(i)),i＝1,2,...,ns

39、峰值因子cf的计算公式如下：

40、

41、平均振幅sy的计算公式如下：

42、

43、为连续时间振动信号的平均值，其计算公式如下：

44、

45、峰度kurtosis{y(t)}的计算公式如下：

46、

47、质心频率cf的计算公式如下：：

48、

49、f1为频率域中的频率值，f2为通过傅里叶变换得到的信号的功率谱；功率谱p(f)为信号的傅里叶变换的模的平方：

50、

51、x(n)为离散信号序列，n为离散信号采样点，j为复数的虚数单位，ω为角频率；

52、均方根频率rmsf的计算公式如下：

53、

54、进一步地，计算指标权重的过程包括：

55、设有指标n，并且指标的权重是ω1,ω2,...,ωn；

56、计算评价指标的标准差vi：

57、

58、为所有指标数据在时间k段内的平均值；然后，对变异系数进行归一化处理，并计算出评价指标的权重ωi：

59、

60、进一步地，将特征指标数据标准化包括：

61、先确定指标参考等级和参考值；然后，基于参考等级和参考值，采用基于规则的信息转换方法，将指标数据转换为信念分布的形式：

62、

63、其中，hi,j为指标i在第j个等级上的参考值；hi,j+1为指标i在第j+1个等级上的参考值；pi,j为指标i的输入值落在等级j上的概率；pi,j+1为指标i的输入值落在等级j+1上的概率；pi,k为指标i的输入值落在等级k上的概率；xi,j为指标i在第j个等级上的输入数据。

64、进一步地，使用健康状态评估模型，根据标准化的特征指标数据和证据推理规则，进行轴承健康状态评估，包括：

65、设一个节点收集数据片段t，并且每个信息片段都有指示器；输入的指标数据为xi，ei作为证据表示，i＝1,...,i，i为指标的数量；辨别的框架由n评价层次hn组成，n＝1,...,n，n为评价等级的总数，即θ＝{h1,...,hn}；经过数据标准化后，证据表示为以下信念分布形式：

66、ei＝{(hn,pn,i),n＝1,...,n；(θ,pθ,i)}

67、pn,i为指标i的标准化输入数据在评价等级hn下的信念程度；θ为包括所有评价水平的识别框架；pθ,i是指标相对于识别框架θ的信念程度；

68、证据的可靠性为ri，其满足0≤ri≤1；证据权重为ωi，经过归一化后即可满足0≤ωi≤1；具有可靠性的证据ei的加权信念分布为：

69、

70、p(θ)其中为功率集，为评价等级hn下指标i的混合概率质量，满足：

71、

72、

73、crw,i＝1/(1+ωi-ri)为正则化系数；mn,i为评价等级hn下指标i的基本概率质量，为空集，满足mn,i＝ωipn,i；

74、各指示器从不同的角度描述风机轴承振动信号的特性；各指标的数据进行标准化处理；对于任意两个证据ei，ej，评价它们的联合信念支持度pn,e(2)为：

75、

76、为ei和ej组合后分配给评价等级hn的非标准化组合概率质量；为ei和ej组合后分配给评价等级d的非标准化组合概率质量ei，ej；a，b均为评价等级hn的非空子集；

77、综合信念pn,e(i)由i个证据的公式确定:

78、

79、其中，k＝3,4,...,i，mn,e(k-1)，ma,e(k-1)为初始指标k-1组合后分配给等级hn和等级a的归一化组合概率质量；为第一个指标k融合后分配给功率集的未归一化概率质量，mp(θ),e(k-1)为第一个指标k-1融合后分配给功率集的归一化概率质量；分别为分配给评价等级hn和d的第一个k指标组合后的非归一化组合概率质量；pn,e(k)是融合后第一个指标k对评价等级hn的信念程度，且满足mn,e(1)＝mn,1，mp(θ),e(1)＝mp(θ),1；通过迭代，得到综合评价结果：

80、e(i)＝{(hn,pn,e(i)),n＝1,...,n,(θ,pθ,e(i))}

81、设评价等级hn的效用为u(hn)，得到评价结果的预期效用：

82、

83、u(e(i))为评价的预期效用，用于评价电机轴承的健康状态，即对应得到pm(xi)；pm(xi)为在输入指标数据xi下的健康状态评估结果，u(e(i))为综合考虑所有输入参数和证据后的综合效用的健康状态评估结果，该两者在结果上是等价的。

84、进一步地，使用扰动-健康状态评估模型，根据标准化的特征指标数据和证据推理规则，进行轴承健康状态评估时，评价模型的识别框架为θ＝{h1,...,hn}，证据分别为ei，i＝1,...,i，各证据区域对应的信度{r'1,r'2,...,r'i}和权重{ω'1,ω'2,...,ω'i}，参考值为hi,j，i＝1,2,...,i，j＝1,2,...,j，扰动条件下指标证据ei的信念分布计算如下：

85、

86、k≠l,l+1，hi和h1分别对应最大参考值和最小参考值，xi为输入指标数据，hl+1≤xi≤hl；σi为扰动强度，δxi为扰动变量；

87、采用基于规则的信息变换方法将其转换为信念分布形式，采用证据推理规则融合所有指标，得到轴承的扰动-健康状态评估结果，也即得到对应的输入指标数据xi下的扰动-健康状态评估结果pm(xi+σiδxi)。

88、进一步地，基于步骤s6得到的健康状态评估结果和扰动-健康状态评估结果求取扰动系数si，计算公式如下：

89、

90、pm(xi+σiδxi)为扰动-健康状态评估结果，pm(xi)为健康状态评估结果；xi为输入指标数据；σi为扰动强度，δxi为扰动变量。

91、进一步地，若扰动系数si≤|ε|，ε为扰动系数的最大误差，则不需要对扰动-健康状态评估模型进行优化，否则需要对扰动-健康状态评估模型进行优化。

92、与现有技术相比，本技术方案原理及优点如下：

93、本技术方案利用证据推理规则对多个特征指标进行融合决策，避免了单一指标评估的局限性，从而提高健康状态评估的准确度；进一步地，评估过程中考虑风机轴承易受重载、高温等外部扰动的影响，从而进一步提高健康状态评估的准确度。