一种基于阵列受限自组装有序微结构的制备方法与流程
本发明涉及软物质自组装领域,涉及如何调控纳米粒子/聚合物体系的自组装获得具有高度有序微结构的复合材料,具体为一种基于阵列受限自组装有序微结构的制备方法。
背景技术:
在聚合物中加入纳米粒子,两者在纳米尺度的复合将有可能获得不同于常规材料的纳米复合材料,从而在先进电子器件、光学器件、精密机械器件、航空航天器件、军事化学、生物医学及化学化工等领域发挥常规材料无法比拟的作用。
纳米粒子/聚合物体系的受限经历了从硬板受限到软板受限、从平板受限到柱状、球状受限的过程。其中的自组装研究都反映了利用外界影响探索有序微结构的可能性,因此寻找能有效调控微结构排列和取向的手段是一个值得深入研究的问题。
到目前为止,还没有发现纳米粒子/聚合物体系在阵列受限下自组装的有关报道。本发明提供一种阵列受限的方法,阵列受限打破了传统受限情况下受限界面的空间连续性,不可穿透的周期性排列的阵列柱体将在空间多个方向上直接调节聚合物链的伸展以及纳米粒子在空间的位置,从而控制最终平衡态的结构和取向。将阵列受限应用于纳米粒子/聚合物体系,可以得到结构新颖的高度有序的微结构,为开发新型纳米复合材料提供理论指导。
技术实现要素:
本发明的目的是为了提供一种基于阵列受限自组装有序微结构的制备方法,通过阵列受限的方法,对纳米粒子/聚合物体系进行受限,从而获得不同于传统受限方法的新颖而复杂的纳米微结构。
为了实现上述发明目的,本发明采用了以下技术方案:一种基于阵列受限自组装有序微结构的制备方法,包括以下步骤:步骤1.设计柱体阵列,具体包括以下步骤:步骤(1-1)确定柱体的形状,具体如下:所述柱体的横截面形状采用正方形、矩形、工字形、h形、圆形;步骤(1-2)确定柱体的排列方式,具体如下:所述柱体的排列方式采用四方排布、四方镶嵌排布和十字排布;步骤(1-3)确定柱体的表面性质,具体如下:柱体表面不可穿透,且与纳米粒子和聚合物既不排斥也不吸引;
步骤2.建立纳米粒子/聚合物体系受限在异形双柱体阵列中的自组装模型,具体包括以下步骤:(2-1)建立系统的自由能;(2-2)对自由能变分,得到一套自洽的方程组;(2-3)对自洽的方程组编程进行计算机模拟;
步骤3.通过程序反复调试,获得产生图案化结构的各种参数,具体如下:取聚合物单体的长度作为单位长度,具体参数取为:聚合物的聚合度n为100,纳米粒子为球形,半径为2,纳米粒子与聚合物的相互作用参数χn=28。系统尺寸为lx×ly×lz,z方向上柱体的高度lz取无限高,lx和ly根据柱体阵列确定;
步骤4.将纳米粒子的体积分数由低到高逐渐增加,从而实现微结构的调控;
步骤5.进一步调节系统和柱体的尺寸,以及纳米粒子与聚合物的体积比,获得其他的图案化结构;
步骤6.设计其他的柱体阵列,重复以上步骤1-步骤5,获得不同的有序微结构。
8.优选的,在步骤(2-1)中,系统的自由能(以kbt为能量单位)表示成如下形式:
其中,kb为玻耳兹曼常量,t为开氏温度,,
优选的,u(r)为设计柱体作用在纳米粒子/聚合物系统上的表面场,表示成如下形式:
相应地,总的体积分数φ0(r)为
优选的,在步骤(2-2)中,将自由能变分,得到如下形式的自洽方程组:
其中q(r,s)和q+(r,s)为聚合物的末端配分函数,可以用如下修正的扩散方程求解:
其中,初始条件为:q(r,0)=1和q+(r,1)=1,vr为纳米粒子的体积,等于
优选的,在步骤(2-3)中,将自洽方程组编程,自洽迭代,数值模拟求解,可得平衡态时纳米粒子和聚合物的体积分数
优选的,在步骤3中,最终参数取为:h形柱体的尺寸hx=48,hx=36,取柱体的各边分别为a、b、c、d、e、a’、b’、c’、d’、e’,其中柱体a、b、c和a’、b’、c’边的长度相等,各占hx的1/3;d、e和d’、e’边的长度相等,各占hy的1/3,相邻两个柱体中心之间的距离为dx=dy=64,系统尺寸lx=ly=256,在这个尺寸内分别包含四行四列的h形柱体阵列,利用周期性边界条件,x,y方向上的柱体可以向外周期性延伸。
优选的,当纳米粒子的体积分数比较小的时候,纳米粒子在聚合物中是均匀分布的,随着纳米粒子体积分数的增加,纳米粒子与聚合物发生了相分离,纳米粒子/聚合物混合体系的结构变得越来越复杂,自组装形成了有序的微结构,结构仍保持高度有序。
与现有技术相比,采用了上述技术方案的基于阵列受限自组装有序微结构的制备方法,具有如下有益效果:采用本发明的基于阵列受限自组装有序微结构的制备方法,将柱体阵列受限引入到纳米粒子/聚合物体系,获得不同于传统受限的高度有序的微结构,丰富了调控自组装结构的手段,并改变纳米粒子的体积分数,随着纳米粒子体积分数的增加,纳米粒子/聚合物混合体系的结构变得越来越复杂,同时结构仍然保持高度有序,利用柱体阵列可以很好地形成新颖而复杂的高度有序的微结构。
附图说明
图1为本发明基于阵列受限自组装有序微结构的制备方法实施例的结构示意图;
图2为本实施例中阵列受限下形成的部分图案化的结构示意图;
图3为本实施例中异形双柱体阵列的排布示意图。
具体实施方式
下面结合附图对本发明做进一步描述。
基于阵列受限自组装有序微结构的制备方法,包括以下步骤:步骤1.设计柱体阵列,具体包括以下步骤:步骤(1-1)确定柱体的形状,具体如下:柱体的横截面形状采用正方形、矩形、工字形、h形、圆形;步骤(1-2)确定柱体的排列方式,具体如下:所述柱体的排列方式采用四方排布、四方镶嵌排布和十字排布,如图3所示为柱体阵列的排布示意图,其中,(a)四方排列;(b)四方镶嵌排列;(c)十字排列;步骤(1-3)确定柱体的表面性质,具体如下:柱体表面不可穿透,且与纳米粒子和聚合物既不排斥也不吸引;
步骤2.建立纳米粒子/聚合物体系受限在异形双柱体阵列中的自组装模型,具体包括以下步骤:(2-1)建立系统的自由能,具体如下:系统的自由能(以kbt为能量单位)表示成如下形式:
其中,kb为玻耳兹曼常量,t为开氏温度,,
其中,u(r)为设计柱体作用在纳米粒子/聚合物系统上的表面场,表示成如下形式:
相应地,总的体积分数φ0(r)为
(2-2)对自由能变分,得到一套自洽的方程组,具体如下:
其中q(r,s)和q+(r,s)为聚合物的末端配分函数,可以用如下修正的扩散方程求解:
其中,初始条件为:q(r,0)=1和q+(r,1)=1,vr为纳米粒子的体积,等于
(2-3)对自洽的方程组编程进行计算机模拟,具体如下:将以上方程编程,自洽迭代,数值模拟求解,可得平衡态时纳米粒子和聚合物的体积分数分数
步骤3.通过程序反复调试,获得产生图案化结构的各种参数,具体如下:取聚合物单体的长度作为单位长度,具体参数取为:聚合物的聚合度n为100,纳米粒子为球形,半径为2,纳米粒子与聚合物的相互作用参数χn=28。系统尺寸为lx×ly×lz,z方向上柱体的高度lz取无限高,lx和ly根据柱体阵列确定;
步骤4.将纳米粒子的体积分数由低到高逐渐增加,从而实现微结构的调控;
步骤5.进一步调节系统和柱体的尺寸,以及纳米粒子与聚合物的体积比,获得其他的图案化结构;
步骤6.设计其他的柱体阵列,重复以上步骤1-步骤5,获得不同的有序微结构。
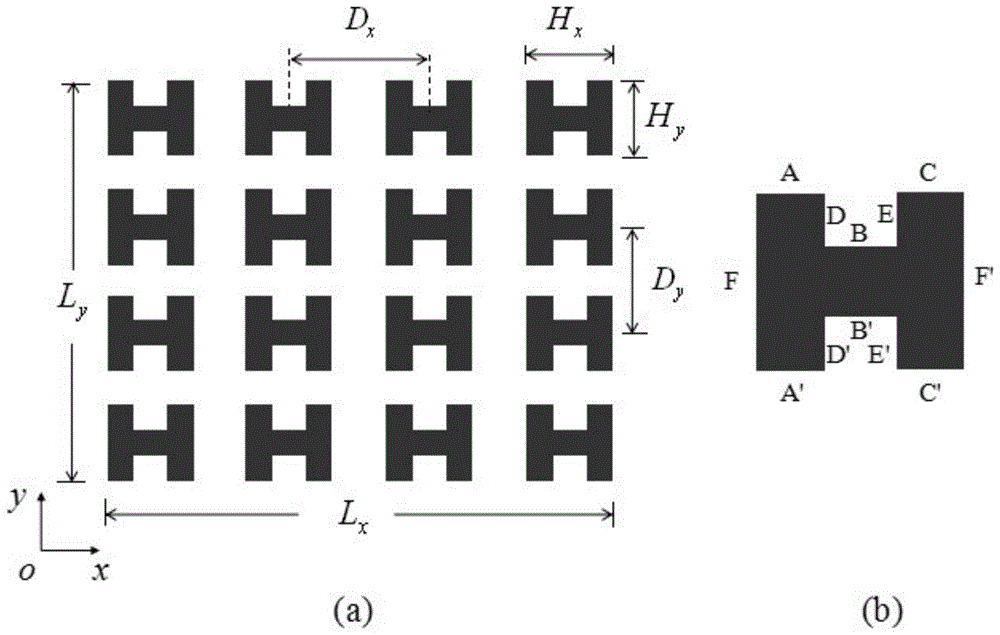
在本实施例中,如图1所示为基于阵列受限自组装有序微结构的制备方法的结构示意图,由俯视图可知,阵列由h形柱体在x方向和y方向各自等间距四方排列而成。柱体表面不可穿透,且与纳米粒子和聚合物既不排斥也不吸引。柱体之间的区域充满了由纳米粒子和聚合物组成的混合物,即纳米粒子/聚合物混合体系受限在h形柱体阵列中。
通过程序调试,最终参数取为:h形柱体的尺寸hx=48,hx=36,取柱体的各边分别为a、b、c、d、e、a’、b’、c’、d’、e’,其中柱体a、b、c和a’、b’、c’边的长度相等,各占hx的1/3;d、e和d’、e’边的长度相等,各占hy的1/3,相邻两个柱体中心之间的距离为dx=dy=64,系统尺寸lx=ly=256,在这个尺寸内分别包含四行四列的h形柱体阵列,利用周期性边界条件,x,y方向上的柱体可以向外周期性延伸。
如图2所示为h形柱体阵列受限下纳米粒子/聚合物混合体系形成的部分有序微结构示意图,纳米粒子的平均体积分数分别对应着(a)0.1,(b)0.12,(c)0.15,(d)0.17。每张图的右边比例尺给出的是图中聚合物的局域体积分数。由于系统不可压缩,用1减聚合物的局域体积分数,则可以得到纳米粒子的体积分数。因此除了图中被柱体占据的部分之外,聚合物0-0.125的标识部分,即图2中的圆圈部分则被纳米粒子占据。
从三维的角度看,纳米粒子形成了圆柱相,圆柱的高度沿着z方向,因此在xy平面里观察到的就是圆形的横截面。当纳米粒子的体积分数比较小的时候,纳米粒子在聚合物中是均匀分布的。随着纳米粒子的增加,纳米粒子与聚合物发生了相分离,自组装形成了有序的微结构。
从图上来看,0.875-1.0的局域体积分数被聚合物占据,当纳米粒子的平均体积分数为0.1时,纳米粒子会聚集在h形柱体b和b’边角落里,一共形成四个圆柱相;当纳米粒子的平均体积分数为0.12时,纳米粒子会继续在h形柱体的a、a’、c和c’边外侧中心附近各形成一个柱状相,在f和f’边外侧分别对称地形成两个圆柱相,因此一共有十二个纳米粒子的圆柱相包围着一个h形柱体;当纳米粒子的平均体积分数为0.15时,纳米粒子又进一步相分离,在h形柱体的f和f’边外侧分别对称地形成四个圆柱相,同时在a、a’、c和c’边外侧分别对称地形成两个圆柱相,这样共有二十个纳米粒子的圆柱相包围着一个h型柱体;当纳米粒子的平均体积分数为0.17时,纳米粒子又会进一步在h形柱体的d、d’、e和e’边外侧各增加一个圆柱相,从而对称地形成两个圆柱相,因此共有二十四个纳米粒子的圆柱相包围着一个h形柱体。
由此可见,当纳米粒子的体积分数比较小的时候,纳米粒子在聚合物中是均匀分布的,随着纳米粒子体积分数的增加,纳米粒子与聚合物发生了相分离,纳米粒子/聚合物混合体系的结构变得越来越复杂,自组装形成了有序的微结构,结构仍保持高度有序。
以上是本发明的优选实施方式,对于本领域的普通技术人员来说不脱离本发明原理的前提下,还可以做出若干变型和改进,这些也应视为本发明的保护范围。
- 还没有人留言评论。精彩留言会获得点赞!