部分连通断层边界的无限大双重介质油藏数学建模方法与流程

本发明属于地质勘探领域，涉及一种部分连通断层边界的无限大双重介质油藏数学建模方法。

背景技术：

目前国内外学者对断层边界的研究及相应的压力和压力导数曲线的分析都是针对封闭断层，而对非封闭断层的研究相对较少，对存在非封闭断层边界的试井解释模型研究也较少。对存在部分连通断层边界的双重介质油藏模型研究也很少。

下面是针对部分连通断层的试井模型方面的研究现状：

1.Bixel等人认为部分连通断层实际上是油层性质在平面上线性不连续的分布，最先对此类线性不连续边界进行研究。

2.1976年，Cinco等人基于点源函数的理论建立了存在无限导流裂缝或者断层边界的理论模型。

3.Stewart和Streltsova通过数值模拟研究了部分连通断层对干扰试井的影响。

4.Yaxely推导了无限大均质油藏中含有部分连通断层模型的解析解。

5.Ambastha进一步研究了复合油藏中存在部分连通断层边界的井底压力响应特征，他引入了无限小表皮的概念，将局部连通断层视为一个无限薄的表皮边界。

6.Abbaszadeh用点源函数方法建立了考虑断层内部流体流动的有限导流断层与储层耦合模型。

目前存在的针对部分连通断层边界的试井模型，是建立在均质地层基础上的；而在实际上，很多存在双重介质特性的地层中，也有部分连通断层边界的存在，现有方法无法正确反应部分连通断层边界的试井状况。

技术实现要素：

本发明目的在于提供一种针对部分连通断层边界的两区无限大双重介质油藏不稳定试井模型的数学建模方法，利用点源函数计算，得到不稳定试井解释模型和相关曲线。

为得到上述目的，本发明采用如下方案：

部分连通断层边界的无限大双重介质油藏数学建模方法，其特征在于，包括以下步骤：

首先考虑部分连通断层边界的两区无限大双重介质油藏的不稳定压力特性；根据假设条件，基于渗流力学基本理论和点源函数计算方法，建立存在部分连通断层边界的两区无限大双重介质油藏的试井解释模型；

根据假设条件，激动井为定产量线源，且以产量q生产，根据渗流力学的相关知识，建立两区渗流微分方程如下：

I区，x＞0：

II区，x＜0：

上式中，为单位体积下基岩向裂缝系统的窜流量，α为形状因子；

引入无因次变量，并将它们代入渗流微分方程及边界条件中，得到两区无限大双重介质油藏中存在部分连通断层的无因次试井解释模型；

然后对数学模型进行求解，并对无因次试井模型式进行Laplace变换，得到类似的渗流微分方程；

与渗流微分方程形式上相似，采用与之相同的求解方法，得到如下压力表达式：

根据Duhamel原理将井储和表皮叠加进去，再利用Stehfest数值反演对其进行拉斯逆变换，编制计算程序，最终得到实空间内的考虑井储和表皮效应影响的井底压力p_wfD(x_D,y_D,t_D)的数值解，从而绘制两区无限大双重介质油藏中存在部分连通断层边界的典型曲线；

上述公式中符号说明如下：

p 压力,MPa

p_i 初始地层压力,MPa

k 渗透率,md

h 厚度,m

w 油藏宽度,m

μ 流体粘度,mpa.s

φ 孔隙度,％

C_t 综合压缩系数,MPa^-1

q 激动井产量,m³/d

t 时间,hr

x x坐标,m

y y坐标,m

a 井的x坐标,m

b 井的y坐标,m

S 井表皮,无因次

S_F 断层表皮,无因次

δ δ函数

α 形状因子

p_D 无因次压降

w_D 无因次宽度

h_D 无因次厚度

η_D 无因次扩散系数

C_D 无因次井筒储集常数

λ 基质到裂缝的窜流系数

ω 储容比

m 傅里叶变量

z 拉普拉斯变换参数。

本发明对存在部分连通断层边界的无限大双重介质油藏进行数学建模，利用点源函数计算，得到不稳定试井解释模型和相关曲线，对部分连通断层边界的无限大双重介质油藏状况分析提供可靠依据。

附图说明

图1距离a_D对典型曲线的影响示意图

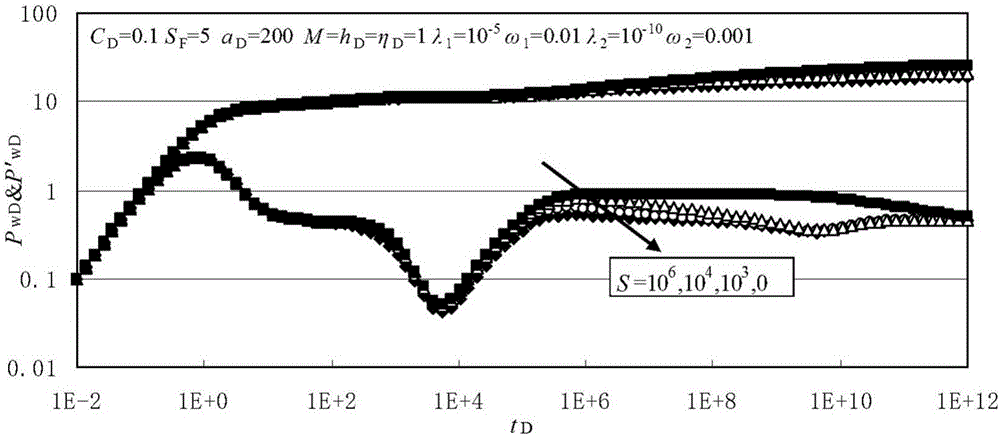
图2界面表皮S对典型曲线的影响示意图

图3窜流系数λ1对典型曲线的影响示意图

图4窜流系数λ2对典型曲线的影响示意图

图5储容比ω1对典型曲线的影响示意图

图6储容比ω2对典型曲线的影响示意图

具体实施方式

为使本发明的目的、技术方案和优点更加清楚，下面本发明中的技术方案进行清楚、完整地描述，显然，所描述的实施例是 本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有作出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

部分连通断层边界的无限大双重介质油藏数学建模方法，其特征在于，包括以下步骤：

首先考虑部分连通断层边界的两区无限大双重介质油藏的不稳定压力特性；根据假设条件，基于渗流力学基本理论和点源函数计算方法，建立存在部分连通断层边界的两区无限大双重介质油藏的试井解释模型；

根据假设条件，激动井为定产量线源，且以产量q生产，根据渗流力学的相关知识，建立两区渗流微分方程如下：

I区，x＞0：

II区，x＜0：

上式中，为单位体积下基岩向裂缝系统的窜流量，α为形状因子；

引入无因次变量，并将它们代入渗流微分方程及边界条件中，得到两区无限大双重介质油藏中存在部分连通断层的无因次试井解释模型；

然后对数学模型进行求解，并对无因次试井模型式进行Laplace变换，得到类似的渗流微分方程；

与渗流微分方程形式上相似，采用与之相同的求解方法，得到如下压力表达式：

根据Duhamel原理将井储和表皮叠加进去，再利用Stehfest数值反演对其进行拉斯逆变换，编制计算程序，最终得到实空间内的考虑井储和表皮效应影响的井底压力p_wfD(x_D,y_D,t_D)的数值解，从而绘制两区无限大双重介质油藏中存在部分连通断层边界的典型曲线；

上述公式中符号说明如下：

p 压力,MPa

p_i 初始地层压力,MPa

k 渗透率,md

h 厚度,m

w 油藏宽度,m

μ 流体粘度,mpa.s

φ 孔隙度,％

C_t 综合压缩系数,MPa^-1

q 激动井产量,m³/d

t 时间,hr

x x坐标,m

y y坐标,m

a 井的x坐标,m

b 井的y坐标,m

S 井表皮,无因次

S_F 断层表皮,无因次

δ δ函数

α 形状因子

p_D 无因次压降

w_D 无因次宽度

h_D 无因次厚度

η_D 无因次扩散系数

C_D 无因次井筒储集常数

λ 基质到裂缝的窜流系数

ω 储容比

m 傅里叶变量

z 拉普拉斯变换参数。

图1所示为断层界面表皮S＝104时，井到断层的距离aD对典型曲线的影响。从图中可知，经过早期井储阶段后，当aD较大，如图中aD＝1000，压力波还没有传到断层边界时，先出现I区裂缝系统的径向流阶段、基岩向裂缝系统的窜流阶段。当压力波到达断层边界，由于界面表皮S的存在，压力导数曲线上翘。当断层边界的影响结束后，出现II区系统的窜流阶段，由于在很短的时间内整个系统就达到了径向流阶段，因此II区双孔介质的反映不明显。

当aD较小，如图中aD＝50时，I区系统的窜流发生在压力波传播断层边界之后。因此，经过井储阶段后，压力导数曲线先出现上翘，之后出现反映I区系统窜流的“凹子”，最后当压力波到达II区，出现II区的窜流及整个系统的径向流阶段。

当aD的值居中，如图中50<aD<1000时，I区系统的窜流与断层界面表皮的影响同时进行，之后曲线的反映与前面讨论的情况类似。

界面表皮S的影响

图2所示为当I区系统的窜流发生在压力波传播到断层边界之前时，断层的界面表皮S对典型曲线的影响。从图中可知，经过井储阶段、I区裂缝系统的径向流阶段、基岩向裂缝系统的窜流阶段后，压力波到达断层边界，界面表皮的影响开始，压力导数曲线出现上升，并且S值越大，压力导数曲线上升越多，当S＝106时，表现出近似于封闭断层的特征，压力导数曲线出现值为1的水平线，并且界面表皮的影响掩盖了II区双孔介质的反映。

窜流系数的影响

图3和图4表示的是I、II区窜流系数λ1和λ2对典型曲线的影响。从图中可以看出，I区窜流系数λ1主要影响压力导数曲线上“凹子”出现时间的早晚，其它参数一定时，λ1越大，“凹子”出现时间越早，界面表皮的影响就发生在I区系统窜流之后，λ1越小，“凹子”出现时间越晚，相应的界面表皮的影响就发生在I区系统窜流之前。同样的，II区窜流系数λ2主要影响导数曲线上第二个“凹子”出现时间的早晚，λ2越大，“凹子”出现时间越早，但总的来说II区窜流影响不明显，这是因为压力波传播到II区后，在很短的时间内，就出现了整个系统的径向流阶段。

图5和图5-6表示的是I区系统的窜流发生在压力波传播到断层边界之前时，I、II区储容比ω1和ω2对典型曲线的影响。从图中可以看出，I区储容比ω1主要影响反映I区窜流的“凹子”形态，ω1越小，过渡段越长，“凹子”就越宽越深，之后出现部分连通断层界面表皮的影响，压力导数曲线上翘。II区储能比ω2主要影响第二个“凹子”形态，但总的来说ω2的影响不如ω1明显。

最后应说明的是：以上实施例仅用以说明本发明的技术方案，而非对其限制；尽管参照前述实施例对本发明进行了详细的说明，本领域的普通技术人员应当理解：其依然可以对前述各实施例所记载的技术方案进行修改，或者对其中部分技术特征进行等同替换；而这些修改或者替换，并不使相应技术方案的本质脱离本发明各实施例技术方案的精神和范围。