一种基于岩石压缩系数计算碳酸盐岩地层孔隙压力的方法与流程

本发明涉及地质勘探领域，尤其涉及一种基于岩石压缩系数计算碳酸盐岩地层孔隙压力的方法。

背景技术：

地层孔隙压力预测对常规油气勘探、非常规油气甜点评价和油气开发有重要的意义，较为准确的地层孔隙压力预测对钻井施工安全、成本效益等也至关重要。

以往针对地层孔隙压力的预测方法，应用广泛且效果较好的经验性的方法有：利用孔隙度和声波测井资料的等效深度法，利用声波和电阻率测井资料的eaton(1972)公式法，利用地震层速度的fillippone(1979)公式法，通过建立声波速度-孔隙度-泥质含量-垂直有效应力等参数之间经验关系的eberhart-phillips模型(1989)和bowers模型(1995)等。这些方法主要是依据taizaghi有效应力原理(描述了土壤或浅部碎屑沉积物的压实过程，适用于浅部地层)，通过建立孔隙压力与不同的孔隙压力响应参数之间的经验关系进而实现对地层孔隙压力的量化评价。这些方法理论上主要适用于压实成岩作用占主体的浅部碎屑岩地层的孔隙压力预测，有些学者尝试用这些方法预测碳酸盐岩地层孔隙压力，取得的效果并不理想，这些方法不适用于碳酸盐岩地层孔隙压力预测的原因在于：①碳酸盐岩成岩作用早期主要是化学压实作用或化学、机械和生物的混合作用，与碎屑岩普遍存在早期机械压实作用存在很大的差异；②寒武纪以来的白云岩主要为碳酸盐岩或灰岩沉积物的白云石化产物，在这种白云岩化、重结晶和溶蚀作用过程中地层流体参与和矿物颗粒体积的变化，可导致岩石中原始孔隙结构发生巨大的改变，使得碳酸盐岩孔渗、孔隙结构等极不均一。

总之，现今碳酸盐岩地层的岩性和物性是地下和地表作用过程中多种类型成岩作用和多重化学反应叠加的结果，从而造成碳酸盐岩地层的岩性和物性等非均质性极强；地下岩石作为多孔弹性介质在围压和孔隙压力的共同作用下的应力-应变必然要达到一定的平衡状态，在这种平衡状态下，围压与孔隙压力的改变会直接影响岩石的物理性质，但致密胶结、非均质性强的碳酸盐岩在纵向上的地球物理参数变化规律难以通过直接观察获取，因此很难发现响应孔隙压力的经验性参数。因此，碳酸盐岩孔隙压力预测一直是国内外研究的难题。

技术实现要素：

本发明针对目前孔隙压力预测方法不适用于复杂非均质的碳酸盐岩地层这一问题，提出一种基于岩石压缩系数的新的孔隙压力计算方法，一定程度上解决了适用于碳酸盐岩岩性致密且极不均匀带来的孔隙压力计算难点，通过岩石物理模拟实验可知，实测孔隙压力与孔隙压力预测量化模型中的关键参数相关性好，此方法理论性强，具有一定的工业应用价值。

本发明为解决现有技术中存在的问题采用的技术方案如下：

一种基于岩石压缩系数计算碳酸盐岩地层孔隙压力的方法，其特征在于，包括如下步骤：

s1：获取待预测碳酸盐岩地层的岩石样品，测试岩石常压孔隙度φ和孔隙体积；

s2：根据岩石样品常压孔隙度，优选一系列样品，采用poropdp-200型覆压孔隙度渗透率测量仪测试岩石地层压实系数，得到不同有效应力下一系列碳酸盐岩样品的岩石地层压实系数cpc和孔隙体积离散值；

s3：根据各个碳酸盐岩岩样孔隙体积与有效应力的离散测试值，对各个样品孔隙体积和有效应力σm的非线性乘幂关系进行拟合，根据对岩样孔隙度、有效应力和岩石地层压实系数进行拟合，得到如下公式：

cpc＝f(φ,σm)

式中，cpc为地层压实系数，σm为有效应力，φ为孔隙度；

s4：根据s3中的拟合公式和biot-willis有效应力定理联立方程组，求解得到物理模拟不同围压、孔隙压力下的岩石孔隙度φ、有效应力σm和地层压实系数cpc；

s5：对所有碳酸盐岩石样品进行全岩x衍射测试，得到组成岩石样品的各矿物体积百分数fi；

s6：根据组成岩石样品的各矿物体积百分数fi，采用voigt-reuss-hill平均模量模型，计算待预测碳酸盐岩地层的岩石基质压缩系数cs；

s7：采用wood模型和patch模型计算岩石样品的孔隙流体压缩系数cf；

s8：根据岩石样品的岩石基质压缩系数cs、孔隙流体压缩系数cf和岩石地层压实系数cpc，计算获得待预测碳酸盐岩地层的孔隙压力p。

进一步地，所述步骤s1中，获取岩石样品孔隙度、孔隙体积的方法为：采用氦气法测试岩石样品孔隙度、孔隙体积。

进一步地，所述步骤s3中，先将每个岩样有效应力测试范围进行扩展，然后通过实测和扩展模拟数据拟合得到岩样孔隙体积、有效应力和岩石地层压实系数的三维曲面关系式，并由拟合曲面关系式与实验测试点和扩展数据点的误差平方和决定系数验证该三维曲面关系式的吻合效果。

进一步地，所述步骤s3中，将孔隙体积转换为孔隙度，其中用到的公式为：

φ＝vp/v

式中，vp为孔隙体积；v为岩石总体积，为实验前岩石基础数据，为先验值。

进一步地，所述步骤s3中，根据对岩样孔隙度、有效应力和岩石地层压实系数进行拟合，采用的拟合方式为非线性最小二乘法。

进一步地，所述步骤s4中，联立得到的方程组为：

式中，σv为围压，为物理模拟实验给定先验值；p′为孔隙压力，为物理模拟实验给定先验值；α为有效应力系数；cs为岩石基质压缩系数。

进一步地，所述步骤s4中方程组的求解步骤如下：

s4-1：由s3中公式整理得到非线性方程组；所述未知数包括：地层压实系数、有效应力和孔隙度；

s4-2：通过粒子群算法搜索一个接近于解的初值；

s4-3：根据初值，采用非线性约束优化方法得到地层压实系数、有效应力和孔隙度的准确解。

进一步地，所述步骤s6中，采用voigt-reuss-hill平均模量模型，计算岩石样品的岩石基质压缩系数cs的计算公式如下：

上式中，ci为岩石样品中n种矿物成分等效模量，i为大于等于1的整数。

进一步地，所述步骤s7中，计算孔隙流体压缩系数cf的计算公式如下所示：

上式中，cif为岩石样品中n种混合物流体成分体积模量，为先验值；xi为岩石样品中n种混合物流体各部分百分含量，为物理模拟实验给定值，i为大于等于1的整数。

进一步地，所述步骤s8中，根据岩石样品的岩石基质压缩系数cs、孔隙流体压缩系数cf和岩石地层压实系数cpc，计算获得待预测碳酸盐岩地层的孔隙压力p的具体方法为：首先根据cs、cf、cpc和φ计算获得复合压缩系数组合项q，计算公式如下所示：

然后，根据下述公式计算获得孔隙压力p：

公式中，φ为岩石孔隙度，为平均主应力，为先验值。

本发明依据岩石多孔弹性力学理论，通过分析岩石压缩系数与孔隙压力、有效应力的本构关系，结合biot-willis有效应力定律建立表征孔隙压力与岩石压缩系数关系的碳酸盐岩孔隙压力预测量化模型；然后通过大量岩石地层压实系数测试和数据模拟，根据拟合得到的岩石地层压实系数与有效应力、孔隙度的定量关系，结合碳酸盐岩岩石物理模拟数据开展孔隙压力预测量化模型验证分析，实测孔隙压力与孔隙压力预测量化模型中的关键参数相关性好，在上述基础上，讨论并提出了模型的校正方法，提高了此方法的适用性。

与现有技术相比，本发明具有如下优点：

针对碳酸盐岩储层非均质性带来的地层孔隙压力计算难点，由于难以直接寻找响应孔隙压力的经验性参数。本发明从岩石物理学角度、基于岩石压缩系数，从理论上建立了反映孔隙压力-岩石压缩系数本构关系的量化模型，这是一种新的孔隙压力预测方法，理论性强，减小了主观认识对孔隙压力预测的影响；且该方法的应用不受岩石化学成岩作用的影响，一定程度上解决了碳酸盐岩岩性致密且极不均匀带来的孔隙压力预测困难，在油气勘探、非常规油气甜点评价和油气开发上具有工业应用价值。

附图说明

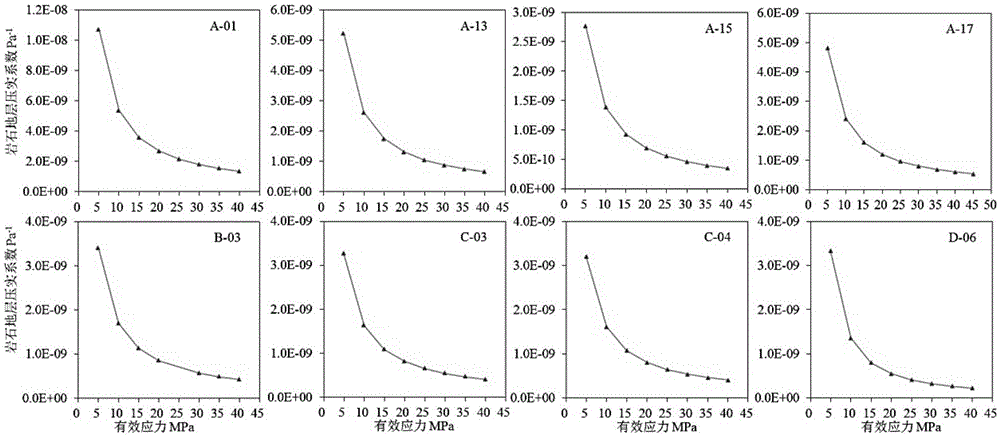
图1为各样品碳酸盐岩干岩样地层压实系数随有效应力增加的变化曲线图；

图2为各样品碳酸盐岩干岩样孔隙体积随有效应力增加的变化曲线图；

图3为碳酸盐岩岩样地层压实系数与孔隙度、有效应力的关系图；

图4为围压固定下碳酸盐岩样品岩石物理模拟孔隙压力与复合压缩系数组合项q的关系图。

具体实施方式

下面通过实施例，并结合附图，对本发明的技术方案作进一步具体的说明，岩石储层类型一般包括碳酸盐岩、碎屑岩等沉积岩储层，本发明以碳酸盐岩储层为例，具体以川东北普光-毛坝地区为例，具体实施过程如下：

一种基于岩石压缩系数计算碳酸盐岩地层孔隙压力的方法，包括如下步骤：

s1：获取待预测碳酸盐岩地层的岩石样品，测试岩石常压孔隙度φ和孔隙体积；

s2：根据岩石样品常压孔隙度，优选一系列样品，如表1所示，采用poropdp-200型覆压孔隙度渗透率测量仪测试岩石地层压实系数，得到不同有效应力下一系列碳酸盐岩样品的岩石地层压实系数cpc和孔隙体积离散值，如图1所示；

表1川东北普光-毛坝地区5口钻井岩心实验样品信息

s3：根据各个碳酸盐岩岩样孔隙体积与有效应力的离散测试值，对各个样品孔隙体积和有效应力σm的非线性乘幂关系进行拟合(如图2所示，可用excel拟合)；

将每个岩样有效应力测试范围由0mpa～45mpa扩展到0mpa～150mpa，通过实测和模拟数据(图3中的点)拟合得到图3所示的碳酸盐岩岩样地层压实系数与孔隙度、有效应力之间的三维曲面关系，由方程(1)表示：

cpc＝f(φ,σm)(1)

式中，σm为有效应力，φ为孔隙度；

本实施例中施加应力时按5mpa为单位增加，根据50mpa～150mpa范围内的孔隙体积变化，利用公式(2)计算得到50mpa～150mpa范围的模拟地层压实系数：

式中，vp为孔隙体积；

由以下公式计算所得，拟合曲面方程与实验测试点和扩展数据点的误差平方和(sse)为4.66×10^-16，决定系数(r-square)为0.9893，证明拟合曲面方程与实验测试点和扩展数据点的吻合效果好。

sse＝∑(yi-fi)²(3)

式中，为实测数据的平均值，先验值；yi为每个实测数据，先验值；fi为利用公式1计算的预测数据，先验值；sse为误差平方和；sst，总平方和；r-square为决定系数。

s4：根据上述拟合关系式(1)和biot-willis有效应力定理联立公式(6)，得到一个复杂的非线性多元方程组(6)，应用此方程组计算得到物理模拟不同围压、孔隙压力下的岩石孔隙度、有效应力、地层压实系数，如表2所示：

式中，σv为围压，为物理模拟实验给定先验值；p′为孔隙压力，为物理模拟实验给定先验值；α为有效应力系数；cs为岩石基质压缩系数；

表2碳酸盐岩样品(a-01和a-13)物理模拟条件及岩石地层压实系数物理模拟结果

s5：对所有碳酸盐岩石样品进行全岩x衍射测试，得到组成岩石样品的各矿物体积百分数fi；

s6：根据组成岩石样品的各矿物体积百分数fi，采用voigt-reuss-hill平均模量模型，计算待预测碳酸盐岩地层的岩石基质压缩系数cs；

s7：采用wood模型和patch模型计算岩石样品的孔隙流体压缩系数cf；

s8：根据岩石样品的岩石基质压缩系数cs、孔隙流体压缩系数cf和岩石地层压实系数cpc，计算获得待预测碳酸盐岩地层的孔隙压力p。

进一步地，步骤s1中，获取岩石样品孔隙体积的方法为：采用氦气法测试岩石样品孔隙度、孔隙体积。

进一步地，所述步骤s3中，将孔隙体积转换为孔隙度，其中用到的公式为：

φ＝vp/v(7)

式中，vp为孔隙体积；v为岩石总体积，为实验前岩石基础数据，为先验值。

进一步地，步骤s4中，复杂的非线性多元方程组的计算步骤如下：

s4-1：由公式(6)整理得到而非线性方程组；所述未知数包括：地层压实系数、有效应力和孔隙度；

s4-2：通过粒子群算法搜索一个接近于解的初值；

s4-3：根据初值，采用非线性约束优化方法得到地层压实系数、有效应力和孔隙度的准确解。

进一步地，步骤s6中，根据组成岩石样品的各矿物体积百分数fi，采用voigt-reuss-hill平均模量模型，计算岩石样品的岩石基质压缩系数cs的计算公式如公式(8)所示：

上式中，ci为岩石样品中n种矿物成分等效模量，岩石样品中矿物组分压缩系数实验室测定经验值，如表3所示，为先验值，i为大于等于1的整数。

表3碳酸盐岩矿物组分的压缩系数测定经验值

进一步地，步骤s7中，计算孔隙流体压缩系数cf的计算公式如公式(9)所示：

上式中，cif为岩石样品中n种混合物流体成分体积模量，为先验值；xi为岩石样品中n种混合物流体各部分百分含量，为物理模拟实验给定值，i为大于等于1的整数。

进一步地，步骤s8中，根据岩石样品的岩石基质压缩系数cs、孔隙流体压缩系数cf和岩石地层压实系数cpc，计算获得待预测碳酸盐岩地层的孔隙压力p的具体方法为：首先根据cs、cf、cpc和φ计算获得复合压缩系数组合项q，计算公式如公式(10)所示：

然后，根据公式(11)计算获得孔隙压力p：

公式(10)中，φ为岩石孔隙度；公式(11)中为平均主应力，为先验值。

采用本发明实施例的方法，预测得到的岩石样品物理模拟孔隙压力p′与计算所得复合压缩系数组合项q的关系示意图如图4所示；围压不变时，利用干燥、部分饱和、饱和碳酸盐岩岩石物理模拟实验数据结合岩石物性参数计算孔隙压力预测理论模型中的岩石基质压缩系数cs、孔隙流体压缩系数cf和岩石地层压实系数cpc，得到复合压缩系数组合项q与物理模拟孔隙压力具有很好的相关性(相关系数均在0.99以上，如图3所示)；这表明，由碳酸盐岩岩石压缩系数-有效应力-孔隙压力本构关系建立的多孔岩石孔隙压力预测定量模型中，复合压缩系数组合项q可作为计算孔隙压力的关键响应参数，即可进一步利用此模型：公式(11)对碳酸盐岩地层孔隙压力进行预测。

本发明的保护范围并不限于上述的实施例，显然，本领域的技术人员可以对本发明进行各种改动和变形而不脱离本发明的范围和精神。倘若这些改动和变形属于本发明权利要求及其等同技术的范围内，则本发明的意图也包含这些改动和变形在内。