一种页岩气井压窜点位置的判断方法

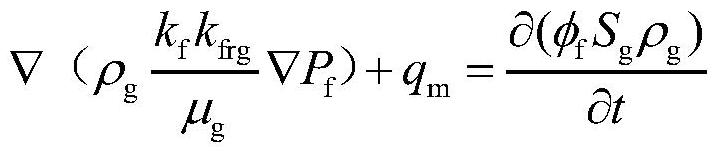
本发明涉及页岩气开发，特别涉及一种页岩气井压窜点位置的判断方法。

背景技术：

1、对于同平台井的非常规气储层进行压裂改造时，相邻井压裂裂缝或天然裂缝可能会连通，导致井间压窜，尤其是对于平台间井距较近的邻井，压窜的可能性增大。压裂井的压裂液通过裂缝沟通进入生产井，导致生产井井底流压增大、产气量下降，降低平台的开发效果。

2、目前，国内外研究学者对于压窜的研究较少，大部分研究是对压窜井生产数据进行压窜程度和恢复速度的简单评价以及通过建立数值模型研究压裂井和生产井之间的裂缝扩展，但数值模拟需要建立精确模型以及模拟过于复杂，目前尚未有明确压窜点位置的研究出现。

3、对进行压窜影响因素分析，因此提出一种页岩气井压窜点位置的判断方法，可为井间压窜程度评价、压窜液量、压窜点的位置确定以及压裂井和生产井后续的压裂施工、增产措施等提供重要依据。

技术实现思路

1、本发明的目的是针对压裂井与生产井之间的压裂液量窜扰，解决压窜点的位置未知这一难题，为压裂井后续的压裂施工、生产井中压裂液的排采指导方向，提供的一种页岩气井压窜点位置的判断方法。

2、本发明提供的一种页岩气井压窜点位置的判断方法，主要步骤思路是：

3、s1、建立物理模型：建立页岩气藏双重介质多级压裂水平井两相渗流物理模型：

4、提出如下假设：

5、(1)页岩储层为双重介质储层，分别为基质解吸扩散系统和裂缝达西流动系统；

6、(2)裂缝系统内为气水两相流动，在该气井生产早期的某一段特定时刻水相饱和度和气相饱和度保持不变；

7、(3)页岩气藏储层为顶底封闭、水平方向无限大边界；

8、(4)储层被多条不可变形的水力裂缝穿透，且水力裂缝之间等间距；

9、(5)流体在水力裂缝及井筒内皆为无限导流且为等温渗流；

10、(6)忽略重力和毛管力的影响；

11、s2、建立数学模型：包括裂缝两相流动方程、基质方程、初始条件、边界条件：

12、基质气相方程：

13、

14、式中：ρm为基质密度，kg/m3；sg为气相饱和度，1；t为时间，h；φm为基质孔隙度，1；qmm为页岩基质化隙解吸扩散量，kg/(m3·s)；

15、基质水相方程：

16、

17、式中：sw为水相饱和度，1；

18、裂缝气相方程：

19、

20、式中：ρg为气相密度，kg/m3；kf为裂缝渗透率，μm2；kfrg为裂缝气相相对渗透率，1；pf为裂缝压力，mpa；μg为气相粘度，mpa·s；qm为水力裂缝中的系统总解吸扩散量，kg/(m3.s)；φf为裂缝孔隙度，1；

21、裂缝水相方程：

22、

23、式中：ρw为水相密度，kg/m3；kfrw为裂缝水相相对渗透率，1；μw为水相粘度，mpa·s；

24、将裂缝气相方程、裂缝水相方程相加得到水力裂缝两相流动方程，引入气水两相拟压力函数，渗流力学原理对其进行化简：

25、两相拟压力函数：

26、

27、式中：m(p)为两相拟压力，kg/(s·m3)；

28、水力裂缝两相流动方程：

29、

30、式中：

31、ct＝ρg0cgsg+ρw0cwsw

32、式中：m(pf)为裂缝两相拟压力，kg/(s·m3)；ct为气水流动参数团，kg/(m3·mpa)；ρg0、ρw0分别为初始状况下的气相密度、气相密度，kg/m3；cg、cw分别为气相压缩系数、水相压缩系数，mpa-1；

33、水力裂缝两相流动方程的拟压力形式：

34、

35、式中：

36、

37、式中：ηf为两相裂缝流动参数团，s-1；

38、同样可以通过上述化简方式来合并基质流动方程，并引入两相拟压力函数，于是基质方程变为：

39、

40、式中：

41、

42、式中：m(pm)为两相裂缝拟压力，kg/(s·m3)；ηm为两相基质流动参数团，s-1；

43、引入无因次变量：

44、无因次两相拟压力为：

45、

46、式中：h为页岩气藏厚度，m；qt为气水两相特征质量流速，kg/s；mi为初始状况下两相拟压力，kg/(s·m3)；

47、无因次时间为：

48、

49、式中：l为水平井长度，m；

50、无因次裂缝拟压力差为：

51、δmdf＝mdi-mdf

52、无因次裂缝拟压力差为：

53、δmdm＝mdi-mdm

54、拟稳态扩散参数团为：

55、

56、式中：psc为标况下地层压力，mpa；t为地层温度，k；tsc为标况下地层温度，k；qsc为标况下质量流速，kg/s；pi为原始地层压力，mpa；

57、非稳态扩散参数团为：

58、

59、对水力裂缝两相流动方程、基质流动方程无因次化：

60、

61、式中：

62、两相储容比为：

63、

64、窜流系数为：

65、

66、式中：d为基质块扩散系数，m2/s；ρsc为标况下气体密度，kg/m3；

67、引入狄拉克三角函数来定位三维笛卡尔坐标下的无因次产量点源：

68、

69、式中：qd为点源无因次产量，kg/s；qg、qw分别为气体体积流速、水体体积流速，m3/s；bg为气体体积系数，1；

70、水力裂缝两相流动方程变为如下形式：

71、

72、对无因次化后的裂缝和基质渗流方程式进行的laplace变换：

73、

74、式中：分别为拉氏变换后两相裂缝无因次拟压力差、两相基质无因次拟压力差；s为laplace变量；

75、对于两相流动中天然微裂缝璧表面扩散量qmf可分为拟稳态扩散和非稳态扩散两类：

76、(1)拟稳态扩散：

77、拟稳态扩散项表达式：

78、

79、式中：g为球形基质块几何因子，1；r为页岩气藏球形基质块半径，m；va、v分别为拟稳态扩散中的气体平衡浓度、水力裂缝中的气体平衡浓度，m3/m3；

80、va和v随时间变化，有：

81、

82、式中：cm为气体质量密度，kg/m3；

83、引出无因次变量：

84、无因次气体平衡浓度为：

85、vad＝va-vi

86、式中：vi为初始状况下水力裂缝中的气体平衡浓度，m3/m3；

87、无因次裂缝气体平衡浓度为：

88、vd＝v-vi

89、无因次气体质量密度为：

90、

91、式中：ci为初始状况下气体质量密度，kg/m3；

92、无因次化拟稳态扩散项表达式为：

93、

94、laplace变化：

95、

96、式中：

97、

98、引入langmuir等温吸附定律：

99、

100、式中：vm为langmuir等温吸附常数，m3/t；pl为langmuir压力，mpa；代入无因次气体平衡浓度表达式，并进行laplace变化，得到：

101、

102、引入解吸系数α：

103、

104、代入可得：

105、

106、由于：

107、

108、代入化简得到：

109、

110、水力裂缝中的系统总解吸扩散量qm＝页岩基质化隙解吸扩散量qmm+天然微裂缝璧表面扩散量qmf：

111、qm＝qmm+qmf

112、代入基质、裂缝两相渗流方程有：

113、

114、式中：

115、

116、(2)非稳态扩散：

117、非稳态扩散项表达式：

118、

119、引入fick第二定律，有：

120、

121、式中：rm为球形基质系统径向半径，m；

122、无因次基质块半径为：

123、

124、非稳态扩散项表达式无因次化：

125、

126、非稳态解吸定解条件：

127、初始条件：

128、

129、边界条件：

130、

131、根据定解条件可以得到：

132、

133、根据双曲函数的定义，上式可以写成如下形式：

134、

135、引入langmuir等温吸附定律和解吸附因子α，得到：

136、

137、可以得到：

138、

139、水力裂缝中的系统总解吸扩散量qm＝页岩基质化隙解吸扩散量qmm+天然微裂缝璧表面扩散量qmf：

140、qm＝qmm+qmf

141、代入基质、裂缝两相渗流方程有：

142、

143、式中：

144、

145、该压裂水平井为顶底封闭、水平方向无限大边界，于是有如下定解条件：初始条件：

146、pf(x,y,z,t)t＝0＝pi

147、内边界条件：

148、

149、外边界条件：

150、

151、引入拟压力函数和无因次定义:

152、无因次x、y、z方向坐标值为：

153、

154、得到：

155、无因次初始条件：

156、

157、内边界条件：

158、

159、外边界条件：

160、

161、s3、求解点源压力响应表达式：通过点源函数法、laplace变换、正交变换推导出点源压力响应表达式：

162、引入特征值法，对于顶底封闭、水平方向无限大边界，其特征方程组为如下形式：

163、

164、求得特征方程组在x、y、z三个方向上的特征值及特征函数：

165、三维特征值：

166、

167、n＝1，2，3…

168、β＝1，2，3…

169、γ＝1，2，3…

170、三维特征函数：

171、

172、通过完备正交系方程可得到x、y、z三个方向上的完备正交性表达式，最后可得三维完备正交性方程：

173、

174、在正交变换情形下的laplace无因次拟压力表达式，对其进行正交逆变换：

175、

176、式中：(xdi，ydi，zdi)为裂缝源点无因次坐标；(xd，yd，zd)为观察点无因次坐标；

177、s4、求解压窜井井底流压：利用叠加原理建立压力响应方程组，通过数值反演计算得到实空间下的井底流压：

178、压裂窜扰的类型包括以下几类：一是压裂井在压裂过程中，虽然没有形成明显的窜扰特征，但通过基质中的孔隙渗流，导致生产井存在短时间的压力异常特征；二是认为注入水诱发天然裂缝开启，将天然裂缝视为高渗网络，连通水平井压裂缝形成窜扰；三是认为受地质特征影响，水力裂缝形成较长的单翼缝特征，从而导致人工裂缝扩展较长，与邻井的人工裂缝连通，导致压窜；由于基质间的渗流通道导致井间干扰在低渗条件下的非常规储层十分有限，因此天然裂缝沟通和人工裂缝连通导致井间干扰造成压窜的说法被大多人所认可，该说法认为压窜点源位于压裂缝上；

179、压裂井开始压裂，t1时压裂井和生产井之间发生压窜，压裂井通过裂缝与生产井的裂缝沟通，压裂液通过裂缝通道进入生产井，生产井井底流压升高，t2时压裂井关井，生产井井底流压下降，假设压窜液量注入质量流速为qp，裂缝通道延伸交于生产井裂缝上的坐标为(xp，yp，zp)，在拉普拉斯变换中，存在性质被称为“时间延迟定理”或“时间平移定理”，时间上的延迟会转化为变换域中的指数因子，将生产井裂缝上的压窜点视为一个离散中心点，压窜点对观察点的无因次拟压力响应表达式：

180、

181、式中：t1d为无因次压窜时间，1；qpd为无因次压窜液量注入质量流速，1；

182、对nf条压裂裂缝沿x轴方向进行离散化，将每条压裂裂缝的左右两翼都等分离散为n个单元，则每条裂缝都被离散为2n个单元，xdi为第i个离散单元的端点坐标，xddi为第i个离散单元的中点坐标，对点源压力响应进行zx裂缝面积分得到裂缝微元的面源压力响应，发生压窜时，地层中包括裂缝上的微元和压窜点点源，利用叠加原理，可得到压窜井laplace空间下的定产量生产的无因次拟压力表达式：

183、

184、基于无限导流的假设，水力裂缝内部任意位置和水平井筒的任意位置压力相同：

185、

186、将i、j取遍裂缝所有微元，可构建2n×nf个方程组，气井产量为已知量，构建微元段产量累加方程：

187、

188、当生产井未压窜时(t<t1)，可得到如下计算矩阵：

189、

190、当生产井处于压窜阶段时(t1≤t<t2)，可得到如下计算矩阵：

191、

192、当生产井处于压窜结束后阶段时(t≥t2)，可得到如下计算矩阵：

193、

194、考虑到表皮效应和井筒储集效应的影响：

195、

196、式中：cd为无因次井筒储集系数，1；sk为表皮系数，1；

197、根据生产井三个阶段的方程组求解不同阶段的井底流压在拉氏空间的解，然后运用stehfest数值反演法，将拉式空间解转化为实空间下的解，有因次化变为井底流压pwf：

198、

199、式中：i为大于0的自然数；n为大于0的偶数；si为laplace空间变量；vi为权重系数；f(si)为反演的函数；

200、s5、确定压窜参数：绘制压窜图版，实测井底流压与图版拟合，可确定压窜液量以及压窜点位置：

201、由s4中的模型可得到压窜井的井底流压曲线图版，根据实测流压数据，先拟合压窜前的部分曲线确定储层参数，后将拟合得到的参数解释结果输入模型中，用于压窜发生后流压资料拟合，可确定压窜液量的注入速度、压窜点坐标。

202、与现有技术相比，本发明具有以下有益效果：(1)合理解释了生产井被压窜后的井底流压变化(2)确定压窜点的位置坐标，为生产井的排采工艺提供指导；(3)确定生产井中被注入的压裂液量，可作为井间压窜程度的一种评价方法。