一种电液伺服阀智能故障诊断方法与流程

1.本发明涉及一种电液伺服阀故障诊断技术，具体涉及一种电液伺服阀智能故障诊断方法。


背景技术：

2.电液伺服阀是液压系统执行机构的中枢神经，如果它能够学习，能够感知系统内部变化的不同或运行状态的差异，实现自我调节，即智能化，则该智能化电液伺服阀堪比人的大脑。
3.目前机载液压系统都只是通过带位移传感器的伺服阀检测阀芯位置来判断伺服阀故障，没有带位移传感器的伺服阀，靠检测连接执行机构(负载设备)管路中压力传感器或流量检测设备变化来判断阀故障。而往往液压系统功能和机载控制部分是不同人员实现，专业性理解与所提需求差异，造成很难达到高度融合判断。特别是对于飞机机载电液伺服阀，在工作中，处在高温、高压、强振动、高动态等极端环境下，因此其采集的信号会受到较大干扰，容易导致有效的信息淹没在噪声之中，使得电液伺服阀的信号采集和分析处理产生极大的困难。
4.随着飞机液压系统的复杂程度越来越高，为保障飞机液压系统的安全和可靠性，电液伺服阀等关键部件所需监测传感器数量相应增加，从而使飞机重量增加，产生飞机的性能下降、油耗增加等一系列问题。


技术实现要素：

5.本发明的目的是提供一种电液伺服阀智能故障诊断方法，用于解决靠检测连接执行机构(负载设备)管路中压力传感器或流量检测设备变化来判断阀故障的问题，同时有效地提升了检测故障地精度及速度。
6.为实现上述目的，本发明的技术方案是：一种电液伺服阀智能故障诊断方法，能够快速准确地定位故障点，具体步骤如下：
7.步骤1：采集电液伺服阀关键参数；
8.步骤2：根据电液伺服阀正常工作时的参数的状态建立起一个基准数学模型，该基准数学模型综合各个变量因素的变化特性以及多次电液伺服阀实际运行时的参数状态的参考，从而使该基准数学具有超高的灵活性以及超强的泛化能力，能够对采集到的状态异常的参数进行快速甄别，进而准确地分析出故障地点；另外，为了能够快速地对数据进行处理，在基准模型的基础上建立一个参数训练集，用于对采集到的参数进行快速整理，提高诊断故障的效率；并且该基准数学模型将作为参照模板与生成的电液伺服阀实时数学模型作对比，进行分析运算，从而达到快速诊断的目的；
9.步骤3：在步骤2的基础上再建立几种伺服阀典型故障数学模型，根据发生故障的类型可以将故障分为典型故障与非典型故障，典型故障包括工作边磨损和阀芯卡滞，非典型故障包括油液温度过高、过低，油液压力过高、过低，温度传感器、压力传感器故障、阀线
圈开路；
10.步骤4：参数处理，建立实时数学模型，将从电液伺服阀采集到的关键数据进行参数训练,通过训练能够使采集到的数据快速的建立实时数学模型，从而能够和已经建立好的基准数学模型、典型故障数学模型进行比较；
11.步骤5：将步骤4所生成的实时数学模型与建立好的基准数学模型和典型故障数学模型进行分析对比，最终得出结论。
12.进一步，所述步骤1中采集的电液伺服阀关键参数包括：反馈电流、油液温度、压力和阀芯位移等，这些参数是参与建立伺服阀工作时数学模型的参数，参数的状态能够在一定程度上显示伺服阀的工作状态。
13.进一步，所述步骤3建立的典型故障数学模型对伺服阀故障进行诊断，采用推演出的一个匹配矩阵k，用匹配矩阵k去做匹配分析运算，具体过程如下：
14.step3.1：求出匹配矩阵k，
15.[nwm]
m
×
n
＝[k]
m
×
n
[tfm]
n
×
n
[0016]
[nwm]
m
×
n
为伺服阀正常工作时的状态矩阵，[tfm]
n
×
n
为典型故障时的状态矩阵，
[0017]
step3.2：对匹配阵k的内容进行故障匹配，
[0018][0019]
f1,f2,...,f
m
,f
n
为每种故障状态匹配的矩阵。
[0020]
进一步，所述步骤4对采集的伺服阀参数数据进行处理，过程如下：
[0021]
step4.1：对伺服阀采样数据进行降噪处理，将采集的伺服阀参数数据组成m行n列的矩阵a，进行奇异值分解，分解如下：
[0022][0023]
其中u代表各维度数据之间的相似方向，v则显示了每条数据之间的相似程度，σ是对角矩阵，对角线上的值为奇异值，非零奇异值的个数为矩阵的秩，t为转置符号，m、n为大于1的整数；
[0024]
当选择的各维度数据之间是相关的，则奇异值就会有零值；如不相关，则奇异值均是非零值；选择的各维度数据不相关，且奇异值之间差距较大，则认为有噪声，通过设定数据阈值，将小于该数据阈值的奇异值归零，重新合成矩阵即可消除噪声数据；
[0025]
step4.2：对降噪后的几个主要参数进行处理，
[0026][0027][0028]
[0029][0030]
δ为标准化后的阀芯位移，p为标准化后的压力，t为标准化后的温度，i为标准化后的电流，δ
s
为采样位移，p
s
为采样压力，t
s
为采样温度，i
s
为采样电流，δ
max
为最大阀芯位移，δ
c
为对应给定的阀芯位移，p
max
为最大压力，p
g
为给定压力，t
max
为温度上限，t
e
为环境温度，i
c
为对应给定的温度；
[0031]
step4.3：求解出实时数学模型，
[0032][0033]
为采样矩阵，
[0034]
为模型标准化矩阵；
[0035]
[r
‑
tm]
n
×
n
为实时模型矩阵。
[0036]
进一步，所述步骤5对实时数学模型与典型故障数学模型的对比，过程如下：
[0037]
step5.1：求出实时数学模型与典型故障数学模型的相似矩阵k：
[0038]
[nwm]
m
×
n
＝[k]
m
×
n
[r
‑
tm]
n
×
n
[0039]
step5.2：将矩阵k与匹配阵k进行对比，
[0040]
对比匹配阵和矩阵k中相似度非常高的地方，便可以定位故障点了。
[0041]
本发明具有的优点和有益效果是：
[0042]
1.本发明提出建立一种建立伺服阀实时模型的想法：采样数据经过标准化处理后便可建成一种伺服阀实时模型。相比其他模型，该模型训练参数少、训练速度快，有效地提高了电液伺服阀故障诊断效率和精度。
[0043]
2.本发明不仅可以用于航空领域，同样可转化应用于其他自动化程度较高便于信息采集的工业领域，具有较大的实际应用价值。
附图说明
[0044]
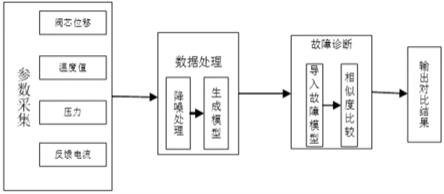
图1是本发明的电液伺服阀智能故障诊断方法结构流程框图；
[0045]
图2为故障处理模型流程图；
[0046]
图3为模型诊断流程图。
具体实施方式
[0047]
下面结合附图对本发明作进一步说明。
[0048]
如图1至图3所示，本发明的一种电液伺服阀的智能故障诊断方法，具体包括以下步骤：
[0049]
第一步，采集电液伺服阀的关键参数，包括温度、压力、电流、阀芯位移。
[0050]
第二步，对采集到的关键参数进行标准化处理，将处理后的参数生成电液伺服阀的实时数学模型。
[0051]
第三步，将实时数学模型与建立好的典型故障数学模型进行匹配运算。
[0052]
第四步，根据第三步的运算结果，输出故障类型。
[0053]
首先介绍第三步所述的建立的典型故障数学模型，具体步骤如下：
[0054]
所述步骤3建立的典型故障数学模型需要对电液伺服阀故障进行诊断，这里并不直接用故障模型去匹配运算而是推演出一个匹配矩阵k，用矩阵k去做匹配分析运算，具体过程如下：
[0055]
step3.1：求出匹配矩阵k，
[0056]
[nwm]
m
×
n
＝[k]
m
×
n
[tfm]
n
×
n
[0057]
[nwm]
m
×
n
为伺服阀正常工作时的状态矩阵，[tfm]
n
×
n
为典型故障时的状态矩阵，
[0058]
step3.2：对匹配阵k的内容进行故障匹配，
[0059][0060]
f1,f2,...,f
m
,f
n
为每种故障状态匹配的矩阵，
[0061]
进一步，所述第四步数据处理的具体步骤如下：
[0062]
step4.1：对电液伺服阀采样数据进行降噪处理，将采集的电液伺服阀参数数据组成m行n列的矩阵a，进行奇异值分解，分解如下：
[0063][0064]
其中u代表各维度数据之间的相似方向，v则显示了每条数据之间的相似程度，σ是对角矩阵，对角线上的值为奇异值，非零奇异值的个数为矩阵的秩，t为转置符号，m、n为大于1的整数；
[0065]
当选择的各维度数据之间是相关的，则奇异值就会有零值；如不相关，则奇异值均是非零值；选择的各维度数据不相关，且奇异值之间差距较大，则认为有噪声，通过设定数据阈值，将小于该数据阈值的奇异值归零，重新合成矩阵即可消除噪声数据。
[0066]
step4.2：对降噪后的数据进行处理，
[0067][0068][0069][0070]
[0071]
δ为标准化后的阀芯位移，p为标准化后的压力，t为标准化后的温度，i为标准化后的电流，δ
s
为采样位移，p
s
为采样压力，t
s
为采样温度，i
s
为采样电流，δ
max
为最大阀芯位移，δ
c
为对应给定的阀芯位移，p
max
为最大压力，p
g
为给定压力，t
max
为温度上限，t
e
为环境温度，i
c
为对应给定的温度。
[0072]
step4.3：求解出实时数学模型，
[0073][0074]
为采样矩阵，
[0075]
为模型标准化矩阵；
[0076]
[r
‑
tm]
n
×
n
为实时模型矩阵
[0077]
以及第五步所述实时数学模型与典型故障数学模型的对比，过程如下：
[0078]
step5.1：求出实时模型与典型故障数学模型的相似矩阵k：
[0079]
[nwm]
m
×
n
＝[k]
m
×
n
[r
‑
tm]
n
×
n
[0080]
step5.2：将矩阵k与匹配阵k进行对比，
[0081]
对比匹配阵和矩阵k中相似度非常高的地方，便可以定位故障点了。