一种基于短时傅里叶变换的空压机故障诊断方法和系统与流程

1.本发明涉及空压机技术领域，特别涉及一种基于短时傅里叶变换的空压机故障诊断方法和系统


背景技术：

2.目前在空压机的状态监测与故障诊断过程中，考虑到检测变量数目庞大且变量之间存在高相关性、故障类型多且故障表现形式的多样性和重叠性的特点，很难采用传统建模的方式构建数学模型。另外，随着实时历史数据库在炼化企业系统中的应用，存储了空压机等关键设备在不同工况下的海量监测数据，针对空压机振动数据，可以利用快速傅里叶变换(fft)、小波变换(wt)、经验模态分解(emd)等现有技术，然而现有技术存在如下技术问题：传统空压机故障诊断方法依赖人工经验，手动提取特征，诊断率不高。空压机设备的故障诊断建立在有效的诊断模型上，虽然取得了一定的效果，但考虑到空压机实际工况中，传感器采集的数据是非线性、非平稳的信号数据，若采用传统网络算法人工选取特征数据会有不确定性并且复杂度极高，难以达到期望的效果。


技术实现要素：

3.本发明其中一个发明目的在于提供一种基于短时傅里叶变换的空压机故障诊断方法和系统，所述方法和系统利用短时傅里叶变换(stft)对空压机震动信号进行分析，并利用主成分分析法将获取的高维频谱转化到低维的特征空间，利用所述主成分分析法得出的少量的多元变量可以更好的揭示非线性、非平稳数据特征，避免人工特征提取带来的特征缺失和特征提取复杂度太高的问题。
4.本发明另一个发明目的在于提供一种基于短时傅里叶变换的空压机故障诊断方法和系统，所述方法和系统利用卷积神经网络模型(cnn)针对非线性、非平稳性和故障类型多的震动特点可以实现自适应的提取特征，从而提高所述空压机故障检测的准确率。
5.本发明另一个发明目的在于提供一种基于短时傅里叶变换的空压机故障诊断方法和系统，所述方法和系统通过所述卷积神经网络模型(cnn)对经过主成分分析法转换得到的二维时频特征进行自适应学习，利用训练集和测试集确定模型参数实现空压机故障诊断，相比于传统的机器学习模型，本发明卷积神经网络模型结合具有隐含多元特征的二维视频具有更好的泛化能力和更好的空压机故障判断准确率。
6.为了实现至少一个上述发明目的，本发明进一步提供一种基于短时傅里叶变换的空压机故障诊断方法，所述方法包括：
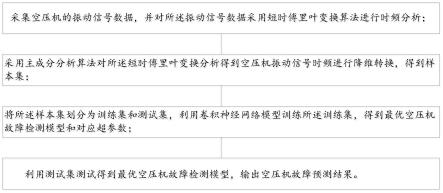
7.采集空压机的振动信号数据，并对所述振动信号数据采用短时傅里叶变换算法进行时频分析；
8.采用主成分分析算法对所述短时傅里叶变换分析得到空压机振动信号时频进行降维转换，得到样本集；
9.将所述样本集划分为训练集和测试集，利用卷积神经网络模型训练所述训练集，
得到最优空压机故障检测模型和对应超参数；
10.利用测试集测试得到最优空压机故障检测模型，输出空压机故障预测结果。
11.根据本发明其中一个较佳实施例，所述采集空压机的振动信号数据包括正常数据和异常数据，所述正常数据和异常数据构成原始数据，对所述原始数据进行数据预处理，其中所述数据预处理的方法包括：将原始数据进行z-score标准化处理，得到服从正态分布的第一数据集。
12.根据本发明另一个较佳实施例，所述数据预处理的方法还包括：设置固定时间步长的时间窗口，通过所述时间窗口按照时间顺序切割经过标准化处理的所述第一数据集，切割后得到多个固定时长样本信号。
13.根据本发明再一个较佳实施例，在完成所述样本信号集后，采用所述短时傅里叶算法对所述样本信号进行时频分析，得到样本信号的时频谱，用于构建样本集，其中所述短时傅里叶算法包括：
[0014][0015]
其中f(t)为时域信号；*表示复共轭；g(t-τ)为中心位于τ时刻的时间窗口，t为时间，e为自然常数，w为角频率，j为虚单位。
[0016]
根据本发明另一个较佳实施例，所述主成分分析算法包括：将所述原始数据设置变量数据和观测量数据，其中配置变量数据的个数为m，观测量数据为n，x为样本信号时频谱数据集，则x∈rm×n；进一步计算所述样本信号时频谱数据集的协方差矩阵：t表示转置矩阵；进一步对所述协方差的特征值进行分解，得到特征值和特征向量。
[0017]
根据本发明再一个较佳实施例，进一步从所述协方差中分解得到的特征值中提取最大的r个特征值，以及r个最大特征值对应的特征向量(p1，p2，p3…
pr)，将所述所有的特征向进行z-score标准化处理，得到标准化的特征向量矩阵p。
[0018]
根据本发明另一个较佳实施例，根据所述标准化的特征向量矩阵p，进一步计算新的样本集，其中原样本集中样本为xi，新样本计算方法为：yi＝p
t
xi；
[0019]
其中yi表示新样本，其中新样本集合为d＝(y1，y2，y3...ym)。
[0020]
根据本发明再一个较佳实施例，所述最优空压机故障检测模型和对应的超参数的获取方法包括：
[0021]
构建卷积神经网络依次连接的输入层、第一卷积层、第一池化层、第二卷积层、第三卷积层、第二池化层、全连接层和输出层；通过第一卷积层设置的卷积核对输入层的二维特征图进行卷积计算，并对卷积结果进行激活后在所述第一池化层进行固定尺寸和步长的池化操作，第一池化层输出池化结果到的第二卷积层进行卷积，将所述第二卷积层卷积结果输入到第三卷积层进行卷积计算，其中第二卷积层和第三卷积层的卷积核个数是第一卷积层的2倍，将第三卷积层卷积结果输入到第二池化层后利用flatten将池化的多维结果一维化，输出一维数据到全连接层，并利用激活函数对全连接层输出结果进行分类，利用随机梯度下降法对模型的参数进行更新得到最优的空压机故障检测模型和对应的超参数。
[0022]
为了实现至少一个上述发明目的，本发明进一步提供一种基于短时傅里叶变换的空压机故障诊断系统，所述系统执行上述一种基于短时傅里叶变换的空压机故障诊断方法。
[0023]
本发明进一步提供他一种计算机可读存储介质，所述计算机可读存储介质保存计算机程序，所述计算程序可被处理器执行上述一种基于短时傅里叶变换的空压机故障诊断方法。
附图说明
[0024]
图1显示的是本发明一种基于短时傅里叶变换的空压机故障诊断方法的流程示意图。
[0025]
图2显示的是本发明中空压机诊断的模型训练和测试方法流程示意图。
[0026]
图3显示的是本发明中卷积神经网络模型训练示意图。
具体实施方式
[0027]
以下描述用于揭露本发明以使本领域技术人员能够实现本发明。以下描述中的优选实施例只作为举例，本领域技术人员可以想到其他显而易见的变型。在以下描述中界定的本发明的基本原理可以应用于其他实施方案、变形方案、改进方案、等同方案以及没有背离本发明的精神和范围的其他技术方案。
[0028]
可以理解的是，术语“一”应理解为“至少一”或“一个或多个”，即在一个实施例中，一个元件的数量可以为一个，而在另外的实施例中，该元件的数量可以为多个，术语“一”不能理解为对数量的限制。
[0029]
请结合图1-图3，本发明公开了一种基于短时傅里叶变换的空压机故障诊断方法和系统，其中所述方法包括如下步骤：首先需要采集空压机的振动数据，所述空压机振动数据利用振动传感器采集，将所述所述振动传感器安装于所述空压机指定检测位置，并和所述振动传感器建立通讯连接，用于实时采集空压机振动信号原始数据。在获取所述振动信号数据后，进一步对所述振动信号数据进行数据预处理，其中所述数据预处理方法包括：采用短时傅里叶变换算法(stft)算法对所述振动信号数据进行时频谱分析，用于构建振动信号数据的时频谱样本数据，进一步采用主成分分析(principal component analysis，pca)算法将所述时频谱样本数据的高维时频谱转换到低维的特征空间，进一步将所述低维的特征作为样本集，将所述样本集划分为训练集和测试集，构建卷积神经网络模型，将所述训练集输入到所述卷积网络模型中训练，通过调整模型参数获得最佳的空压机故障检测模型，并通过测试集输出测试结果。
[0030]
具体而言，所述数据预处理方法还包括，将采集到的振动信号原始数据进行标准化处理，其中采用z-score方法将所述原始数据进行标准化处理，由于振动数据的方向不同，且在不同方向上振幅、频率大小和相位不同，并且在不同方向上进行故障判别时需要根据其检测到的最大振幅、频率和相位进行计算，利用所述z-score方法将不同方向上的振幅、频率和相位进行标准化后得到满足均值为0，标准差为1的标准正态分布，也就是说，通过所述z-score方法对所述原始数据进行标准化后可以克服不同数量级或不同评价标准的数据转换到相同数量级或相同的评价体系中，因此经过所述z-score方法标准化的数据可以实现数据之间规范化的值域，提高数据之间的可比性。其中所述z-score方法标准化包括：获取所述原始振动数据中不同方向上振幅和频率数据，计算每个方向上振幅、频率和相位的平均值ui，并计算每个方向上振幅、频率和相位的标准差si，获取当前对应方向上的观
测值xi，z-score标准化公式为：pi＝(x
i-ui)/si，其中i表示方向。在完成所述振动信号数据的标准化后，进一步设置固定时长(步长)的时间窗口，比如时间窗口步长可以设置为2-3秒，将所述标准化的振动信号数据切割为不同的样本数据，所述时间窗口切割完当前时段内的标准化数据后，进一步首尾连续地截取下一个所述时间窗口步长的标准化数据，直到所有时间段的标准化数据都切割完毕。进一步对所有的样本数据采用短时傅里叶变换(stft)进行分析，得到样本数据信号的时频谱，所述短时傅里叶变换的公式包括：
[0031][0032]
其中f(t)为时域信号；*表示复共轭；g(t-τ)为中心位于τ时刻的时间窗口，t为时间，e为自然常数，w为角频率，j为虚单位。所述傅里叶变换后的样本数据集中的时域信号为物理信号(频率、振幅或相位)相对于时间的关系。所述时频谱还包括频域图，其中所述频域图表示以频率为横坐标，以振幅和相位作为纵坐标的关系图。
[0033]
值得一提的是，在完成所述标准化数据的短时傅里叶变换后得到频谱图后，进一步采用主成分分析方法(principal component analysis，pca)对所述频谱图进行降维操作，需要说明的是，所述主成分分析法是一种数据压缩方法，通过少数的主成分解释多变量的方差，从而可以利用所述主成分揭示完整数据的变量信息，并且主成分更好地揭示不相关信息。其中所述主成分分析方法为：设置所述短时傅里叶变换后的观测量数目，其中x∈rm×n，x为样本总数，且n为观测量数目，m为变量数目。进一步计算短时傅里叶变换后的样本协方差：t表示转置矩阵。
[0034]
对所述协方差矩阵进行特征分解，得到特征值和特征向量。所述特征向量和特征值的计算方法包括：如果一个向量v是矩阵a的特征向量，可以表示成下面的形式：ay＝λv其中，λ是特征向量v对应的特征值，一个矩阵的一组特征向量是一组正交向量。对于矩阵a，有一组特征向量v，将这组向量进行正交化单位化，就能得到一组正交单位向量。特征值分解，就是将矩阵a分解为如下式：a＝q∑q-1
，其中，q是矩阵a的特征向量组成的矩阵，∑则是一个对角阵，对角线上的元素就是特征值。获取到所述特征值和特征向量后，进一步从所述特征值和特征向量中取出r个最大的特征值对应的特征向量(p1，p2，p3…
pr)。进一步将所述r个最大特征值对应的特征向量进行标准化，其中标准化可以采用相同的z-score方法，本发明对此不再赘述，将标准化后的特征向量构建特征向量矩阵p＝(p1，p2，p3…
pr)。获取每一个傅里叶变换后的样本数据xi，并根据所述特征向量矩阵计算新的样本：yi＝p
t
xi；
[0035]
通过所述计算的得到的新样本构建新的样本集：d＝(y1，y2，y3…
ym)。
[0036]
在完成所述原始数据预处理生成所述新样本集后，进一步将所述新样本集按照时间顺序进行先后排序，将排序后的新样本集的前80％作为训练集，将排序后的新样本集的后20％作为测试集，进一步构建卷积神经网络模型，将所述训练集输入到所述卷积神经网络模型进行训练，将测试集输入到训练好的卷积神经网络进行测试。
[0037]
值得一提的是，如图3所示，本发明构建的神经网络模型包括输入层、第一卷积层、第一池化层、第二卷积层、第三卷积层、第二池化层、全连接层和输出层，上述所列的层级之间相互连接，构成数据流链接。其中所述输入层为100*100大小的二维特征图，所述二维特征图通过所述主成分分析进行降维后得到，通过输入层输入所述二维特征图后进入到所述
第一卷积层进行卷积操作，在所述第一卷积层中采用实际数量为32个大小为3*3的卷积核进行卷积计算，其中所述卷积核的步长设置为1，具体利用same padding(输出层尺寸＝输入层尺寸)进行卷积计算，最终在所述第一卷积层得到100
×
100
×
32第一卷积结果，进一步对所述卷积结果采用激活函数进行激活，所述激活函数可以任选现有技术中合适的激活函数；将激活后的数据输入到所述第一池化层进行池化，其中所述第一池化层执行尺寸为2*2，步长为2的池化操作，得到50
×
50
×
32第一池化结果；将所述第一池化结果输入到所述第二卷积层中进行卷积计算，其中所述第二卷积层采用双倍64个3*3的卷积和对所述第一池化结果进行卷积计算，其中所述第二卷积层的卷积核步长为1，并且同样采用same padding进行卷积计算，得到50
×
50
×
64的第二卷积结果，将所述第二卷积结果激活后输入到和所述第二卷积层相同配置的第三卷积层，输出第三卷积结果，并对所述第三卷积结果进行激活。
[0038]
进一步将所述第三卷积结果激活后的数据输入到所述第二池化层，在所述第二池化层采用2*2尺寸，步长为2对所述第三卷积结果激活后数据进行池化操作，得到25*25*64的第二池化结果。对所述第二池化结果运用实际几率是0.25的dropout操作，通过该方式即可获得相应的第二池化结果；进一步利用flatten将池化后的多维结果一维化；将所述第二池化结果输入到全连接层进行全连接操作，其中全连接层运用实际数量为256个神经元的全连接层，针对所述程序计算获得的结果开展全连接操作，同时运用专门的激活函数针对所获取的结果开展激活操作；输出层在该部分的处理过程中，运用softmax函数的方案来处理相关的分类数据，对外输出分类结果概率。
[0039]
本发明中，卷积操作的公式为：
[0040][0041]
其中为第i层第j个元素；mj为i-1层特征图的第j个卷积区域；为i-1层的元素；为对应卷积核的权重矩阵；为偏置项。f(x)为激活函数，本发明中优选使用relu函数作为激活函数。
[0042]
在使用前80％的训练集对所述卷积神经网络进行训练后，采用随机梯度下降法进行模型参数的更新，进一步采用反向传播优化模型并且进行有监督调节，最后得到训练模型最优参数。
[0043]
特别地，根据本发明公开的实施例，上文参考流程图描述的过程可以被实现为计算机软件程序。例如，本公开的实施例包括一种计算机程序产品，其包括承载在计算机可读介质上的计算机程序，该计算机程序包含用于执行流程图所示的方法的程序代码。在这样的实施例中，该计算机程序可以通过通信部分从网络上被下载和安装，和/或从可拆卸介质被安装。在该计算机程序被中央处理单元(cpu)执行时，执行本技术的方法中限定的上述功能。需要说明的是，本技术上述的计算机可读介质可以是计算机可读信号介质或者计算机可读存储介质或者是上述两者的任意组合。计算机可读存储介质例如可以是但不限于电、磁、光、电磁、红外线段、或半导体的系统、装置或器件，或者任意以上的组合。计算机可读存储介质的更具体的例子可以包括但不限于：具有一个或多个导线段的电连接、便携式计算机磁盘、硬盘、随机访问存储器(ram)、只读存储器(rom)、可擦式可编程只读存储器(eprom
或闪存)、光纤、便携式紧凑磁盘只读存储器(cd-rom)、光存储器件、磁存储器件、或者上述的任意合适的组合。在本技术中，计算机可读存储介质可以是任何包含或存储程序的有形介质，该程序可以被指令执行系统、装置或者器件使用或者与其结合使用。而在本技术中，计算机可读的信号介质可以包括在基带中或者作为载波一部分传播的数据信号，其中承载了计算机可读的程序代码。这种传播的数据信号可以采用多种形式，包括但不限于电磁信号、光信号或上述的任意合适的组合。计算机可读的信号介质还可以是计算机可读存储介质以外的任何计算机可读介质，该计算机可读介质可以发送、传播或者传输用于由指令执行系统、装置或者器件使用或者与其结合使用的程序。计算机可读介质上包含的程序代码可以用任何适当的介质传输，包括但不限于：无线段、电线段、光缆、rf等等，或者上述的任意合适的组合。
[0044]
附图中的流程图和框图，图示了按照本发明各种实施例的系统、方法和计算机程序产品的可能实现的体系架构、功能和操作。在这点上，流程图或框图中的每个方框可以代表一个模块、程序段、或代码的一部分，该模块、程序段、或代码的一部分包含一个或多个用于实现规定的逻辑功能的可执行指令。也应当注意，在有些作为替换的实现中，方框中所标注的功能也可以以不同于附图中所标注的顺序发生。例如，两个接连地表示的方框实际上可以基本并行地执行，它们有时也可以按相反的顺序执行，这依所涉及的功能而定。也要注意的是，框图和/或流程图中的每个方框、以及框图和/或流程图中的方框的组合，可以用执行规定的功能或操作的专用的基于硬件的系统来实现，或者可以用专用硬件与计算机指令的组合来实现。
[0045]
本领域的技术人员应理解，上述描述及附图中所示的本发明的实施例只作为举例而并不限制本发明，本发明的目的已经完整并有效地实现，本发明的功能及结构原理已在实施例中展示和说明，在没有背离所述原理下，本发明的实施方式可以有任何变形或修改。