两级主簧式非等偏频型渐变刚度板簧应力强度的校核方法与流程

本发明涉及车辆悬架钢板弹簧，特别是两级主簧式非等偏频型渐变刚度板簧应力强度的校核方法。

背景技术：

为了进一步提高车辆在半载情况下的行驶平顺性，可采用两级主簧式渐变刚度板簧，即将原一级渐变刚度板簧的主簧拆分为两级主簧；同时，为了确保主簧的应力强度，通常通过第一级主簧、第二级主簧和副簧初始切线弧高及两级渐变间隙，使第二级主簧和副簧适当提前承担载荷，从而降低第一级主簧的应力，即采用两级主簧式非等偏频型渐变刚度板簧悬架，其中，板簧根部最大应力及强度，特别是第一主簧的应力强度，决定着板簧的使用寿命、悬架可靠性及车辆行驶平顺性和安全性。然而，由于两级主簧式非等偏频渐变刚度板簧的应力强度校核非常复杂，不仅与板簧结构、载荷大小和许用应力有关，而且还与接触载荷及最大厚度板簧的厚度有关，同时，还受各级板簧根部重叠部分等效厚度计算的制约，据所查资料可知，先前一直未能给出两级主簧式非等偏频型渐变刚度板簧应力强度的校核方法，大都是通过试验测试进行加以确定，因此，不能满足车辆行业快速发展及悬架弹簧现代化CAD设计要求。随着车辆行驶速度及其对平顺性和安全性要求的不断提高，对渐变刚度板簧悬架提出了更高要求，因此，必须建立一种精确、可靠的两级主簧式非等偏频型渐变刚度板簧应力强度的校核方法，为两级主簧式非等偏频型渐变刚度板簧强度校核提供可靠的技术方法，为悬架弹簧现代化CAD软件开发奠定可靠的技术基础，满足车辆行业快速发展、车辆行驶平顺性及对渐变刚度板簧的设计要求，提高两级主簧式非等偏频型渐变刚度板簧的设计水平、产品质量和可靠性及车辆行驶安全性；同时，降低产品设计、试验及维修费用，加快产品开发速度。

技术实现要素：

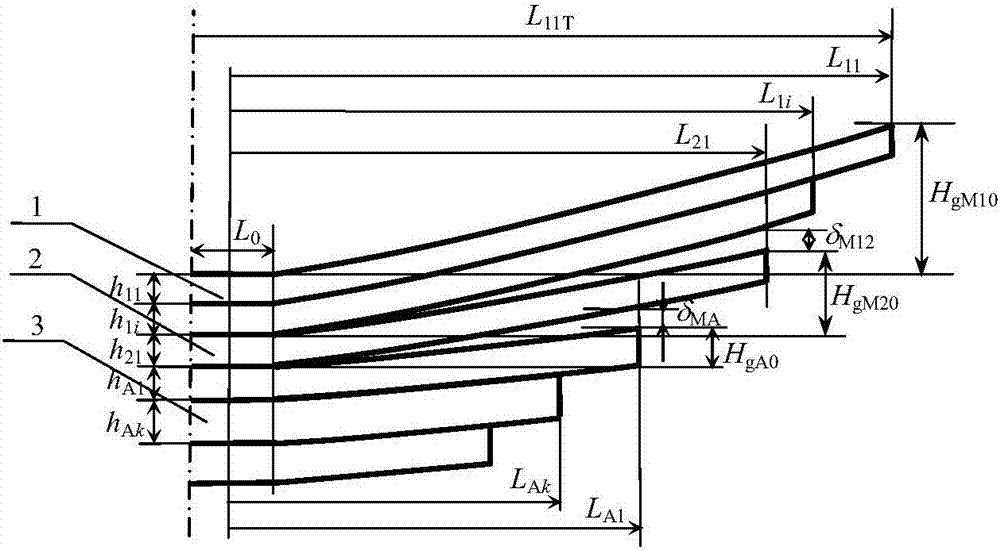
针对上述现有技术中存在的缺陷，本发明所要解决的技术问题是提供一种简便、可靠的两级主簧式非等偏频型渐变刚度板簧应力强度的校核方法，校核流程如图1所示。两级主簧式非等偏频型渐变刚度板簧的一半对称结构如图2所示，是由第一级主簧1、第二级主簧2和副簧3组成。采用两级主簧，并通过第一级主簧1、第二级主簧2和副簧的初始切线弧高H_gM10、H_gM20和H_gA0，在第一级主簧1与第二级主簧2和第二级主簧2与副簧3之间设有两级渐变间隙δ_M12和δ_MA，以提高半载情况下的车辆行驶平顺性。为了确保满足第一级主簧1应力强度设计要求，第二级主簧2和副簧3适当提前承担载荷，悬架渐变载荷偏频不相等，即将板簧设计为非等偏频型渐变刚度板簧。渐变刚度板簧的一半总跨度等于首片主簧的一半作用长度L_11T，骑马螺栓夹紧距的一半为L₀，宽度为b，许用应力为[σ]。第一级主簧1的片数为n₁，第一级主簧各片的厚度为h_1i，一半作用长度为L_1iT，一半夹紧长度L_1i＝L_iT-L₀/2，i＝1,2,…,n₁。第二级主簧2的片数为n₂，第二级主簧各片的厚度为h_2j，一半作用长度为L_2jT，一半夹紧长度L_2j＝L_iT-L₀/2，j＝1,2,…,n₂。副簧3的片数为m，副簧各片的厚度为h_Ak，一半作用长度为L_AkT，一半夹紧长度L_Ak＝L_AkT-L₀/2，k＝1,2,…,m。根据各片板簧的结构参数、骑马螺栓夹紧距、各次开始接触载荷、最大载荷和许用应力，在各级板簧根部最大应力计算的基础上，对两级主簧式非等偏频渐变刚度板簧应力强度进行校核。

为解决上述技术问题，本发明所提供的两级主簧式非等偏频型渐变刚度板簧应力强度的校核方法，其特征在于采用以下校核步骤：

(1)第一级主簧及其与第二级主簧和副簧的根部重叠部分等效厚度的计算：

根据第一级主簧片数n_1i,第一级主簧各片的厚度h_1i，i＝1，2,...,n₁；第二级主簧片数n₂，第二级主簧各片的厚度h_2j,j＝1，2,...,n₂；副簧片数m，副簧各片的厚度h_Ak,k＝1，2,...,m；对第一级主簧的根部重叠部分的等效厚度h_M1e、第一级主簧与第二级主簧的根部重叠部分的等效厚度h_M2e、及主副簧的根部重叠部分的等效厚度h_MAe进行计算，即：

(2)第一、第二级主簧和副簧的最大厚度板簧的厚度h_1max、h_2max和h_Amax的确定：

A步骤：第一级主簧的最大厚度板簧的厚度h_1max确定

根据第一级主簧片数n₁，第一级主簧各片的厚度h_1i，i＝1，2,...,n₁，确定第一级主簧的最大厚度板簧的厚度h_1max，即

h_1max＝max(h_1i)；

B步骤：第二级主簧的最大厚度板簧的厚度h_2max确定

根据第二级主簧片数n₂，第二级主簧各片的厚度h_2j,j＝1，2,...,n₂，确定第二级主簧的最大厚度板簧的厚度h_2max，即

h_2max＝max(h_2j)；

C步骤：副簧的最大厚度板簧的厚度h_Amax确定

根据副簧片数m，副簧各片的厚度h_Ak,k＝1，2,...,m，确定副簧的最大厚度板簧的厚度h_Amax，即

h_Amax＝max(h_Ak)；

(3)两级主簧式非等偏频型渐变刚度板簧的各级板簧根部最大应力的计算：

I步骤：第一级主簧最大载荷下的根部最大应力σ_M1max计算

根据两级主簧式非等偏频型渐变刚度板簧的宽度b，第一级主簧首片的一半夹紧长度L₁₁，第1次开始接触载荷P_k1，第2次开始接触载荷P_k2；最大载荷P_max；步骤(1)中计算得到的h_M1e、h_M2e和h_MAe，步骤(2)中所确定的h_1max，对第一级主簧最大载荷下的根部最大应力σ_M1max进行计算，即

II步骤：第二级主簧最大载荷下的根部最大应力σ_M2max计算

根据两级主簧式非等偏频型渐变刚度板簧的宽度b，第一级主簧首片的一半夹紧长度L₁₁；第1次开始接触载荷P_k1，第2次开始接触载荷P_k2；最大载荷P_max；步骤(1)中计算得到的h_M2e和h_Mae，步骤(2)中所确定的h_2max，对第二级主簧最大载荷下的根部最大应力σ_M2max进行计算，即

III步骤：副簧最大载荷下的根部最大应力σ_Amax计算

根据两级主簧式非等偏频型渐变刚度板簧的宽度b，第一级主簧首片的一半夹紧长度L₁₁；第2次开始接触载荷P_k2，最大载荷P_max，步骤(1)中计算得到的h_MAe，步骤(2)中所确定的h_Amax，对副簧在最大载荷下的根部最大应力σ_Amax进行计算，即

(4)两级主簧式非等偏频型渐变刚度板簧的最大根部应力确定及强度校核：

根据步骤(3)中计算得到的σ_M1max、σ_M2max和σ_Amax，确定两级主簧式非等偏频型渐变刚度板簧的最大根部应力，即

σ_max＝max(σ_M1max,σ_M2max,σ_Amax)；

根据许用应力[σ],如果σ_max<[σ]，即所设计的两级主簧式非等偏频型渐变刚度板簧满足应力强度设计要求；否则，不满足应力强度设计要求。

本发明比现有技术具有的优点

由于两级主簧式非等偏频渐变刚度板簧的应力计算非常复杂，不仅与板簧结构和载荷大小有关，而且还与接触载荷有关，同时，受各级板簧根部重叠部分等效厚度计算的制约，先前一直未能给出两级主簧式非等偏频型渐变刚度板簧应力强度的校核方法，大都是通过应力试验进行加以确定，因此，不能满足车辆行业快速发展及悬架弹簧现代化CAD设计要求。本发明可根据各片第一级主簧、第二级主簧和副簧的结构参数、骑马螺栓夹紧距、各次开始接触载荷、最大载荷及许用应力，在各级板簧根部最大应力计算的基础上，对两级主簧式非等偏频渐变刚度板簧应力强度进行校核。通通过样机的ANSYS建模仿真和加载应力试验可知，本发明所提供的两级主簧式非等偏频型渐变刚度板簧应力强度的校核方法是正确的，为两级主簧式非等偏频型渐变刚度板簧强度校核提供了可靠的技术方法。利用该方法可确保满足板簧应力强度设计要求，提高产品设计水平、质量和可靠性及车辆行驶安全性；同时，还可降低设计及试验费用，加快产品开发速度。

附图说明

为了更好地理解本发明，下面结合附图做进一步的说明。

图1是两级主簧式非等偏频型渐变刚度板簧应力强度的校核流程图；

图2是两级主簧式非等偏频渐变刚度板簧的一半对称结构示意图。

具体实施方案

下面通过实施例对本发明作进一步详细说明。

实施例：某两级主簧式非等偏频渐变刚度板簧的宽度b＝63mm，骑马螺栓夹紧距的一半L₀＝50mm。第一级主簧片数n₁＝2，第一级主簧各片的厚度h₁₁＝h₁₂＝8mm，第一级主簧各片的一半作用长度分别L_11T＝525mm，L_12T＝450mm；一半夹紧长度分别为L₁₁＝L_11T-L₀/2＝500mm，L₁₂＝L_12T-L₀/2＝425mm。第二级主簧片数n₂＝1，厚度h₂₁＝8mm，一半作用长度L_21T＝350mm，一半夹紧长度L₂₁＝L_21T-L₀/2＝325mm。副簧片数m＝2，副簧各片的厚度h_A1＝h_A2＝13mm；副簧各片的一半作用长度分别为L_A1T＝250mm，L_A2T＝150mm；副簧各片的一半夹紧长度分别为L_A1＝L_A1T-L₀/2＝225mm，L_A2＝L_A2T-L₀/2＝125mm。第1次开始接触载荷P_k1＝1851N，第2次开始接触载荷P_k2＝2602N。最大载荷P_max＝7227N，许用应力[σ]＝600MPa。根据各片板簧的结构参数、骑马螺栓夹紧距、各次开始接触载荷、最大载荷及许用应力，对该两级主簧式非等偏频渐变刚度板簧应力强度进行校核。

本发明实例所提供的两级主簧式非等偏频型渐变刚度板簧应力强度的校核方法，其校核流程如图1所示，具体校核步骤如下：

(1)第一级主簧及其与第二级主簧和副簧的根部重叠部分等效厚度的计算：

根据第一级主簧片数n₁＝2,第一级主簧各片的厚度h₁₁＝h₁₂＝8mm；第二级主簧片数n₂＝1，厚度h₂₁＝8mm；副簧片数m＝2,副簧各片的厚度h_A1＝h_A2＝13mm；对第一级主簧的根部重叠部分的等效厚度h_M1e、第一级主簧与第二级主簧的根部重叠部分的等效厚度h_M2e、及主副簧的根部重叠部分的总等效厚度h_MAe进行计算，即：

(2)第一、第二级主簧和副簧的最大厚度板簧的厚度h_1max、h_2max和h_Amax的确定：

A步骤：第一级主簧的最大厚度板簧的厚度h_1max确定

根据第一级主簧片数n₁＝2，第一级主簧各片的厚度，h₁₁＝h₁₂＝8mm，确定第一级主簧的最大厚度板簧的厚度h_1max，即

h_1max＝max(h₁₁,h₁₂)＝8mm；

B步骤：第二级主簧的最大厚度板簧的厚度h_2max确定

根据第二级主簧片数n₂＝1，厚度h₂₁＝8mm，确定第二级主簧的最大厚度板簧的厚度h_2max，即

h_2max＝max(h₂₁)＝8mm；

C步骤：副簧的最大厚度板簧的厚度h_Amax确定

根据副簧片数m＝2，副簧各片的厚度h_A1＝h_A2＝13mm，确定副簧的最大厚度板簧的厚度h_Amax，即

h_Amax＝max(h_A1,h_A2)＝13mm。

(3)两级主簧式非等偏频型渐变刚度板簧的各级板簧根部最大应力的计算

I步骤：第一级主簧最大载荷下的根部最大应力σ_M1max计算

根据两级主簧式非等偏频型渐变刚度板簧的宽度b＝63mm，第一级主簧首片的一半夹紧长度L₁₁＝500mm；第1次开始接触载荷P_k1＝1850N，第2次开始接触载荷P_k2＝2600N，最大载荷P_max＝7227N；步骤(1)中计算得到的h_M1e＝10.1mm、h_M2e＝11.5mm和h_MAe＝18.1mm，步骤(2)中所确定的h_1max＝8mm，对第一级主簧最大载荷下的根部最大应力σ_M1max进行计算，即

II步骤：第二级主簧最大载荷下的根部最大应力σ_M2max计算

根据两级主簧式非等偏频型渐变刚度板簧的宽度b＝63mm，第一级主簧首片的一半夹紧长度L₁₁＝500mm，第1次开始接触载荷P_k1＝1850N，第2次开始接触载荷P_k2＝2600N，最大载荷P_max＝7227N；步骤(1)中计算得到的h_M2e＝11.5mm和h_MAe＝18.1mm，步骤(2)中所确定的h_2max＝8mm，对第二级主簧最大载荷下的根部最大应力σ_M2max进行计算，即

III步骤：副簧最大载荷下的根部最大应力σ_Amax计算

根据两级主簧式非等偏频型渐变刚度板的宽度b＝63mm，第一级主簧首片的一半夹紧长度L₁₁＝500mm，第2次开始接触载荷P_k2＝2600N，最大载荷P_max＝7227N；步骤(1)中计算得到的h_MAe＝18.1mm，步骤(2)中所确定的h_Amax＝13mm，对副簧最大载荷下的根部最大应力σ_Amax进行计算，即

(4)两级主簧式非等偏频型渐变刚度板簧的最大根部应力确定及强度校核：

根据步骤(3)中计算得到的σ_M1max＝585.7MPa、σ_M2max＝241.6MPa和σ_Amax＝241.5MPa，确定两级主簧式非等偏频型渐变刚度板簧的最大根部应力，即

σ_max＝max(σ_M1max,σ_M2max,σ_Amax)＝σ_M1max＝585.7MPa；

可知，σ_max<[σ]，即该两级主簧式非等偏频型渐变刚度板簧满足应力强度设计要求。

通过样机的ANSYS建模仿真和加载应力试验可知，本发明所提供的两级主簧式非等偏频型渐变刚度板簧应力强度的校核方法是正确的，为两级主簧式非等偏频型渐变刚度板簧强度校核提供了可靠的技术方法。利用该方法可确保满足板簧应力强度设计要求，提高产品设计水平、质量和可靠性及车辆行驶安全性；同时，降低设计及试验费用，加快产品开发速度。