一种计及齿背接触特性的圆柱齿轮双齿面修形方法与流程

本发明广泛涉及齿轮传动系统的振动噪声抑制领域，特别涉及一种计及齿背接触特性的圆柱齿轮双齿面修形方法。

背景技术：

随着现代工业不断朝着高速、重载方向的发展，圆柱齿轮传动系统在其中表现出的振动噪声等问题引起国内外学者的广泛关注，各种减振降噪设计控制方法也应运而生，齿面修形作为有效的齿面振动抑制方法，一直是齿轮设计阶段进行振动抑制的重要方法。由于斜齿轮的啮合线沿齿面倾斜分布，单一的齿廓修形或齿向修形很难较好地解决齿面偏载、啮合冲击、振动噪声等问题，随着加工制造技术的不断发展，三维修形、拓扑修已形成为主流的齿面修形技术。

圆柱齿轮在高速运转状态下，会发生齿面-脱啮-齿背的啮合状态转换，从而表现处强烈的非线性特性，传统修形一般均只对正常啮合齿面进行修形，而齿背之间的接触特性明显不同于齿面正常啮合，齿背接触质量也关系着传动系统综合噪声品质。

因此有必要对正常啮合齿面和齿背啮合齿面同时进行齿面修形设计，提出一种计及齿背接触特性的圆柱齿轮双齿面修形方法，以期望达到更好的减振降噪效果。

技术实现要素：

本发明的目的在于提供一种计及齿背接触特性的圆柱齿轮双齿面修形方法，以期望达到更好的减振降噪效果，其中通过考虑增/减速状态的轮齿承载接触分析(loadcontactanalysis，ltca)计算圆柱斜齿轮动态啮合刚度，进一步建立考虑齿面/齿背啮合刚度、线外啮合冲击激励的高转速圆柱斜齿轮传动系统非线性振动模型，并在此基础上建立一套同时计及齿面、齿背接触状态的双齿面减振修形优化方法。

充分利用现有ltca计算程序以遗传算法的高效便捷性，在此基础上结合齿面三维修形相关技术基础编制一套合理高效的同时计及齿面、齿背接触状态的双齿面减振修形优化计算程序。

本发明针对圆柱斜齿轮齿背啮合接触状态的啮合机理模型，建立考虑实际动态啮合刚度、线外啮入冲击、齿侧间隙激励因素的高转速圆柱斜齿轮非线性振动模型。

本发明在圆柱斜齿轮非线性振动模型的基础上，利用牛顿力学定律，建立包含轴向、啮合切向以及扭转方向振动位移的动力学方程，采用龙科库塔方法求解圆柱斜齿轮齿面啮合相对振动。

本发明选取圆柱斜齿轮齿面振动加速度为目标，对斜齿轮接触齿面以及接触齿背双齿面进行三维修形，并采取改进的自适应遗传算法进行修形参数设计优化。

本发明的有益效果：

本发明实现了结合高速圆柱斜齿轮齿背啮合机理的接触模型，选用自适应遗传算法对双齿面参数进行修形优化设计，为进一步降低高速圆柱齿轮传动系统振动噪声、提升传动品质，提供了一种有效的齿面修形方法，该方法在减缓圆柱齿轮振动的同时，也增大了系统可供稳定工作的转速区间范围，具有较好的工程实际应用价值。

附图说明

图1为圆柱斜齿轮模型；

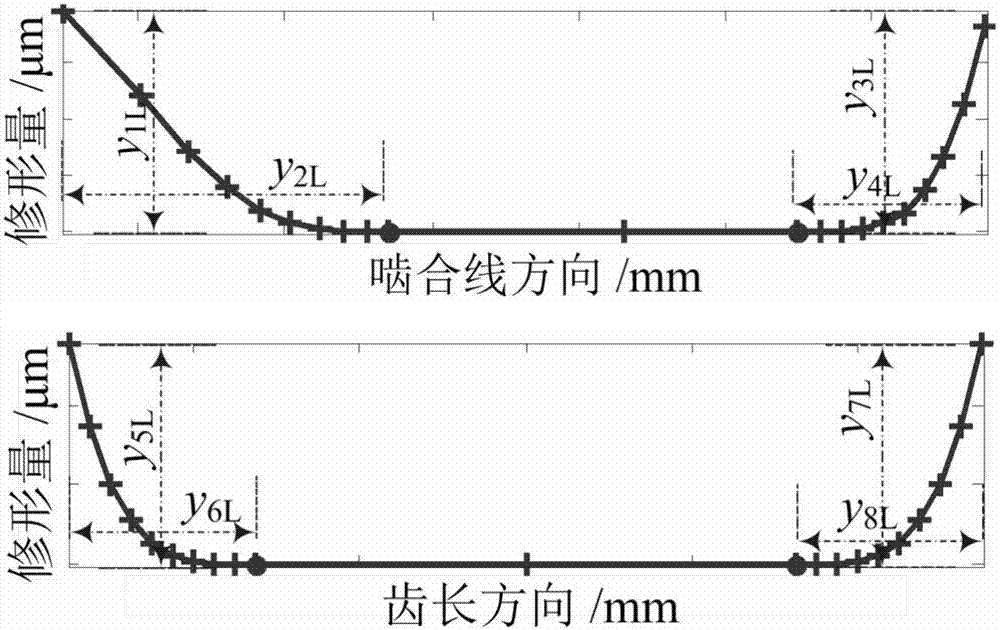
图2为齿面修形参数示意图；

图3为齿背修形参数示意图；

图4为双齿面修形优化流程图；

图5为齿面修形前后的齿面时域振动对比；

图6为标准齿面振动分岔图；

图7为单齿面修形振动分岔图；

图8为双齿面修形振动分岔图。

具体实施方式

下面结合附图和实施例对本发明作进一步说明，但本发明的保护范围并不限于此。

1、圆柱斜齿轮传动系统振动激励因素多种多样，其中齿面误差、时变啮合刚度通常被作为主要激励因素予以考虑，在高速斜齿轮中，与转速直接相关的线外啮合冲击力激励则有必要计入，结合图1圆柱斜齿轮啮合模型，建立考虑实际动态啮合刚度、线外啮入冲击、齿侧间隙激励因素的动力学方程组(1)。

其中，[m]、[c]、[k]分别为圆柱斜齿轮的质量矩阵、阻尼矩阵和刚度矩阵，其中[k]中计及了齿背啮合刚度；d²x/dt²、dx/dt、x分别为圆柱斜齿轮的振动加速度向量、速度向量和位移向量；f(t)、fs(t)为外载激振力矢量。

2、图2为正常啮合高速轮齿面三维修形示意图，其中，y1l、y3l、y5l、y7l为修形量；y2l、y4l、y6l、y8l为修形长度；图3为齿背啮合高速轮齿面三维修形示意图，其中，y1r、y3r、y5r、y7r为修形量；y2r、y4r、y6r、y8r为修形长度。

3、综合上述阐述，建立以圆柱斜齿轮齿面振动为目标的双齿面修形优化函数，对图2、图3中的16个齿面修形变量进行优化，建立如式(2)～(4)优化函数。

fc(yij)＝min(arms)...(i＝1,2,...,8；j＝l,r)(2)

式中，fc为给定工况下的优化函数；yij(i＝1,2,…,8；j＝l,r)为齿面和齿背修形参数，具体参见图2、图3；arms为齿面振动均方根值；lymin、lymax、lzmin、lzmax、qymin、qymax、qzmin、qzmax为修形量和修形长度范围；ly0、lz0、qy0、qz0为修形量常数和修形长度常数。

4、采用自适应遗传算法对以齿面振动加速度均方根值为目标的圆柱斜齿轮双齿面修形参数进行优化求解，即可得到双齿面修形最优参数。

归纳本发明，首先建立考虑实际动态啮合刚度、线外啮入冲击、齿侧间隙激励因素的动力学模型；然后建立以圆柱斜齿轮齿面振动为目标的双齿面(齿面、齿背)修形优化函数；并采用改进的自适应遗传算法对以齿面振动加速度均方根值为目标的圆柱斜齿轮双齿面修形参数进行优化求解，到双齿面修形最优参数。具体如图4所示。

实施例

为验证本发明的双齿面修形效果，以表1参数进行实例计算，表1为某单级减速圆柱斜齿轮副参数。

表1

在给定高速轮输入工作转速为8000r/min、低速轮负载扭矩1325n·m工况下，表2、表3分别为高速轮的齿面和齿背修形曲面优化参数结果，表2为正向齿面修形参数优化结果，表3为齿背齿面修形参数优化结果。

表2

表3

在此三维修形优化曲面参数下重新计算轮齿端面啮合线向相对振动加速度如图5，其中振动加速度均方根值双面修形<单面修形<标准齿面，均方根值分别为18.2m/s²、14.7m/s²、12.8m/s²，可见双面修形更有利于减缓高速圆柱斜齿轮的振动噪声。

同样，在图6～图8中给出齿面相对振动随转速变化而表现出来的丰富的分岔特性，其中显示，相较于标准齿面，单面修形齿面振动在1.02e4转速附近的分岔特性消失；进一步，双面修形齿面振动在1.80e4附近的分叉特征消失。也就是说，双面修形齿面在减缓圆柱齿轮振动的同时，也增大了系统可供稳定工作的转速区间范围，具有较好的工程实际应用价值。

上文所列出的一系列的详细说明仅仅是针对本发明的可行性实施方式的具体说明，它们并非用以限制本发明的保护范围，凡未脱离本发明技艺精神所作的等效实施方式或变更均应包含在本发明的保护范围之内。