一种谐波传动的渐开线齿廓修形方法与流程

本发明涉及谐波齿轮技术领域，特别涉及一种谐波传动的渐开线齿廓修形方法。

背景技术：

渐开线齿廓具有传递性能良好、工艺性成熟、加工制造刀具简单等优点，被广泛应用于齿轮传动中。而由于谐波齿轮传动中，柔轮频繁的啮入啮出钢轮，啮合轨迹近似于摆线，导致普通渐开线齿轮在谐波传动中啮合性能差，并且啮合过程中存在尖点接触现象，不利于油膜的形成。传统的渐开线齿廓修型方法建立在willis齿轮基本啮合定理基础上，适用于定轴传动，不适用于谐波齿轮传动。

技术实现要素：

本发明所要解决的技术问题是提供一种谐波传动的渐开线齿廓修形方法，采用本方法对渐开线齿廓进行齿廓修形和齿向修形，柔轮轮齿能弥补渐开线齿轮用于谐波齿轮传动的不足、能增加同时啮合的齿数、能使啮合侧隙更小、能够实现连续传动，能保证加工工艺性和经济性，又能提高啮合性能，综合了各种谐波齿形的优点，从而提高了传动的平稳性。

为解决上述技术问题所采用的技术方案：

一种谐波传动的渐开线齿廓修形方法，沿修形曲线对渐开线齿廓进行修形，点b为修形曲线与渐开线齿面的切点，点e为修形曲线与渐开线齿顶圆的交点，点o为基圆圆心，以射线oa为横坐标建立坐标系xoy，以射线oc为纵坐标轴建立坐标系x1oy1，点a为齿面与基圆的交点，点c为轮齿中心线与齿顶圆的交点；求解修形曲线的步骤如下：

1-1、在坐标系x1oy1中，确定点b和点e的坐标分别为(x1b,y1b)、(x1e,y1e)，以及渐开线在点b处的切线斜率k1b；

1-2、在坐标系x1oy1中，根据齿条近似法原理确定柔轮齿中心点近似运动轨迹曲线方程为

其中，m为柔轮的模量，z2为柔轮的齿数，k为该曲线上任一点的斜率，η＝2ψ，ψ为柔轮齿中心线与中性层曲线的交点的矢径与谐波发生器的长轴之间的夹角；

1-3、将柔轮池中心点近似运动轨迹曲线方程进行平移、旋转和缩放获得同时通过点b和点e的修形曲线，并确定修形曲线在坐标系x1oy1中的参数方程为

其中，λ,χ,τ为修形曲线的参数值，η∈[0,π]；

1-4、联立方程组可求出修形曲线中λ,χ,τ等参数值，以及修形曲线在点b处对应的ηb和在点e处对应的ηe，

1-5、进行坐标系转换，得到修形曲线在坐标系xoy下的参数方程为

其中，η∈[ηb,ηe]。

进一步，坐标系xoy与x1oy1之间的转换矩阵为

其中，θ0＝tanα0-α0，α0为分度圆压力角。

进一步，所述步骤1-1中确定点b在坐标系x1oy1中的坐标步骤如下，

1-1-1、渐开线在坐标系xoy中的参数方程为

齿顶圆在坐标系xoy中的方程为

将上述两个方程联立可得点k在渐开线的滚动角φk为

1-1-2、确定点b的在坐标系xoy中的坐标，弧ka的长度为

同理，弧ba和弧qa的长度分别为

因此弧bk的长度为

即

所以点b在渐开线的滚动角φb为

可求出点b在坐标系xoy中的坐标为

1-1-3、确定点b在坐标系x1oy1中的坐标为

进一步，所述步骤1-1中确定点e在坐标系x1oy1中的坐标方法如下，根据点k的的滚动角可得出展角θk为

θk＝φk-arctanφk

因此

βk＝β0+θ0-θk

所以，点e在坐标系x1oy1中的坐标为

进一步，根据所述步骤1-1-3中点b在坐标系x1oy1中的坐标可得出渐开线在点b处的斜率为

进一步，在齿顶处所述e点的位置通过最大修形量确定，所述最大修形量与柔轮轮齿的模数m有关，取值范围为(0.05m,0.4m)。

有益效果：本方法是基于谐波传动运动学理论对谐波传动渐开线齿廓进行修形，通过谐波齿轮传动运动几何学理论得到柔轮齿中心点的运动轨迹曲线，将该运动轨迹进行缩放和旋转后作为谐波渐开线齿廓的修形曲线，该修形曲线与柔轮齿顶的端点相交，同时又与柔轮齿面相切，从而使柔轮的齿面光滑过渡。采用本方法对柔轮齿廓进行修形，柔轮轮齿能弥补渐开线齿轮用于谐波齿轮传动的不足、能增加同时啮合的齿数、能使啮合侧隙更小、能够实现连续传动，既能保证加工工艺性和经济性，又能提高啮合性能，可广泛应用于谐波齿轮技术领域。

附图说明

图1为齿顶修缘示意图；

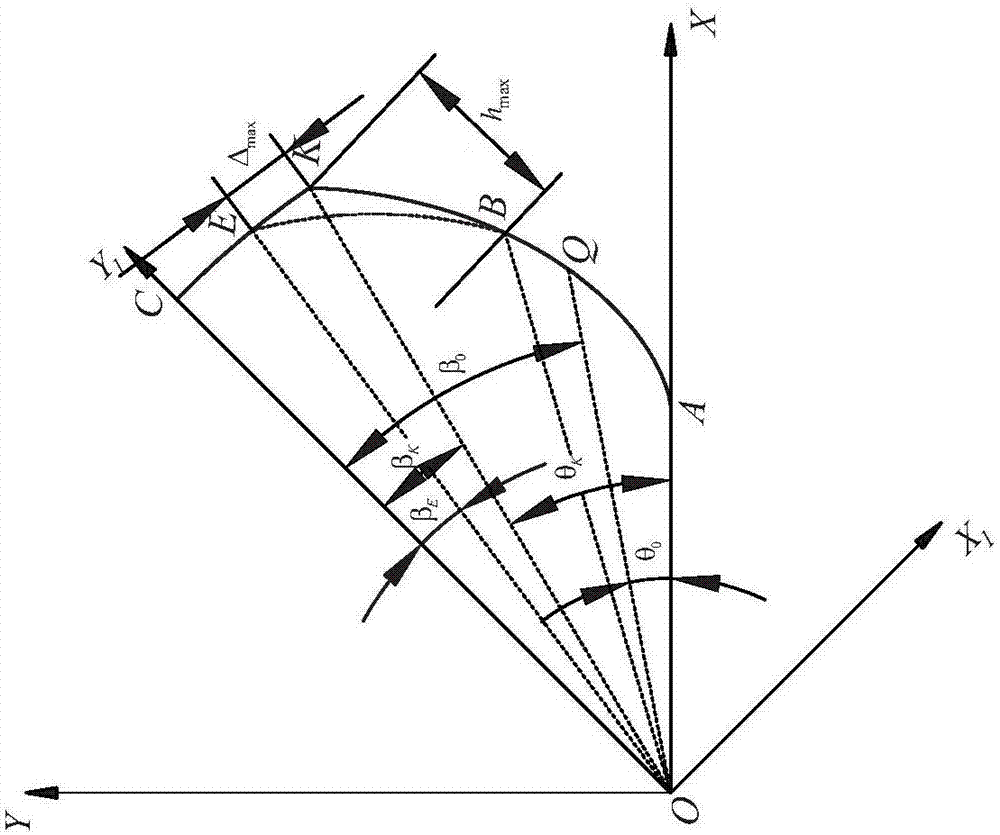
图2为柔轮齿轮右侧修形部分和修形曲线示意图。

具体实施方式

本方法中沿修形曲线对渐开线齿廓进行修形，下面结合图1和图2对本发明修形曲线的求解方法做进一步的说明。

如图1，虚线部分就是修形曲线。如图2，以对柔轮轮齿右侧的渐开线齿廓进行修形为例进行说明，点b为修形曲线与渐开线齿面的交点，点e为修形曲线与齿顶圆的交点，并且在b点处修形曲线与渐开线齿面相切。在齿顶处所述e点的位置通过最大修形量δmax确定，所述最大修形量δmax与柔轮轮齿的模数m有关，最大修形量δmax的取值范围为(0.05m,0.4m)。

点k为修形前齿顶圆与齿面的交点，点q为分度圆与齿面的交点，点a为齿面与基圆的交点，点o为基圆圆心，点c为轮齿中心线与齿顶圆的交点。下文中涉及的符号说明如表1所示。

以点o为坐标原点，以射线oa为横坐标轴建立坐标系xoy，射线oa为坐标系xoy中x轴的正坐标轴，以射线oc为纵轴建立坐标系x1oy1，射线oc为坐标系x1oy1中y1轴的正坐标轴。坐标系xoy与x1oy1之间的转换矩阵为

其中，θ0＝tanα0-α0。

求解修形曲线的步骤如下：

1-1、确定点b和点e在坐标系x1oy1中的坐标分别为(x1b,y1b)、(x1e,y1e)。

设渐开线滚动角为φ，因此渐开线在坐标系xoy中的参数方程为

其中，基圆半径

齿顶圆在坐标系xoy中的方程为

其中，齿顶圆半径

联立渐开线方程和齿顶圆方程可得

从而点k的滚动角φk为

所以，弧ka的长度为

同理，弧ba和弧qa的长度分别为

因此，可以得到弧bk和弧qk的长度分别为

由图2可以得到弧bk长度为

所以

故

点b坐标系xoy中的坐标为：

因此，点b在坐标系x1oy1中的坐标为

同时，对点b的坐标求导可得渐开线在点b处的切线斜率为

另外，根据点k的滚动角φk可得出点k的展角θk为

θk＝φk-arctanφk

因此可得

βk＝β0+θ0-θk

所以点e在坐标系x1oy1中的坐标为

在x1oy1坐标系中，根据齿条近似法原理可得，柔轮齿中心点近似运动轨迹曲线方程为

其中，η＝2ψ，ψ为柔轮齿中心线与中性层曲线的交点的矢径与谐波发生器的长轴之间的夹角。

将上述的近似运动轨迹曲线方程进行平移、旋转和缩放，得到同时通过点b和点e的修形曲线，其在坐标系x1oy1中的参数方程为

其中，η∈[0,π]。

因此，可得到下列五元非线性方程组

通过解上述方程组就可以得到修形曲线中的参数λ,χ,τ的值，并且可以得到修形曲线上点b所对应的ηb和点e所对应的ηe。通过坐标系的转换，可以得到修形曲线在坐标系xoy下的参数方程为：

其中，η∈[ηb,ηe]。

实施例一：

下面结合一个具体的柔轮齿轮的修形曲线进行具体的计算。主要参数选取如下：柔轮齿数z＝60，模数m＝1.3，压力角α0＝20°，齿顶高系数则β0＝π/2z＝0.0262，θ0＝tanα0-α0＝0.0149。设谐波渐开线齿廓修形的最大修形量和修形长度分别为δmax＝0.2m＝0.26，渐开线在坐标系xoy中的参数方程为

其中，基圆半径

齿顶圆坐标系xoy中的方程为

其中，齿顶圆半径

联立渐开线和齿顶圆方程可得

从而得点k的滚动角φk为

因此，弧ka的长度为

同理可得弧ba和弧qa的长度分别为

因此，可以得到弧bk和弧qk的长度分别为

由图2可以得到弧bk长度为

所以

故

所以，在坐标系x1oy1中点b的坐标为

且在坐标系x1oy1中，渐开线在点b处的切线斜率为

另外，根据点k的滚动角φk可得出点k的展角θk为

θk＝φk-arctanφk＝0.0255

因此可得

βk＝β0+θ0-θk＝0.0156

所以点e在坐标系x1oy1的坐标为

将x1b,y1b,k1b,x1e,y1e,m的值代入五元非线性方程组，得到非线性方程

因此可得

λ＝0.2352，χ＝1.6279，τ＝37.7601，ηb＝1.1795，ηe＝2.3136故得到修形曲线在坐标系x1oy1中的参数方程为

通过整理得：

其中，η∈[1.1795,2.3136]。

表1

以上结合附图对本发明的实施方式作了详细说明，但是本发明不限于上述实施方式，在所述技术领域普通技术人员所具备的知识范围内，还可以在不脱离本发明宗旨的前提下作出各种变化。