一种同时生成柔轮与刚轮齿形的谐波齿形设计方法与流程

1.本发明涉及机械传动领域的谐波齿形设计方法，具体涉及一种基于柔轮弹性变形规律，能够同时生成柔轮与刚轮齿形的谐波齿形设计方法。


背景技术：

2.谐波减速器作为一种精密减速器，近年来广泛应用于卫星，雷达，特别是机器人的终端 执行机构等领域。它具有体积小，传动比大，传动精度高，寿命长等特点。谐波齿形设计是 谐波减速器设计中的重要部分，齿形直接影响谐波减速器的承载能力、传动精度和传动平稳 性。国内外专家都对齿形进行了研究，最早由musser提出了谐波减速器概念并申请了专利(专 利号：美国专利us 2906143)，其采用了直齿齿形，该齿形啮合范围较小。目前常用的齿形 有渐开线，双圆弧和s形齿形等，渐开线齿形易于加工，但存在边缘接触，不利于油膜形成。 双圆弧齿形目前已有大量相关专利(专利号：中国专利cn200610112756.0， cn201410309903.8，cn201710436032.x，cn201710647236.8)，该齿形改善了柔轮齿根的应 力状况和传动的啮合质量，提高承载能力和扭转刚度。双圆弧齿形设计常使用共轭法，如包 络法，瞬心法等，由已知的柔轮齿形，根据共轭理论，推导匹配的刚轮齿形。s形齿形(专 利号：美国专利us 3415143)，采用了齿条近似法，将柔轮齿形相对于刚轮分度圆的齿条近 似运动轨迹，按比例映射，同时得到柔轮和刚轮齿形。上述齿形及设计方法，存在一定的限 制，一是在齿形生成过程中，啮合范围难以调节，仅能在柔轮和刚轮齿形确定后计算得到； 且二是齿形啮合区间不连续，如双圆弧的两段圆弧之间会有5到10度的不连续区间；三是侧 隙较大，如渐开线齿侧隙一般为几十微米。啮合范围调节困难制约了谐波减速器的应用场景 和传动的承载能力；齿形啮合区间不连续，侧隙较大，制约了谐波减速器传动精度和稳定性。
3.随着对谐波减速器使用性能要求的提高，有必要设计出啮合范围调节更方便，啮合范围连续，侧隙小的齿形，从而让谐波减速器的应用场景更广泛，承载能力，传动精度和稳定性得到进一步提升。


技术实现要素：

4.发明目的：为了解决现有技术中存在的问题，本发明的目的是提出一种同时生成柔轮与刚轮齿形的谐波齿形设计方法，自动生成齿形曲线，啮合范围可调节，啮合连续且零侧隙的谐波齿形，有助于扩大谐波减速器的应用场景，提高谐波减速器的承载能力，传动精度和稳定性。
5.技术方案：为达到上述目的，本发明提供的技术方案为：
6.一种同时生成柔轮与刚轮齿形的谐波齿形设计方法，是基于柔轮弹性变形规律，步骤如下：
7.首先确定谐波减速器齿形设计所需的规格，模数，减速比和原始曲线方程等参数；
8.然后建立全局固定坐标系，柔轮和刚轮局部坐标系；
9.其次在全局坐标系中选择初始啮合位置，通过变换矩阵得到柔轮和刚轮局部坐标系中的相应坐标；根据柔轮变形规律，通过矩阵变换依次得到各啮合点；在确定啮合点数量，调节啮合范围后，同时得到柔轮和刚轮啮合曲线。
10.最后添加齿根曲线和过渡曲线，得到柔轮和刚轮完整齿形曲线。
11.具体来说，内容如下：
12.一种同时生成柔轮与刚轮齿形的谐波齿形设计方法，所述谐波齿形包括柔轮齿形和刚轮齿形，包括如下步骤：
13.(1)确定所设计谐波齿形的谐波减速器规格，模数m，减速比i以及原始曲线方程，即柔轮中性层曲线，推算柔轮齿数，刚轮齿数以及刚轮分度圆方程；
14.(2)建立全局固定坐标系，柔轮局部坐标系以及刚轮局部坐标系；
15.所述全局固定坐标系sw(ow；xw，yw)与波发生器固连，其中ow点为波发生器中心，xw轴与短轴重合，yw轴与长轴重合；
16.所述柔轮局部坐标系s
′f(o
′f；x
′f，y
′f)的o
′f点为柔轮中性层曲线等分点，x
′f轴与o
′f点的切向量重合，y
′f轴与o
′f点的法向量重合；具体的，将柔轮中性层曲线按弧长等分，等分数量nf为柔轮齿数zf的倍数；在柔轮中性层曲线的各等分点上依次建立柔轮局部坐标系，第i个等弧长位置坐标系为s
′
fi
(o
′
fi
；x
′
fi
，y
′
fi
)，o
′
fi
点位于第i个等分点上，x
′
fi
轴与该点的切向量重合，y
′
fi
轴与该点的法向量重合；
17.所述刚轮局部坐标系s
′c(o
′c；x
′c，y
′c)的o
′c点为刚轮分度圆等分点，x
′c轴与o
′c点的切向量重合，y
′c轴与o
′c点的法向量重合；具体的，将刚轮分度圆曲线按弧长等分，等分数量 nc为刚轮齿数zc的倍数；在各等分点上依次建立刚轮局部坐标系，第i个等弧长位置坐标系 s
′
ci
(o
′
ci
；x
′
ci
，y
′
ci
)，o
′
ci
点位于第i个等分点上，x
′
ci
轴与o
′
ci
点的切向量重合，y
′
ci
轴与o
′
ci
点的法向量重合；
18.(3)在全局固定坐标系中选择初始啮合位置，并通过变换矩阵得到柔轮局部坐标系和刚轮局部坐标系中的相应坐标；具体的，在全局固定坐标系sw中，选择初始啮合点，记为a1点，坐标为(x1,y1)；a1点在柔轮局部坐标系s
′
f1
中记为a
′
11
点，坐标为(x
′
f11
,y
′
f11
)，a
′
11
和a1点之间的关系式如下：
19.(x
′
f11
,y
′
f11
)＝m
wf11
(x1,y1)；
20.式中m
wf11
为sw到s
′
f1
的变换矩阵；
21.a1点在刚轮局部坐标系s
′
c1
中记为b
′
11
点，坐标为(x
′
c11
,y
′
c11
)；b
′
11
点和a1点之间的关系式如下：
22.(x
′
c11
,y
′
c11
)＝m
wc11
(x1,y1)；
23.式中m
wc11
为sw到s
′
c1
的变换矩阵；
24.(4)根据柔轮变形规律，通过矩阵变换依次得到各啮合点；
25.具体的，根据柔轮中性层曲线坐标上的点和对应的刚轮分度圆坐标上的点之间的运动关系，经坐标变换，由上一个啮合点在柔轮局部坐标系和刚轮局部坐标系同时各生成一个点，再将这两个点变换至全局固定坐标系，在这两个点之间取一个新的啮合点，依次推导各等分角度的啮合点；
26.(5)确定啮合点数量j，调节啮合范围εj，εj∈(0,1)，同时得到柔轮啮合曲线和刚轮啮合曲线；将啮合点拟合后，同时得到柔轮啮合曲线和刚轮啮合曲线；当i＝j时，在第i个啮
合点对应的柔轮坐标系s
′
fi
中，柔轮啮合弧长由点a
′
i,j
，a
′
i,j-1
…a′
i,2
，a
′
i,1
构成，将啮合点拟合后，作为柔轮的齿形曲线；其中a
′
i,j-1
对应第i个啮合点，由s
′
fi-1
坐标中的a
′
i-1,j-1
坐标变化得到；同时，在对应的刚轮坐标系s
′
ci
中，刚轮啮合弧长由点b
′
i,j
，b
′
i,j-1
…b′
i,2
，b
′
i,1
构成，将啮合点拟合后，作为刚轮的齿形曲线；其中b
′
i,j-1
对应第i个啮合点，由s
′
ci-1
坐标中的b
′
i-1,j-1
坐标变化得到；
27.(6)添加齿根曲线和齿顶和齿根过渡曲线，得到完整的柔轮齿形曲线和刚轮齿形曲线；具体步骤是：将步骤(5)中拟合得到的柔轮啮合曲线和刚轮啮合曲线作为齿顶曲线，添加齿根曲线，所述齿根曲线为任意光滑曲线，但需要满足与刚轮齿廓不干涉的条件；添加齿顶和齿根过渡圆弧曲线后，得到柔轮完整齿形曲线和刚轮完整齿形曲线
28.上述同时生成柔轮与刚轮齿形的谐波齿形设计方法，在全局固定坐标系sw(ow；xw，yw) 中，原始曲线为椭圆，方程如下：
29.椭圆方程：
30.其中a为椭圆长半轴，b为椭圆短半轴。
31.上述同时生成柔轮与刚轮齿形的谐波齿形设计方法，在全局固定坐标系sw(ow；xw，yw) 中，原始曲线为余弦曲线，方程如下：
32.余弦曲线方程：
33.其中ρ为柔轮变形后中性层极半径，rf为柔轮变形前中性层半径，ω0为柔轮半轴最大变形量，为柔轮转角。
34.上述同时生成柔轮与刚轮齿形的谐波齿形设计方法，齿厚由初始啮合点a1的横坐标x1决定，其取值满足约等式x1≈π/4
·
m，其中m为模数。
35.所述初始啮合点a1的纵坐标y1选在刚轮分度圆半径rc附近，满足|r
c-y1|＜0.15mm。
36.上述同时生成柔轮与刚轮齿形的谐波齿形设计方法，步骤(4)中，由初始啮合点推导第 2个啮合点的具体过程如下：
37.将a
′
11
点由柔轮局部坐标系s
′
f1
变换到柔轮局部坐标系s
′
f2
中，记为a
′
21
点，坐标为(x
′
f21
, y
′
f21
)，如式所示：
38.(x
′
f21
,y
′
f21
)＝m
ff21
(x
′
f11
,y
′
f11
)；
39.式中m
ff21
为s
′
f1
到s
′
f2
的变换矩阵；
40.a
′
21
点在sw中记为a
21
点，坐标为(x
f21
,y
f21
)，a
21
点和a
′
21
点之间的关系式如下：
41.(x
f21
,y
f21
)＝m
′
ff21
(x
′
f21
,y
′
f21
)；
42.式中m
′
ff21
为s
′
f1
到sw的变换矩阵；
43.然后，将b
′
11
点由刚轮局部坐标系s
′
c1
变换到刚轮局部坐标系s
′
c2
中，记为b
′
21
点，坐标为(x
′
c21
,y
′
c21
)；b
′
21
点在sw中记为b
21
点，坐标为(x
c21
,y
c21
)；
44.在a
21
和b
21
两点连线上或连线附近区域选取第二个啮合点，在sw中记为a2点，坐标为 (x2,y2)；a2点和a
21
和b
21
两点的位置关系式如下：
45.(x2,y2)＝[k
x1
(x
f21
+x
c21
),k
y1
(y
f21
+y
c21
)]；
[0046]
其中，k
x1
,k
y1
为比例系数，k
x1
,k
y1
∈(0,1)；
[0047]
则a2点的坐标为：
[0048][0049]
上述同时生成柔轮与刚轮齿形的谐波齿形设计方法，步骤(4)中，第i个啮合点由第i-1 个啮合点推导得到：
[0050][0051]
各啮合点的坐标为：
[0052][0053]
其中，k
x1
，k
x2
…kx(i-1)
,k
y1
，k
y2
…ky(i-1)
为比例系数，取值区间为(0,1)，m
wfii
为坐标系sw到坐标系s
′
fi
的变换矩阵，m
wcii
为坐标系sw到s
′
ci
的变换矩阵，m
ffi+1,i
为坐标系s
′
fi
到s
′
fi+1
的变换矩阵，m
′
ffi+1,i
为坐标系s
′
fi+1
到sw的变换矩阵，m
cci+1,i
为坐标系s
′
ci
到s
′
ci+1
的变换矩阵， m
′
cci+1,i
为坐标系s
′
ci+1
到sw的变换矩阵。
[0054]
上述同时生成柔轮与刚轮齿形的谐波齿形设计方法，啮合点的取值数量决定了啮合范围，通过改变啮合点数量j以调节啮合范围εj，j＝εj·
nf，nf为柔轮中性层曲线等分数量；当nf为定值时，啮合点数量j越多，接触弧长越长，啮合范围越大，重合度越高。
[0055]
上述同时生成柔轮与刚轮齿形的谐波齿形设计方法，：原始曲线长半轴的最大径向变形量满足不等式|ω
0-m|＜0.1mm，其中ω0为柔轮长轴最大变形量，m为模数。
[0056]
上述同时生成柔轮与刚轮齿形的谐波齿形设计方法，柔轮中性层曲线长半轴a和刚轮分度圆半径rc满足不等式4
.
m＞r
c-a＞0。
[0057]
有益效果：本发明基于柔轮弹性变形规律，提供了一种新的谐波齿形设计方法，得到的齿形，具有啮合范围调节方便，啮合范围连续，侧隙小的特点。相较于传统的谐波齿形设计方法，本发明应用场景更广阔，可以显著提高谐波减速器传动过程的承载能力，传动精度和稳定性。
附图说明
[0058]
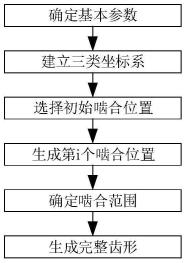
图1为本发明的齿形设计总流程图；
[0059]
图2为本发明实施例1的三类坐标示意图；
[0060]
图3为本发明实施例1的第i个啮合点推导流程图；
[0061]
图4为本发明实施例1的柔轮齿形图；
[0062]
图5为本发明实施例1的刚轮齿形图；
[0063]
图6为本发明实施例1的谐波齿轮第一象限啮合状态图；
[0064]
图7为本发明实施例1的啮合范围图；
[0065]
图8为本发明实施例1的侧隙分布图。
具体实施方式
[0066]
下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其它实施例，都属于本发明保护的范围。
[0067]
除非另有定义，本文所使用的所有的技术和科学术语与属于本发明的技术领域的技术人员通常理解的含义相同；本文中在本发明的说明书中所使用的术语只是为了描述具体的实施例的目的，不是旨在于限制本发明；本文所使用的术语“及/或”包括一个或多个相关的所列项目的任意的和所有的组合。
[0068]
实施例1
[0069]
一种同时生成柔轮与刚轮齿形的谐波齿形设计方法，根据特定谐波减速器的规格(本实施例中采用40型、减速比为100、模数0.508mm)，主要应用在为机器人末端执行机构中，啮合范围要求大于30％。利用椭圆型凸轮波发生器，确定啮合范围，同时得到柔轮和刚轮的参与啮合部分齿形，进而得到完整齿形，整体设计流程如图1所示。具体步骤如下：
[0070]
步骤1：确定基本参数
[0071]
谐波减速器型号40，减速比为100、模数0.508mm，柔轮齿数zf＝200，刚轮齿数zc＝202，柔轮分度圆rf＝50.8mm，刚轮分度圆rc＝51.308mm。
[0072]
在固定坐标系sw中，柔轮原始曲线(即中性层变形曲线)为标准椭圆，方程为：
[0073][0074]
本实施例中，原始曲线长轴a＝49.808mm，原始曲线短轴b＝48.673mm。
[0075]
初始啮合点x1＝0.41mm，初始啮合点y1＝51.408mm。
[0076]
长轴径向变形量ω＝0.566。
[0077]
比例系数k
x1
,k
y1
均取0.5。啮合范围设定为33％，即共有68对齿同时参与啮合。
[0078]
步骤2：建立三类坐标系，分别是全局固定坐标系，柔轮和刚轮局部坐标系。如图2所示，图中1为全局固定坐标系sw，2为柔轮坐标系s
′
fi
，3为刚轮坐标系s
′
ci
，4为刚轮分度圆曲线，5为柔轮原始曲线。
[0079]
全局固定坐标系sw(ow；xw，yw)与波发生器固连，ow点为波发生器中心，xw轴与短轴重合，yw轴与长轴重合。
[0080]
柔轮局部坐标系s
′f(o
′f；x
′f，y
′f)，o
′f位于柔轮中性层曲线等分点，x
′f轴与该点的切向量重合，y
′f轴与该点的法向量重合。将柔轮中性层曲线按弧长等分，等分数量nf为200。在各等分点上依次建立坐标系，如第i个等弧长位置坐标系s
′
fi
(o
′
fi
；x
′
fi
，y
′
fi
)，o
′
fi
点位于第i 个等分点上，x
′
fi
轴与该点的切向量重合，y
′
fi
轴与该点的法向量重合。
[0081]
刚轮局部坐标系s
′c(o
′c；x
′c，y
′c)，o
′c位于柔轮分度圆等分点，x
′c轴与该点的切向量重合，y
′c轴与该点的法向量重合。将刚轮分度圆曲线按弧长等分，等分数量nc为202。在各等分点上依次建立坐标系，如第i个等弧长位置坐标系s
′
ci
(o
′
ci
；x
′
ci
，y
′
ci
)，o
′
ci
点位于第i个等分点上，x
′
ci
轴与该点的切向量重合，y
′
ci
轴与该点的法向量重合。
[0082]
步骤3：在全局坐标系中选择初始啮合位置，并通过变换矩阵得到柔轮和刚轮局部坐标系中的相应坐标。本例中，在固定坐标系sw中，初始啮合点a1点，坐标为(x1,y1)，x1＝
0.41mm， y1＝51.408mm。在刚轮坐标系s
′
c1
中记为b
′
11
点，坐标为(x
′
c11
,y
′
c11
)。a
′
11
和a1点之间的关系如式：
[0083]
(x
′
f 11
,y
′
f 11
)＝m
wf11
(x1,y1)，
[0084]
式中m
wf11
为sw到s
′
f 1
的变换矩阵。
[0085]b′
11
点和a1点之间的关系如式：
[0086]
(x
′
c11
,y
′
c11
)＝m
wc11
(x1,y1)，
[0087]
式中m
wc11
为sw到s
′
c1
的变换矩阵。
[0088]
步骤4：根据柔轮变形规律，通过矩阵变换依次得到各啮合点。
[0089]
将a
11
点由柔轮坐标系s
′
f 1
变换到柔轮坐标系s
′
f 2
中，记为a
′
21
点，坐标为(x
′
f 21
,y
′
f 21
)，如式所示：
[0090]
(x
′
f21
,y
′
f21
)＝m
ff21
(x
′
f11
,y
′
f11
)，
[0091]
式中m
ff21
为坐标系s
′
f1
到s
′
f2
的变换矩阵。
[0092]a′
21
点在sw中记为a
21
点，坐标为(x
f21
,y
f21
)，a
21
点和a
′
21
点之间的关系如式所示，
[0093]
(x
f21
,y
f21
)＝m
′
ff21
(x
′
f21
,y
′
f21
)，
[0094]
式中m
′
ff21
为坐标系s
′
f1
到sw的变换矩阵。
[0095]
然后，将b
11
点由刚轮坐标系s
′
c1
变换到s
′
c2
中，记为b
′
21
点，坐标为(x
′
c21
,y
′
c21
)。b
′
21
点在sw中记为b
21
点，坐标为(x
c21
,y
c21
)。
[0096]
在a
21
和b
21
两点连线上选取第二个啮合点，在sw中记为a2点，坐标为(x2,y2)。a2点和 a
21
和b
21
两点的位置关系如式：
[0097]
(x2,y2)＝(k
x1
(x
f21
+x
c21
),k
y1
(y
f21
+y
c21
))，
[0098]
其中，k
x1
,k
y1
为比例系数，k
x1
,k
y1
∈(0,1)，本例中，比例系数k
x1
,k
y1
均取0.5。
[0099]
则a2点的坐标为：
[0100][0101]
本实施例中，x2＝0.41mm，y2＝51.409mm。
[0102]
第i个啮合点，其可由第i-1个啮合点推导，流程图如图3所示：
[0103][0104]
第i个啮合点的坐标为：
[0105][0106]
步骤5：确定啮合点数量j，调节啮合范围εj，同时得到柔轮和刚轮啮合曲线。啮合点数量取值越大，啮合范围越大，但啮合范围过大易造成干涉。本实施例中第一象限啮合点
数j 为34，啮合范围εj设定为33％。将34个啮合点转换至同一个柔轮坐标系中，本实施例中，先将各点变化至柔轮坐标系s
′
f1
和刚轮坐标系s
′
c1
，再转化至全局固定坐标系sw中，即可得到柔轮和刚轮的啮合点坐标：
[0107]
表1柔轮和刚轮啮合点坐标
[0108][0109][0110]
在全局固定坐标系sw中，拟合柔轮和刚轮啮合点。
[0111]
步骤6：添加齿根曲线和过渡曲线，得到柔轮和刚轮完整齿形曲线和将步骤
(5)中拟合得到的柔轮和刚轮啮合曲线作为齿顶曲线，添加齿根曲线，齿根曲线可采用光滑曲线，满足不干涉条件即可。添加齿顶和齿根过渡圆弧曲线后，即得到了完整的柔轮齿形和刚轮齿形如图4，5所示，由齿顶曲线，齿根曲线和齿顶和齿根过渡圆弧曲线四部分组成。
[0112]
本实施例中，柔轮总齿数为200，通过设定固定坐标系第一象限啮合点数j为34，调节啮合范围为33％，实际啮合范围为32.77％，重合度为65.54，第一象限啮合状态范围如图6 所示，图中1为柔轮，2为刚轮。3为0度位置，此时柔轮与刚轮完全啮合；4为59.44度位置，此时柔轮刚啮出；5为90度位置，此时柔轮与刚轮完全脱开，验证了本设计方法具有啮合范围调节方便的特点。齿形在整个啮合范围[0.46
°
,59.44
°
]内，柔轮和刚轮啮合连续，柔轮的啮合弧长和角度的对应关系如图7所示，验证了本设计方法设计的齿形具啮合范围连续的特点。在啮合区间，侧隙在0.46
°
到59.44
°
范围内稳定在5
×
10-3
μm，如图8所示，相比于渐开线齿侧隙一般为几十微米，啮合侧隙分布更均匀，最大啮合侧隙更小，验证了本设计方法设计的齿形具有侧隙小的特点。
[0113]
实施例2
[0114]
谐波减速器型号40，减速比为100、模数0.508mm，柔轮齿数zf＝200，刚轮齿数zc＝202，柔轮分度圆rf＝50.8mm，刚轮分度圆rc＝51.308mm。
[0115]
在固定坐标系sw中，柔轮原始曲线(即中性层变形曲线)为余弦曲线，方程为：
[0116][0117]
本实施例中，rf＝50.8mm，ω0＝0.566mm。
[0118]
初始啮合点x1＝0.41mm，初始啮合点y1＝51.408mm。
[0119]
比例系数k
x1
,k
y1
均取0.5。啮合范围设定为33％，即共有68对齿同时参与啮合。
[0120]
与实施例1采用相同步骤，可得到柔轮和刚轮的啮合点坐标：
[0121]
表2柔轮和刚轮啮合点坐标
[0122][0123]
进而拟合得到柔轮和刚轮的齿顶曲线，添加齿根曲线和齿顶和齿根过渡曲线，得到柔轮和刚轮完整齿形曲线。
[0124]
以上所述实施例仅表达了本发明的某种实施方式，其描述较为具体和详细，但并不能因此而理解为对本发明专利范围的限制；应当指出的是，对于本领域的普通技术人员来说，在不脱离本发明构思的前提下，还可以做出若干变形和改进，这些都属于本发明的保护范围。