一种定形相变材料相变函数测量方法与流程

本发明属于热物性参数测量方法领域，具体涉及一种定形相变材料相变函数测量方法。

背景技术：
能源危机以来，相变储能的基础和应用研究成为热门课题。相变材料不仅可以储存能量，还可以减小温度波动，起到移峰填谷的作用，然而传统的固-液相变材料在使用中要考虑到密封问题和传热效率低等问题。定形相变材料因其工作物质发生相变时保持形状不变，不泄漏，载体基质可以提高导热性能等优良特性有着广阔的应用前景。定形相变材料的相变点、热容、潜热、导热系数等热物性参数是评价其性能好坏的重要指标。测量相变材料热容、潜热的方法主要有绝热量热法、差示扫描量热法（DSC），差热分析法（DTA）。绝热量热法虽然测量准确度高，但其测量过程十分复杂。差示扫描量热法（DSC），差热分析法（DTA）测量样品量过小（5-10mg）,对不均匀的材料测量误差较大，应用于工程材料的热容、潜热测量并不适合。这些测量方法还有一些共同的缺点，即装置复杂昂贵，不能同时测定导热系数。近年来不少学者意识到现有测量方法的不足，提出了几种改进的测量方法，其中比较有代表性的有我国学者张寅平提出的温变曲线分析法（Yinping,Z.;Yi,J.,Asimplemethod,theT-historymethod,ofdeterminingtheheatOffusion.specificheatandthermalconductivityofphase-changematerials.MeasSeiTechnoL1999,10.）和法国学者提出的正则化方法（PalomoDelBarrio,E.;Dauvergne,J.L.;Morisson,V.,Asimpleexperimentalmethodforthermalcharacterizationofshape-stabilizedphasechangematerials.JournalofSolarEnergyEngineering2009,131(4).）。前者仅利用相变材料和参比物水的温降曲线即可测定相变材料凝固点、比热、潜热、导热系数，并用该方法测量了一些水合盐、脂酸、石蜡和自研相变材料水合盐类的热物性，测试结果与文献值较为符合，但这种方法不适用于定形相变材料。后者则设计了一种简单的定形相变材料热物性参数测量方法，通过求解正则化算子得到相变函数。数学理论抽象，处理过程复杂，自2009年提出至今还未见其他研究者进行重复或类似实验。

技术实现要素：
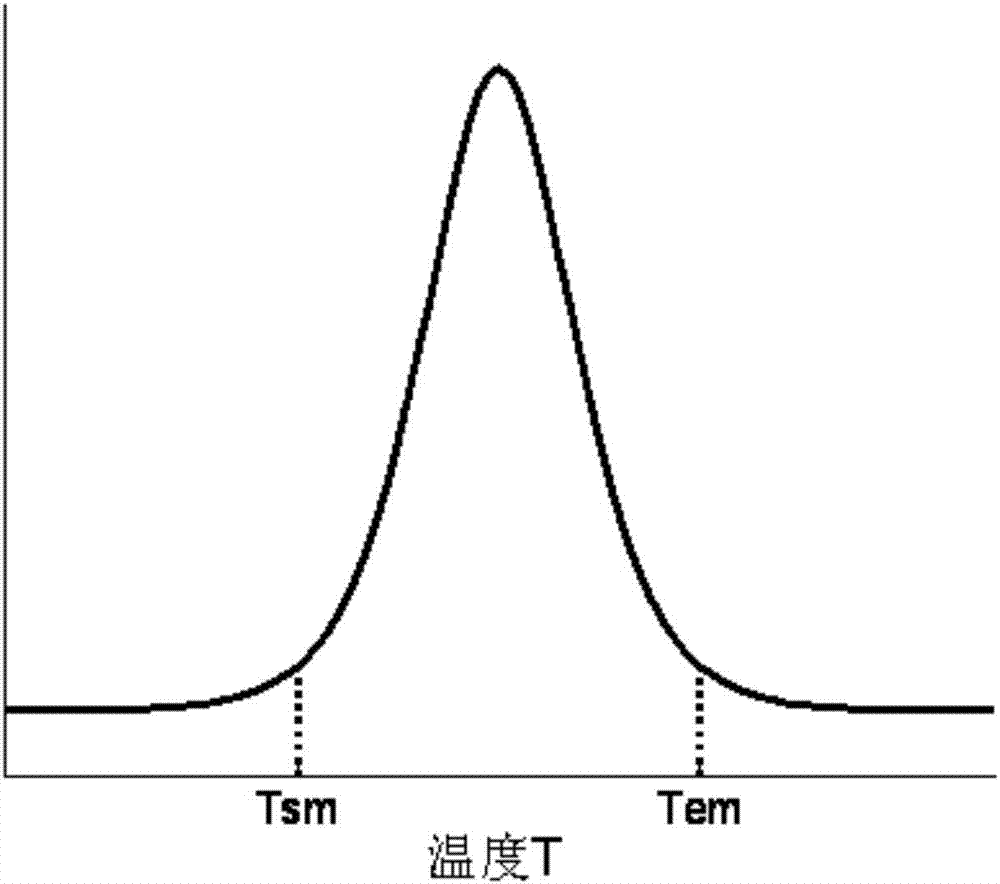
本发明的目的在于克服上述缺点，提供一种定形相变材料相变函数测量方法。为达到上述目的，本发明采取的技术方案包括以下步骤：1）将已知导热系数的粉末状的标准物质放入两端为绝热条件的金属管中，金属管内部的同一横截面上设有第一、第二、第三热电偶，第一、第二、第三热电偶埋在标准物质中，第一、第二、第三热电偶与圆心的距离分别为r1、r2和r3，且r1<r2<r3，金属管的内壁上设有第四热电偶、金属管的外壁上设有第五热电偶；2）室温下，采集第一、第二、第三、第四、第五热电偶的温度数据，待采集的温度数据均稳定后，将金属管加热至60-200℃并同时采集加热过程中的第一、第二、第三、第四、第五热电偶的温度数据，得到标准物质的第一、第二、第三、第四、第五热电偶的温度随时间的变化曲线，利用式[9]求出金属管的管壁的导热系数λw，其中：Std为被测量物质的第四、第五热电偶的温度随时间的变化曲线的积分面积差，l是被测量物质的长度，λ是被测量物质的导热系数，V是被测量物质的体积，dout是金属管外径，din是金属管内径，Spc为函数G(T)/λ的积分面积，t为时间，T为温度，T1、T2和T3分别为第一、第二、第三热电偶测得的温度，H为单位体积焓；3）将待测的定形相变材料放入金属管中，使第一、第二、第三热电偶埋在定形相变材料中，室温下，采集第一、第二、第三、第四、第五热电偶的温度数据，待采集的温度数据均稳定后，将金属管加热至设定温度，设定温度比定形相变材料的相变温度上限高10-20℃，同时采集加热过程中的第一、第二、第三、第四、第五热电偶的温度数据，待采集的温度数据均再次稳定后继续测量10-30min，然后将金属管降至室温并同时采集降温过程中的第一、第二、第三、第四、第五热电偶的温度数据，得到定形相变材料的第一、第二、第三、第四、第五热电偶的温度随时间的变化曲线，再利用式[9]求出定形相变材料的导热系数λ；4）利用和式[5]，求出定形相变材料的相变前比热cs，相变后比热cl和相变潜热L，其中：Tsm,Tem分别为定形相变材料的相变起始温度和相变结束温度，ρs，ρl分别为定形相变材料的相变前密度和相变后密度。所述的标准物质为α-Al2O3。所述的第一、第二、第三、第四、第五热电偶位于同一条直线上。相对于现有技术，本发明具有以下有益效果：1.测量对象方面，本发明提供的测量方法只需对待测物质进行一次升温过程的测量就能得到该物质的热物性参数，包括固态比热，液态比热，相变潜热，相变函数和导热系数。与复杂、昂贵的DSC相比，本发明的测量方法所使用的装置简单，方便携带，并且在混合物的测量中更有优势，因为DSC取样量非常少（5-10mg），如果混合不均匀，会造成极大的误差，同时由于DSC取样量少，会加剧测量过程中的过热、过冷现象，导致测得的热物性参数存在一定的偏差，而本发明的测量方法所使用的装置的取样量远远大于DSC的取样量，能够很好的避免测量时出现的误差。2.在理论推导方面，本发明提供的测量方法通过对热传导方程的巧妙求解，对每种情况进行了物理分析，从而得到式[5]，并且在推导过程中，对实际的函数赋以相变函数G(T)的物理意义。运用传入金属管能量等于定形相变材料吸收的能量得到式[9]，从而定量的求出被测量物质的导热系数。本发明提供的测量方法，无论是对程序中的数值处理，还是理论上推导研究，都有着重要的意义。3.对于实验装置方面，本发明的测量方法所使用的装置中用金属管作为量热容器，金属管上下底绝热，升温时对金属管进行均匀加热，使得数据处理时的边界条件变得十分简单，只需径向的数据处理，不仅减小测量点的数量，而且降低了后期数据处理的难度，提高了后期数据处理的精准度。4.用标准物质确定金属管导热系数时，运用标准物质可以将热电偶与金属管壁面的接触热阻，以及金属管表面腐蚀等因素对导热能力的影响包含在求得的导热系数中，使得测量得到的结果更加真实准确。附图说明图1为液相体积分数（f函数）随温度变化的示意图；图2为Delta函数（δ(T)）随温度变化的示意图；图3为升温段内外壁温度随时间变化的示意图，其中a为外壁温度随时间的变化曲线，b为内壁温度随时间的变化曲线，c为温差面积；图4为未定标相变函数的示意图；图5为升温阶段温变曲线，其中a为第五热电偶的温度曲线，b为第四热电偶的温度曲线，c为第三热电偶的温度曲线，d为第二热电偶的温度曲线，e为第一热电偶的温度曲线；图6为升温阶段相变函数图。图7为降温阶段温变曲线，其中a为第五热电偶的温度曲线，b为第四热电偶的温度曲线，c为第三热电偶的温度曲线，d为第二热电偶的温度曲线，e为第一热电偶的温度曲线；（图7中b、c曲线重叠了）图8为降温阶段相变函数图。具体实施方式下面结合附图和具体实施例对本发明作进一步的详细说明。本发明提供的测量方法的思路为：在实验中先用标准物质确定λw的数值，再对定形相变材料进行测量，并运用[9]式算出定形相变材料导热系数λ，进而定标得到物质实际的相变图。再运用式[5]可以就算出相变前比热cs，相变后比热cl，相变潜热L。这样仅通过一次升温和降温过程就能测量得到相变物质各热物性参数。将采集到的温度信号按照本发明提供的测量方法的理论部分阐述的过程进行数值计算，得到如图6的相变函数图，相变函数图中尖峰两侧拐点作为相变起始温度和相变结束温度,相变起始温度前和相变结束温度后相变函数的平均值就分别为相变前比热cs，相变后比热cl，从而由[5]式得到相变潜热L。本发明提出的定形相变材料相变函数测量方法，包括以下步骤：1）将已知导热系数的粉末状的标准物质α-Al2O3放入两端为绝热条件的金属管中，金属管内部的同一横截面上设有第一、第二、第三热电偶，第一、第二、第三热电偶埋在α-Al2O3中，第一、第二、第三热电偶与圆心的距离分别为r1、r2和r3，且r1<r2<r3，金属管的内壁上设有第四热电偶、金属管的外壁上设有第五热电偶；第一、第二、第三、第四、第五热电偶位于同一条直线上；2）室温下，采集第一、第二、第三、第四、第五热电偶的温度数据，待采集的温度数据均稳定后，将金属管加热至60-200℃并同时采集加热过程中的第一、第二、第三、第四、第五热电偶的温度数据，得到标准物质的第一、第二、第三、第四、第五热电偶的温度随时间的变化曲线，利用式[9]求出金属管的管壁的导热系数λw，其中：Std为被测量物质的第四、第五热电偶的温度随时间的变化曲线的积分面积差，l是被测量物质的长度，λ是被测量物质的导热系数，V是被测量物质的体积，dout是金属管外径，din是金属管内径，Spc为函数G(T)/λ的积分面积，t为时间，H为单位体积焓，T为温度，为温度对空间的二阶微分，由第一、第二、第三热电偶的测量的数值差分得到，由于对角度方向的偏导为0，故T1、T2和T3分别为第一、第二、第三热电偶测得的温度；3）将待测的定形相变材料放入金属管中，使第一、第二、第三热电偶埋在定形相变材料中，室温下，采集第一、第二、第三、第四、第五热电偶的温度数据，待采集的温度数据均稳定后，将金属管加热至设定温度，设定温度比定形相变材料的相变温度上限高10-20℃，同时采集加热过程中的第一、第二、第三、第四、第五热电偶的温度数据，待采集的温度数据均再次稳定后继续测量10-30min，然后将金属管降至室温并同时采集降温过程中的第一、第二、第三、第四、第五热电偶的温度数据，得到定形相变材料的第一、第二、第三、第四、第五热电偶的温度随时间的变化曲线，再利用式[9]求出定形相变材料的导热系数λ；4）利用和式[5]，求出定形相变材料的相变前比热cs，相变后比热cl和相变潜热L，其中：T为温度，Tsm,Tem分别为定形相变材料的相变起始温度和相变结束温度，ρs，ρl分别为定形相变材料的相变前密度和相变后密度，t为时间，H为单位体积焓，为温度对空间的二阶微分，由第一、第二、第三热电偶的测量的数值差分得到。本发明提供的测量方法的理论如下：只有径向导热的圆柱体相变热传导方程为其中H是单位体积焓；t代表时间；λ是被测量物质导热系数；T是该点处温度；而单位体积焓H能够写成H(t)=[ρscs(1-f(t))+ρlclf(t)]T(t)+ρlLf(t)[2]其中ρs,ρl分别为被测量物质的相变前密度和相变后密度；cs,cl分别为被测量物质的相变前比热和相变后比热；f是被测量物质的液相的体积分数（单位体积的被测量物质中液态所占比例），是t的函数，也可以写成是T的函数；L是被测量物质的相变潜热。将[2]式代入到[1]式中，并令温度T作为自变量，得到[3]式根据求导链式法则，并记Δ(ρc)=ρlcl-ρscs，得到记方程右边为这一函数由第一、第二、第三热电偶温度数据结合热电偶位置数据差分得到。f(T),δ(T)示意图分别如图1，图2所示,Tsm,Tem分别为被测量物质的相变起始温度和相变结束温度。液相的体积分数f是温度T的函数，相变发生至相变结束过程中，f由0变为1；δ(T)是f对温度的导数，其变化过程如图2所示，其中的尖峰即为被测量物质的相变过程。对[4]式左边进行积分可得：实验所测的是温度的时间序列T=T(t)，如果只用升温段数据得到图3内外壁温度随时间变化图，其中a是第五热电偶测得的金属管外壁温度随时间变化曲线，b是第四热电偶测得的金属管内壁温度随时间变化曲线，由a、b围成的c即为温差面积Std。而对于研究点可以结合第一、第二、第三热电偶测得的被测量物质距圆心不同距离处的温度随时间变化数据运用差分法算出可以得到即图4未定标相变图，图4中的曲线为G(T)/λ，曲线与横坐标围成的面积为相变面积Spc。根据傅里叶导热定律得到传入的能量为：其中Qin是整个过程外界传入能量，λw是金属管的管壁的导热系数，l是被测量物质长度，dout是金属管外径，din是金属管内径,Tin是金属管内壁温度，Tout是金属管外壁温度，Std是第四、第五热电偶的温度随时间的变化曲线的积分面积差，即温差面积（如图3所示）。吸收的能量，借助G(T)的定义得知：其中Qab是定形相变材料吸收的能量，V是定形相变材料的体积，λ是定形相变材料的导热系数，Spc是函数G(T)/λ曲线的积分面积，即图4中曲线与横轴的积分面积，是相变面积。又根据进入金属管内热量等于定形相变材料吸收的能量：Qin=Qab[8]将[6]，[7]两式代入[8]式得到从而可以对图4相变图进行定标。下面以月桂酸/膨胀石墨复合材料的热容和相变潜热的测量为例来说明本发明的方法测量的准确性。此时视为金属管的导热系数λw已按权利要求1所述步骤1），2）由标准物质得到。月桂酸/膨胀石墨复合材料的制备方法为：第一步向坩埚中加入可膨胀石墨，放入马弗炉中，升温至400℃，维持一分钟，停止加热，倒入广口瓶备用；第二步混合月桂酸和膨胀石墨，按照1：5的质量比称量适量月桂酸和烧结过的膨胀石墨，倒入烧杯，用薄膜覆盖烧杯口，在70-80℃下水浴加热。将待测的月桂酸/膨胀石墨复合材料放入金属管中，金属管内部的同一横截面上设有第一、第二、第三热电偶，第一、第二、第三热电偶埋在月桂酸/膨胀石墨复合材料中，第一、第二、第三热电偶分别位于距圆心处6mm(r1)，12mm(r2)，17mm(r3)处，金属管的内壁上设有第四热电偶、金属管的外壁上设有第五热电偶，共五个测点，第一、第二、第三、第四、第五热电偶位于同一条直线上。室温下，用数据采集器采集第一、第二、第三、第四、第五热电偶的温度数据，待数据采集器测得的温度数据均稳定后，将温度升至设定温度（55℃），设定温度比月桂酸/膨胀石墨复合材料相变温度上限（45℃）高10℃，同时采集加热过程中的第一、第二、第三、第四、第五热电偶的温度数据，待采集的温度数据均再次稳定后继续测量20min，然后将金属管降至室温。加热和冷却过程中用数据采集器采集第一、第二、第三、第四、第五热电偶的温度数据，做出复合材料的第一、第二、第三、第四、第五热电偶的温度随时间的变化曲线，升温段的各测点温度随时间变化的曲线如图5所示，降温段的各测点温度随时间变化的曲线如图7所示。以升温段的数据处理为例，根据理论部分处理相变曲线的办法，选取12mm的点作为研究对象，对12mm的曲线（图5中的d曲线）进行数值时间微分并运用17mm和6mm的曲线（分别为图5中的c曲线和e曲线）得到12mm点的温度对空间二阶微分项，处理得到未定标的相变曲线图，即G(T)/λ图。在定标过程，先用金属管内壁、金属管外壁温度随时间变化数据（分别为图5中的b曲线和a曲线）结合[6]式得到吸收热量Qin，运用[9]式，得到月桂酸/膨胀石墨复合材料导热系数λ，代入各G(T)处，处理得相变曲线定标后的值。最终得到定标后升温段的月桂酸/膨胀石墨复合材料相变曲线（图6）。同理，将图7中的数据处理后能够得到降温段的月桂酸/膨胀石墨复合材料相变曲线（图8）。得到相变曲线后，根据理论[5]式推导得到的结论，在相变温度前可以得到相变前热容，同理通过相变温度后的曲线数值得到相变后热容。相变过程的潜热，可以对G(T)函数积分得到。最终得到相变物质的热物性参数如表1所示。表1.月桂酸/膨胀石墨复合材料热物性参数从表1中可以看出本方法处理出来的数据，与常用测试方法DSC所得结果相比，本发明的误差在可以接受的范围内，同时本发明所用的装置在结构复杂程度，大小，成本方面优于DSC方法。