一种基于参数辨识的机载分布式POS传递对准方法与流程

本发明涉及一种基于参数辨识的机载分布式POS传递对准方法，可用于各种需要通过传递对准技术来确定位置、速度和姿态的捷联惯性导航系统，特别适合于机体存在弹性变形的情况。

背景技术：
多任务遥感载荷是目前机载对地观测发展方向之一，如集成高分辨率测绘相机、成像光谱仪、大视场红外扫描仪、合成孔径雷达(SyntheticApertureRadar，SAR)于同一载机的多任务载荷，机载分布式阵列天线SAR和柔性多基线干涉SAR等。对于装备任务遥感载荷的高性能航空遥感系统，需要对各载荷分布点的运动参数实现高精度测量。位置姿态测量系统(PositionandOrientationSystem，POS)是目前机载对地观测遥感载荷获取位置、速度、姿态等运动参数的主要手段，其主要组成包括IMU、全球定位系统、导航计算机和后处理软件。对于装备了多个或多种观测载荷的高性能综合机载对地观测系统，由于多个或多种观测载荷安装在飞机的不同位置，飞机弹性变形导致载荷间的空间相对关系发生变化。此时，传统的单一POS显然无法满足不同安置点多载荷的高精度运动参数测量的需求。因此，必须建立起高精度分布式时空基准系统(机载分布式POS系统)为高性能综合机载对地观测系统中所有载荷提供高精度的时间、空间信息，其典型的应用载荷为分布式阵列天线SAR。分布式SAR天线分布在机翼两侧，需要对各天线处的位置、速度、姿态以及主、子系统基线进行高精度测量。机载分布式POS系统一般由一个高精度主POS和多个子惯性测量单元(InertialMeasurmentUnit，IMU)组成。主POS一般安装在载机机舱内；子IMU一般分布安装在机体的不同位置(包括机翼)，依靠主POS的高精度位置、速度、姿态等运动参数对其进行传递对准以实现所在处运动信息的精确测量。由于飞机机体存在弹性变形，主子系统间除了确定性的杆臂误差和安装误差角以外，还存在随时间变化的随机杆臂误差和弹性变形角。其中随时间变化的随机杆臂误差和弹性变形角，不仅无法精确测量，而且会在主、子系统传递对准中引入复杂的随机误差，从而使子IMU运动参数测量精度下降。因此，需要在传递对准过程中对飞机的弹性变形进行估计和补偿。实际飞行中的弹性变形有两种，一种是由于载机机动所产生的挠曲变形，另一种是载机内部振源或阵风等使载机产生的振动变形，这两种变形一般都可以看作是随机过程。现有的对弹性变形角进行补偿的方法主要有三种：第一种方法是利用软件模拟机体弹性运动模型，例如公开号为201210113395的专利采用ANSYS辅助建模的方法模拟机翼弹性变形，但该方法所建立的模型随飞机材质的变化而变化，并且没有考虑外挂载荷对飞机弹性变形的影响。第二种方法是采用加大卡尔曼滤波器过程噪声矩阵来减小机体变形和振动的影响。该方法是依据真实模型的协方差分析结果来确定注入白噪声的强度，即通过加大过程噪声来补偿建模的挠曲变形。该方法除了可以补偿挠曲运动外，还可以增加滤波器的鲁棒性，但是以降低传递对准的精度为代价的(KainJ.E.,CloutierJ.R..Rapidtransferalignmentfortacticalweaponapplications[C].AIAAGuidance,NavigationandControlConference.1989:1290-1300.)。第三种方法是经验建模方法，也是较为常用的方法，即将机体弹性变形角理想化为二阶或三阶的马尔科夫过程，并将其增广为卡尔曼滤波的状态变量，通过卡尔曼滤波估计出该弹性变形角并进行补偿(李端昌,钟麦英,郭丁飞.分布式POS传递对准中的误差检测与补偿[C].第25届中国控制与决策会议论文集.2013:4194-4199.)。但该方法存在的问题是上述参数的选择多凭经验确定，在实际工程应用中难以保证该参数的准确性。此外，机体弹性变形角的马尔科夫过程参数在飞机飞行过程中会随外界因素发生改变，即使在滤波开始阶段能够根据经验给出相应的过程参数，也不能保证系统状态模型和噪声统计特性在滤波过程中的准确性，滤波精度将下降甚至出现发散。

技术实现要素：
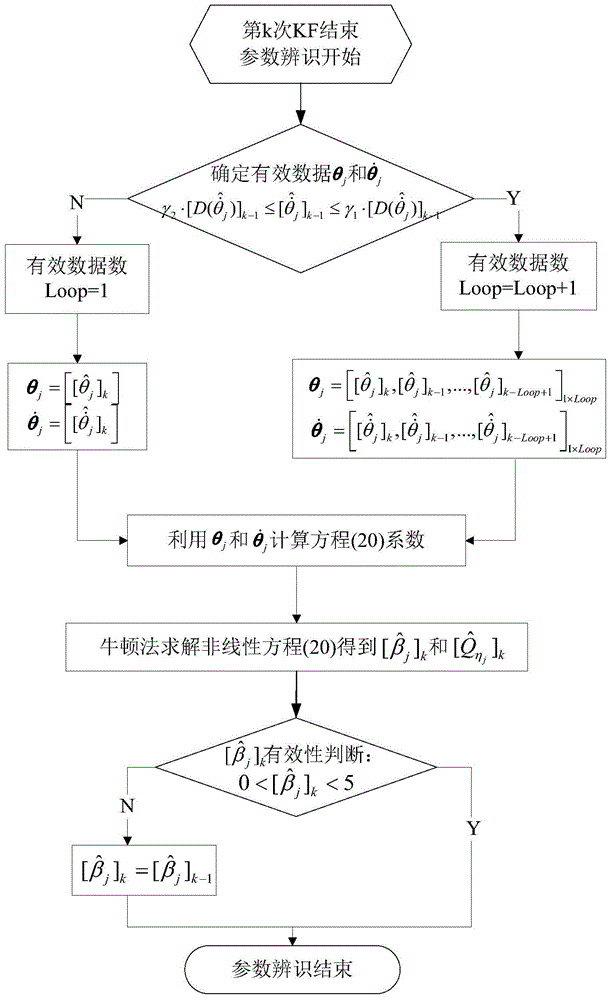
本发明的技术解决问题是：克服现有技术的不足，提出一种基于参数辨识的机载分布式POS传递对准方法，该方法可提高载机机体存在弹性变形时分布式POS的传递对准精度。本发明的技术解决方案为：一种基于参数辨识的机载分布式POS传递对准方法。其具体步骤如下：(1)将机体弹性变形角视为二阶马尔科夫过程，建立包含子IMU惯导误差模型和角误差模型的传递对准误差模型；(2)将机体弹性变形角和弹性变形角速度扩充为状态变量，并将高精度主POS与子IMU的速度和姿态之差作为量测，建立子IMU传递对准的数学模型；(3)采用卡尔曼滤波估计出tk时刻的弹性变形角和弹性变形角速度k＝0,1,2,...,N-1，利用估计出的和在线计算并更新描述弹性变形角的二阶马尔科夫过程的参数；(4)将更新后的二阶马尔科夫过程参数作为下一时刻tk+1的滤波初始值，采用卡尔曼滤波估计出更加准确的tk+1时刻的子IMU姿态误差、速度误差和位置误差，利用上述误差修正子IMU的捷联解算结果，得到tk+1时刻子IMU的位置、速度和姿态。上述步骤(1)中传递对准误差模型包括子IMU惯导误差模型和主子系统间的角误差模型。具体传递对准误差建模步骤为：1)建立子IMU惯导误差模型相关参考坐标系的定义包括：记i为地心惯性坐标系；e为地球坐标系；主POS和子IMU导航坐标系均为东北天地理坐标系，分别用n和n1表示；载体坐标系原点为载体重心，x轴沿载体横轴向右，y轴沿载体纵轴向前，z轴沿载体竖轴向上，该坐标系固定在载体上，称为右前上载体坐标系，用a和b分别代表主POS和子IMU的载体坐标系；根据上述定义，子IMU惯导误差模型为：a)姿态角误差微分方程：b)速度误差微分方程：c)位置误差微分方程：d)惯性仪表误差微分方程：其中为子IMU姿态失准角，φE、φN和φU分别为东向、北向、天向失准角，下标E、N和U分别表示东向、北向和天向；为子IMU导航系相对惯性系的角速度；为的误差角速度；为子IMU载体系到其导航系的姿态阵的估计值；和分别为子IMU速度和速度误差，其中VE、VN和VU分别为东向、北向和天向速度，δVE、δVN和δVU分别为东向、北向和天向速度误差；是子IMU的比力，其中fE、fN和fU分别为东向、北向和天向比力；和分别为子IMU导航系相对地球坐标系的角速度及其误差；和分别为子IMU导航系相对地球坐标系的角速度及其误差；L、λ、H和δL、δλ、δH分别为子IMU纬度、经度、高度和纬度误差、经度误差、高度误差；为纬度的一阶导数，为经度的一阶导数；RM和RN分别为沿子午圈和卯酉圈的主曲率半径；εb＝[εxεyεz]T和分别为子IMU陀螺常值漂移和加计常值偏置，其中εx、εy和εz分别为子IMU载体系x轴、y轴和z轴陀螺常值漂移，其中和分别为子IMU载体系x轴、y轴和z轴加计常值偏置。2)建立主子系统间的角误差模型a)固定安装误差角ρ的微分方程：其中ρ＝[ρxρyρz]T为子IMU固定安装误差角，ρx、ρy和ρz分别为子IMU载体系x轴、y轴和z轴安装误差角。b)弹性变形角的微分方程：其中θj为子IMU载体系第j轴上的弹性变形角，j＝x,y,z，θ＝[θxθyθz]T为弹性变形角；βj＝2.146/τj，τj为二阶马尔科夫过程相关时间；ηj为零均值白噪声，其方差满足：σj2为弹性变形角θj的方差，βj和为描述弹性变形角θ的二阶马尔科夫过程的参数。上述步骤(2)建立的子IMU传递对准数学模型为：Z＝HX+V其中系统状态变量X为：X＝[X1X2]T系统转移矩阵F可由子IMU的传递对准误差模型确定；系统噪声其中和分别为子IMU载体系x轴、y轴、z轴陀螺和子IMU载体系x轴、y轴、z轴加速度计的随机误差，不包括随机常值误差；系统噪声W为零均值的高斯白噪声，其方差阵Q由陀螺常值漂移、加计常值偏置和二阶马尔科夫过程参数Qηj决定；系统噪声阵G的表达式为：其中为子IMU载体系到导航系的姿态转换矩阵。系统量测变量Z＝[δψδθδγδV′EδV′NδV′U]T，其中δψ、δθ、δγ和δV′E、δV′N、δV′U分别为子IMU与主POS的航向角、俯仰角、横滚角之差和东向、北向、天向速度之差；量测噪声其中vδψ、vδθ、vδγ分别为主POS航向角、俯仰角、横滚角的量测噪声，分别为主POS东向、北向、天向速度的量测噪声；V为零均值的高斯白噪声，其方差阵R由主POS的位置和速度精度决定；量测矩阵H为：令主POS姿态矩阵记为矩阵Ta中第l行、第m列的元素，l＝1,2,3，m＝1,2,3；则上式中和的表达式为：上述步骤(3)所采用的利用子IMU安装点处tk时刻的弹性变形角估计值和弹性变形角速度估计值在线辨识描述弹性变形角的二阶马尔科夫过程参数βj和的具体步骤为：1)确定有效数据θj和记和的有效数据数为Loop，初始t0时刻Loop＝1；当tk时刻弹性变形角速度估计值满足时，Loop＝Loop+1，反之，Loop＝1，其中[·]k中下标k表示tk时刻，D(·)表示方差，γ1＝2和γ2＝0.1分别为上界阈值参数和下界阈值参数；2)计算tk时刻参数和初始t0时刻，βj和初始值为和a)利用向量θj和计算方差和协方差b)给定迭代初值为用牛顿法求解如下所示的以βj为自变量的非线性方程，即可得到二阶马尔科夫过程参数和其中记3)参数估计结果的有效性判断当tk时刻参数βj的估计值不满足时，令上述步骤(4)中将更新后的二阶马尔科夫过程参数作为下一时刻tk+1的滤波初始值，采用卡尔曼滤波估计出子IMU姿态误差、速度误差和位置误差，最终修正子IMU捷联解算结果的步骤为：1)估计子IMU的姿态误差、速度误差和位置误差将tk时刻计算出的二阶马尔科夫过程参数和作为下一时刻tk+1的滤波初始值，采用卡尔曼滤波估计出tk+1时刻的子IMU平台失准角φE、φN、φU、速度误差δVE、δVN、δVU和位置误差δL、δλ、δH；2)利用上述误差修正子IMU的捷联解算结果，得到tk+1时刻的子IMU位置、速度和姿态a)速度修正其中和分别为子IMU修正后的东向、北向和天向速度；和分别为子IMU捷联解算得到的东向、北向和天向速度；δVE、δVN和δVU分别为tk+1时刻卡尔曼滤波估计出的子IMU捷联解算东向、北向和天向速度误差；b)位置修正Lnew＝Lold-δLλnew＝λold-δλHnew＝Hold-δH其中Lold、λold和Hold分别为子IMU捷联解算得到的纬度、经度和高度；Lnew、λnew和Hnew分别为子IMU修正后的纬度、经度和高度；δL、δλ和δH分别为tk+1时刻卡尔曼滤波估计出的子IMU捷联解算纬度、经度和高度误差；c)姿态修正计算tk+1时刻子IMU地理坐标系n1与计算地理坐标系n′1间的转换矩阵计算tk+1时刻子IMU载体坐标系b与真实地理坐标系n1之间的转换矩阵其中为tk+1时刻子IMU捷联解算得到的姿态矩阵；由被更新后的子IMU的姿态阵计算tk+1时刻子IMU的航向角ψs、俯仰角θs和横滚角γs，将记为其中Tlm为矩阵中第l行、第m列的元素，l＝1,2,3，m＝1,2,3；则子IMU航向角ψs、俯仰角θs和横滚角γs的主值，即ψs主、θs主和γs主分别为：θs主＝arcsin(T32)由于航向角ψs、俯仰角θs和横滚角γs的取值范围分别定义为[0，2π]、[-π，+π]；那么，ψs、θs和γs的真值可由下式确定：θs＝θs主通过对子IMU的速度、位置和姿态进行修正，能够得到更加准确的子IMU安装点的速度、位置和姿态信息，完成传递对准。本发明与现有技术相比的优点在于：针对实际应用中描述机体弹性变形的马尔科夫过程参数未知且时变的问题，利用传递对准中高精度主POS的速度和姿态信息能够对子IMU状态变量进行修正的有利条件，利用卡尔曼滤波估计出的弹性变形角和弹性变形角速度来计算马尔科夫过程参数，从而实现了该参数的在线辨识。克服了传统的、凭经验确定的固定参数方法无法真实描述机体弹性变形导致传递对准精度低的不足，且不受载机材质的约束以及是否外挂载荷的影响，提高了系统状态模型和噪声统计特性的准确性，从而提高了传递对准的精度。附图说明图1为本发明的流程图；图2为本发明的二阶马尔科夫过程参数辨识方法的流程图；具体实施方式如图1所示，本发明的具体方法实施如下：1、建立包含子IMU惯导误差模型和主子系统间角误差模型的传递对准误差模型具体的传递对准误差建模步骤为：(1)建立子IMU惯导误差模型相关参考坐标系的定义包括：记i为地心惯性坐标系；e为地球坐标系；主POS和子IMU导航坐标系均为东北天地理坐标系，分别用n和n1表示；载体坐标系原点为载体重心，x轴沿载体横轴向右，y轴沿载体纵轴向前，z轴沿载体竖轴向上，该坐标系固定在载体上，称为右前上载体坐标系，用a和b分别代表主POS和子IMU的载体坐标系；根据上述定义，子IMU惯导误差模型为：a)姿态角误差方程：b)速度误差方程：c)位置误差方程：d)惯性仪表误差方程：其中为子IMU姿态失准角，φE、φN和φU分别为东向、北向、天向失准角，下标E、N和U分别表示东向、北向和天向；为子IMU导航系相对惯性系的角速度；为的误差角速度；为子IMU载体系到其导航系的姿态阵的估计值；和分别为子IMU速度和速度误差，其中VE、VN和VU分别为东向、北向和天向速度，δVE、δVN和δVU分别为东向、北向和天向速度误差；是子IMU的比力，其中fE、fN和fU分别为东向、北向和天向比力；和分别为子IMU导航系相对地球坐标系的角速度及其误差；和分别为子IMU导航系相对地球坐标系的角速度及其误差；L、λ、H和δL、δλ、δH分别为子IMU纬度、经度、高度和纬度误差、经度误差、高度误差；为纬度的一阶导数，为经度的一阶导数；RM和RN分别为沿子午圈和卯酉圈的主曲率半径；εb＝[εxεyεz]T和分别为子IMU陀螺常值漂移和加计常值偏置，其中εx、εy和εz分别为子IMU载体系x轴、y轴和z轴陀螺常值漂移，其中和分别为子IMU载体系x轴、y轴和z轴加计常值偏置。(2)建立主子系统间的角误差模型主子系统间的角误差模型由子IMU固定安装误差角ρ＝[ρxρyρz]T和机体弹性变形角θ＝[θxθyθz]T共同决定，其中ρx、ρy和ρz分别为子IMU载体系x轴、y轴和z轴安装误差角，θx、θy和θz分别为子IMU载体系x轴、y轴和z轴弹性变形角。a)固定安装误差角ρ的微分方程：b)弹性变形角的微分方程：其中j＝x,y,z，βj＝2.146/τj，τj为二阶马尔科夫过程相关时间；ηj为零均值白噪声，其方差满足：σj2为弹性变形角θj的方差。βj和为描述弹性变形角θ的二阶马尔科夫过程的参数。2、建立子IMU传递对准的数学模型根据1中机载分布式POS传递对准误差模型将机体弹性变形角和弹性变形角速度扩充为状态变量，并将高精度主POS与子IMU的速度和姿态之差作为量测，建立子IMU传递对准的数学模型为：其中系统状态变量X为：X＝[X1X2]T系统转移矩阵F可由子IMU的传递对准误差模型确定；系统噪声其中和分别为子IMU载体系x轴、y轴、z轴陀螺和子IMU载体系x轴、y轴、z轴加速度计的随机误差，不包括随机常值误差；系统噪声W为零均值的高斯白噪声，其方差阵Q由陀螺常值漂移、加计常值偏置和二阶马尔科夫过程参数决定；系统噪声阵G的表达式为：其中为子IMU载体系到导航系的姿态转换矩阵。系统量测变量Z＝[δψδθδγδV′EδV′NδV′U]T，其中δψ、δθ、δγ和δV′E、δV′N、δV′U分别为子IMU与主POS的航向角、俯仰角、横滚角之差和东向、北向、天向速度之差；量测噪声其中vδψ、vδθ、vδγ分别为主POS航向角、俯仰角、横滚角的量测噪声，分别为主POS东向、北向、天向速度的量测噪声；V为零均值的高斯白噪声，其方差阵R由主POS的位置和速度精度决定；量测矩阵H为：令主POS姿态矩阵记为矩阵Ta中第l行、第m列的元素，l＝1,2,3，m＝1,2,3；则上式中和的表达式为：3、在线辨识描述弹性变形角的二阶马尔科夫过程参数采用卡尔曼滤波估计出子IMU安装点处tk时刻(k＝0,1,2,...,N-1)的弹性变形角和弹性变形角速度估计值和利用估计出的和在线辨识描述弹性变形角的二阶马尔科夫过程参数βj和的具体步骤为：(1)采用卡尔曼滤波估计出子IMU安装点处tk时刻的弹性变形角和弹性变形角速度估计值初始t0时刻给定卡尔曼滤波算法编排如下：状态一步预测方程其中Φk,k-1分别为tk时刻系统状态一步预测值、tk-1时刻系统状态估值、tk-1时刻到tk时刻的系统状态转移矩阵；状态估值计算方程其中Kk、Zk、Hk分别为tk时刻系统状态估值、系统增益矩阵、量测向量和量测矩阵；滤波增益方程其中Pk/k-1、Rk分别为tk时刻系统协方差阵的一步预测、tk时刻系统量测噪声矩阵；一步预测均方误差方程其中，Pk-1、Qk-1、Γk-1分别为tk-1时刻系统协方差阵、tk-1时刻系统噪声矩阵、tk-1时刻系统噪声驱动矩阵；估计均方误差方程其中，Pk为tk时刻系统状态协方差阵，I为单位阵。(2)二阶马尔科夫过程参数辨识利用卡尔曼滤波估计出子IMU安装点处tk时刻的弹性变形角和弹性变形角速度估计值和可以在线辨识并更新描述弹性变形角的二阶马尔科夫过程参数βj和具体的参数辨计算步骤为：a)确定有效数据θj和在滤波过程中二阶马尔科夫过程参数可能会在某时刻发生较大变化，此时再利用参数变化前的估计值和计算非线性方程系数会导致过程参数估计值存在较大误差，因此必须在参数辨识方法中加入确定和有效数据θj和的部分。针对根据弹性变形角速度能够有效反映系统状态模型参数βj变化的特点设计参数辨识方法中对于参数变化的判断部分，从而确定有效数据θj和判断条件的设置原理可以简述为给定估计值一个置信区间，即当与参数相关的估计值属于置信区间时，即认为该时刻相关参数并未发生改变，反之则判定参数发生改变。具体判断条件为：其中[·]k中下标k表示时刻tk，D(·)表示方差，γ1＝2和γ2＝0.1分别为上界和阈值参数下界阈值参数。记和的有效数据数为Loop，初始t0时刻Loop＝1。确定有效数据θj和的具体步骤为：当tk时刻弹性变形角速度估计值满足时，Loop＝Loop+1，反之，Loop＝1，b)计算tk时刻参数和由于弹性变形角θj符合式(6)所示的二阶马尔科夫过程，对(6)左右两边取方差，结合式(7)可以得到：其中用牛顿法求解以βj为自变量的非线性方程(20)即可得到二阶马尔科夫过程参数和在实际情况下，飞机弹性变形相关时间τj>0并且大于或等于1。因此，tk时刻牛顿法迭代之前给定迭代初值初始t0时刻，βj和初始值为和计算tk时刻参数和的具体步骤为：i)利用向量θj和计算方差和协方差ii)给定迭代初值为用牛顿法求解如下所示的以βj为自变量的非线性方程(20)，即可得到二阶马尔科夫过程参数和记c)参数估计结果的有效性判断由于非线性方程牛顿法求得的解为最靠近初值的近似解，因此需要判断迭代近似解的有效性。由于在实际情况下，飞机弹性变形相关时间τj>0并且大于或等于1，因此对于迭代解有效性的判断可以给出如下判断条件：其中为tk时刻通过方程(20)计算出的该时刻参数βj的估计值。参数有效性判断部分可以简述为：当tk时刻参数βj的估计值不满足时，令二阶马尔科夫参数辨识方法的具体流程图如图2所示。4、修正子IMU捷联解算得到的速度、位置、姿态信息将更新后的二阶马尔科夫过程参数作为下一时刻tk+1的滤波初始值，从而估计出更加准确的子IMU姿态误差、速度误差和位置误差，利用该估计误差修正子IMU的捷联解算结果，计算出更加准确的子IMU位置、速度和姿态。具体的修正步骤为：(1)估计子IMU的姿态误差、速度误差和位置误差将tk时刻计算出的二阶马尔科夫过程参数和作为下一时刻(tk+1)的滤波初始值，采用卡尔曼滤波估计出tk+1时刻的子IMU平台失准角(φE、φN、φU)、速度误差(δVE、δVN、δVU)和位置误差(δL、δλ、δH)。a)速度修正其中和分别为子IMU修正后的东向、北向和天向速度；和分别为子IMU捷联解算得到的东向、北向和天向速度；δVE、δVN和δVU分别为tk+1时刻卡尔曼滤波估计出的子IMU捷联解算东向、北向和天向速度误差。b)位置修正其中Lold、λold和Hold分别为子IMU捷联解算得到的纬度、经度和高度；Lnew、λnew和Hnew分别为子IMU修正后的纬度、经度和高度；δL、δλ和δH分别为tk+1时刻卡尔曼滤波估计出的子IMU捷联解算纬度、经度和高度误差。c)姿态修正计算tk+1时刻子IMU地理坐标系n1与计算地理坐标系n′1间的转换矩阵计算tk+1时刻子IMU载体坐标系b与真实地理坐标系n1之间的转换矩阵其中为tk+1时刻子IMU捷联解算得到的姿态矩阵。由被更新后的子IMU的姿态阵计算子IMU安装点的航向角ψs，俯仰角θs和横滚角γs。将记为又因为其中Tlm为矩阵中第l行、第m列的元素，l＝1,2,3，m＝1,2,3；则子IMU航向角ψs、俯仰角θs和横滚角γs的主值，即ψs主、θs主和γs主分别为：由于航向角ψs、俯仰角θs和横滚角γs的取值范围分别定义为[0，2π]、[-π，+π]。那么，ψs、θs和γs的真值可由下式确定：θs＝θs主(30)通过对子IMU的速度、位置和姿态进行修正，能够得到更加准确的子IMU安装点的速度、位置和姿态信息，完成传递对准。本发明说明书中未作详细描述的内容属于本领域专业技术人员公知的现有技术。