一种伽玛探测器无源效率刻度新方法与流程

本发明涉及一种无源效率刻度方法，尤其涉及一种伽玛探测器无源效率刻度新方法。

背景技术：

伽玛谱仪是放射性核素定性分析和定量测量中最广泛使用的仪器之一，伽玛能谱分析方法具有速度快、精度高以及可以做到非破坏性测量等优点，因此被广泛应用到了科学研究等的各个相关领域中。

为了测量待测放射源中放射性物质的含量，首先需要对伽玛谱仪进行效率刻度。所谓效率刻度是指，建立待测放射源中单位时间内放射出的能量为E的伽玛粒子数与伽玛谱仪中相应能量的全能峰计数率之间的比例关系。伽玛谱仪的效率刻度主要有两种方法，一是相对测量方法，二是无源效率刻度方法。

相对测量方法首先需要制备一系列已知放射性核素种类和活度的标准源或者标准样品。对标准源进行测量，获得能量为E的伽玛粒子的效率刻度因子ε(E)＝n_标(E)/A_标(E)，其中A_标(E)为标准源单位时间内放出的能量为E的伽玛粒子数，n_标(E)为探测器相应全能峰的计数率。当待测对象的几何形状、核素分布、样品载体成分等与标准源或者标准样品完全一致时，利用公式A_样(E)＝n_样(E)/ε(E)即可得到待测样品中单位时间内放射出的能量为E的伽玛粒子数。

相对测量方法具有如下局限：1、需要制备标准放射源或者标准样品源，对于短寿命核素，还需要不断更新标准源。2、需要已知标准源或样品源以及待测对象的成分、几何形状、核素分布，当待测对象与标准源不同时，需要进行自吸收校正和几何校正，这是很麻烦的工作。3、对于野外测量或者非破坏性测量(体源)测量，难以制备合适的标准源。4、增加标准放射源的管理工作。5、 速度慢。

无源效率刻度方法利用数值计算获得任意体源的效率刻度曲线。该方法具有不需要制备标准源、可以对任意体源进行效率刻度、速度快等优点，部分地克服了相对测量方法的缺点，拓展了伽玛谱仪的适用范围，提高了伽玛谱仪的定量分析能力。因此，建立无源效率刻度方法并编制相应的软件受到了国际间的重视。

1981年，Moens等给出了体源效率刻度的一般的数学描述形式，该方法需要详细的探测器结构信息和非常长的计算时间。为了减小计算耗费时间，Noguchi等在文献中建议把体源和探测器等效为两个点以及射线路径上的屏蔽材料，但是，在建立探测器晶体的效率中心的过程中却需要大量的空间中点源的实验测量结果，同时为了得到好的刻度精度，需要确定大量的经验参数。Atrashkevich and Kolotov在文献中提出了一种新的方法以进一步减少文献中方法所需要的点源效率测量数据，该方法一方面仍然需要许多实验测量，另外只能刻度探测器端面外法线方向半径为10厘米范围内的体源。另外Kamboj和Kahn以及F.Bronson和L.Wang对无源效率刻度方法进行过系统的研究，两者都采用Monte Carlo方法作为主要的计算方法，采用实验测量的结果确定其中的校正因子。但是前者提出的方法只适用于轴(探测器对称轴)对称几何的体源，后者的方法在建模和计算方面都需要大量的时间。

技术实现要素：

本发明的目的就在于为了解决上述问题而提供一种伽玛探测器无源效率刻度新方法。

本发明通过以下技术方案来实现上述目的：

本发明包括以下步骤：

a、以给定的探测器结构参数范围，包括晶体死层等几何尺寸，作为初始值的取值范围，利用蒙特卡罗(Monte_Carlo)计算并与实验测量结果比较得到该探测器的真实结构参数；

b、根据真实结构参数利用蒙特卡罗或离散纵坐标方法计算探测器表面上的点源从任意角度发射出的特定能量的射线在探测器中的全能峰探测效率，以此表征该探测器；

c、利用该探测器表征结果，通过数值积分方法计算任意伽玛放射源，包括体源、面源和点源的多个能量点的全能峰探测效率，根据多个能量点的探测效率拟合探测效率刻度曲线。

进一步，根据步骤a，包括以下步骤：

A、选择一系列不同能量和已知活度的放射源，在不同位置测量其探测效率；

B、然后在探测器的可能的参数范围内取不同的探测器结构参数组，用蒙特卡罗方法或者其他数值方法计算这些点源的探测效率；

C、把计算结果与实验结果比较，两者相差满足误差要求者，计算所采用的参数组即为探测器的真实参数。

本发明的有益效果在于：

本发明提供一种伽玛探测器无源效率刻度新方法，该方法具有测量工作量小、计算精度高、体源的位置不受限制等优点。

附图说明

图1为第一类探测器示意图；

图2为光子从探测器端面入射时第一类γ探测器表征方法示意图；

图3为光子从探测器侧面入射时第一类γ探测器表征方法示意图；。

图4为光子从探测器侧面入射时第二类γ探测器表征方法示意图；

图5为第一类γ探测器无源效率刻度原理示意图。

具体实施方式

下面结合附图对本发明作进一步说明：

如图1所示：本发明包括以下步骤：

d、以给定的探测器结构参数范围(包括晶体死层等几何尺寸)作为初始值的取值范围，利用蒙特卡罗(Monte_Carlo)计算并与实验测量结果比较得到该探测器的真实结构参数；

e、根据真实结构参数利用Monte_Carlo或离散纵坐标(SN)方法计算探测器表面上的点源从任意角度发射出的特定能量的射线在探测器中的全能峰探测效率，以此表征该探测器；

f、利用该探测器表征结果，通过数值积分方法计算任意伽玛放射源，包括体源、面源和点源的多个能量点的全能峰探测效率，根据多个能量点的探测效率拟合探测效率刻度曲线。

根据步骤a，包括以下步骤：

A、选择一系列不同能量和已知活度的放射源，在不同位置测量其探测效率；然后在探测器的可能的参数范围内取不同的探测器结构参数组，用蒙特卡罗方法或者其他数值方法计算这些点源的探测效率；

B、把计算结果与实验结果比较，两者相差满足误差要求者，计算所采用的参数组即为探测器的真实参数。

实施例一：

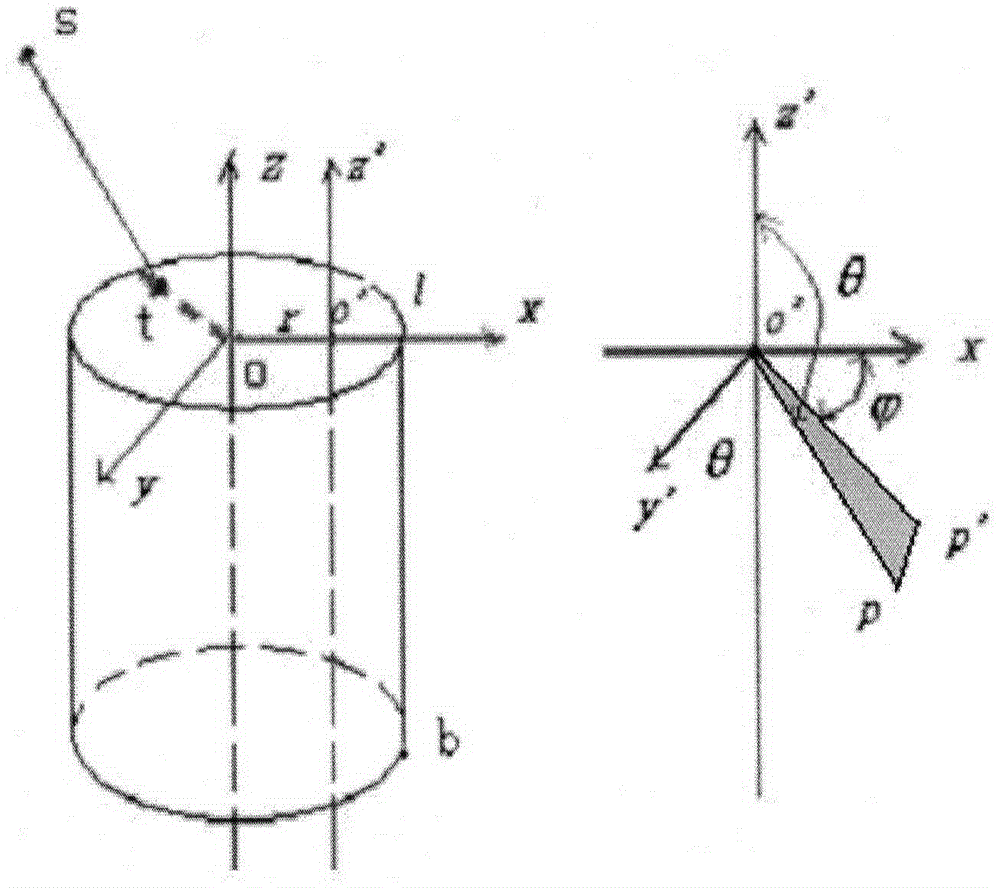
如图1、图2和图3所示，第一类探测器为圆柱体的探测器，其方法为：

ot为探测器对称轴，R为探测器端面中心到边缘的垂直距离。H为探测器上下端面之间的垂直距离。对于这种类型的探测器，分两步表征探测器：

(1)在ol上取一系列点，计算这些点发射出的能量为E的任意方向的射线的探测效率。即计算其探测效率的角分布E为粒子能量，r、θ和如图2所示，定义如下：以探测器端面圆心为坐标原点，端面任意一径向外方向为x轴正向，端面外法线方向为z轴正向，建立坐标系o(x，y，z)，以o(x，y，z)坐标系为基准坐标系，r为ol上任意一点o′到到轴心o的距离，o′p为o′上的点源向探测器方向(z＜0)发射的任意一条射线，以o′为坐标原点，o′到l方向为x′轴正向，探测器端面外法线方向为z′轴正向，建立坐标系o′(x′，y′，z′)，可以看出，o′(x′，y′，z′)坐标系为o(x，y，z)坐标系沿x轴正向平移r距离后获得。o′p′为o′p在x′xy′平面的投影，θ为o′p与z′轴的夹角，为o′p′与x轴正向的夹角。

(2)在lb上取坐标为h点，计算这些点发射出的能量为E的方向为θ和的射线的探测效率，即计算其探测效率的角分布E为粒子能量，h、θ和 如图3所示，定义如下：

h为lb上任意一点o″到l的距离，o″p为o″上的点源向探测器方向(x＜0)发射的任意一条射线，以o″为坐标原点，x′轴平行于x轴，x′轴正向与x轴正向相同，z′轴平行于z轴，z′轴正向与z轴正向相同，由此建立坐标系o″(x′，y′，z′)，可以看出，o′(x′，y′，z′)坐标系为基准坐标系o(x，y，z)沿x轴正向平移R，沿z轴负向平移h距离后获得。o″p″为o″p在x′×y′平面的投影，θ为o″p与z′轴的夹角，为o″p″与x′轴的夹角。

(3)和即为探测器的表征函数。

实施例二：

如图4所示，第二类探测器为井型的探测器，其结构及光子从探测器侧面入射时的表征方法。

oo”’为探测器对称轴，r1为探测器端面中心到探测器内边缘的垂直距离，r2为探测器端面中心到探测器外边缘的垂直距离。H为探测器上下端面之间的垂直距离。对于这种类型的探测器，分两步表征探测器：

(1)在o”’b上取一系列点，计算这些点发射出的能量为E的伽玛射线的任意方向的射线的探测效率。即计算其探测效率的角分布其中，o”’为探测器井底端面对称中心，b为探测器内壁与井底端面的交线上任意一点。E、r、θ和的定义与第一类探测器表征方法的步骤(1)中的定义相同。

(2)在o′b上取一系列点，计算在这些点上的点源发射的能量为E的γ射线的探测效率的角分布其中r、θ和定义为：

以探测器前端面对称中心为坐标原点，端面外法线方向为z轴正方向，端面上探测器任一径向为x轴，由此确定一直角坐标系o(x，y，z)。o′b为探测器内壁侧面上任一条线段，o′为o′b与探测器上端面的交点，o′b垂直于探测器上下端面。令o″为o′b上任意一点，o″与o′的距离为h，o″的坐标为((-r₁，0，-h)。o″为坐标原点建立新坐标系o(x′，y′，z′)，x′、y′和z′轴分别平行于x、y和z轴。其中θ为点源o″在x′≤0的半无穷空间内发射的能量为E的γ射线o″p与z′轴的夹角，为点源o″在x′≤0的半无穷空间内发射的能量为E的γ射线o″p在y′xx′平面内的投影o″p″与x′轴的夹角。

(3)和即为第二类探测器的表征函数。

本发明的工作原理如下：

如图5所示，第一类伽玛探测器刻度方法的基本原理为：

V为任意体源，dv为源V中的小体源，S₁为探测器端面相对于dv所张区域，S₂为探测器侧面相对于dv所张区域。假设源dv的能量为E的粒子的发射率为τ×dv，τ为V中单位体积内向4π方向发射的能量为E的粒子的发射率。

令cos(ω)×φ为探测器端面对dv所张立体角，sin(ω)dω×dφ为cos(ω)×φ的微元。则单位时间内源dv在立体角sin(ω)dω×dφ内发射的能量为E的粒子数为

$n\left(E\right)=\frac{\mathrm{\τ}}{4\mathrm{\π}}\×\sin \left(\mathrm{\ω}\right)\mathrm{d\ω}\×\mathrm{d\φ}\×\mathrm{dv}$

设在sin(ω)dω×dφ立体角内从dv发射出的粒子，未经过能量损失到达探测器上表面，在探测器内的全能峰探测效率为f_eff(E，ω，φ)；设在sin(ω)dω×dφ立体角内从dv发射出的粒子穿透屏蔽层(包括源的自吸收层)，且没有发生能量损失的穿透率为f_att(E，ω，φ)。则源V发射出的能量为E的粒子在探测器端面的探测效率为：

${\mathrm{\ϵ}}_{\mathrm{eff},S_1}\left(E\right)=\underset{V,\mathrm{\ω}\×\mathrm{\φ}}{\∫}\frac{1}{4\mathrm{\πV}}{f}_{\mathrm{att}}(e,\mathrm{\ω},\mathrm{\φ})f_{\mathrm{eff}}(e,\mathrm{\ω},\mathrm{\φ})\×\sin \left(\mathrm{\ω}\right)\mathrm{d\ω}\×\mathrm{d\φ}\×\mathrm{dv}---\left(1\right)$

设cos(ω′)×φ′为探测器侧面对dv所张立体角，sin(ω′)dω′×dφ′为cos(ω′)×φ′的微元。则源V发射出的能量为E的粒子在探测器侧面的探测效率为：

${\mathrm{\ϵ}}_{\mathrm{eff},S_2}\left(E\right)=\underset{V,{\mathrm{\ω}}^{\′}\×{\mathrm{\φ}}^{\′}}{\∫}\frac{1}{4\mathrm{\πV}}{f}_{\mathrm{att}}(e,{\mathrm{\ω}}^{\′},{\mathrm{\φ}}^{\′})f_{\mathrm{eff}}(e,{\mathrm{\ω}}^{\′},{\mathrm{\φ}}^{\′})\×\sin \left({\mathrm{\ω}}^{\′}\right)d{\mathrm{\ω}}^{\′}\×d{\mathrm{\φ}}^{\′}\×\mathrm{dv}---\left(2\right)$

探测器对源V的能量为E的粒子的探测效率为

${\mathrm{\ϵ}}_{\mathrm{eff}}\left(E\right)={\mathrm{\ϵ}}_{\mathrm{eff},S_1}\left(E\right)+{\mathrm{\ϵ}}_{\mathrm{eff},S_2}\left(E\right)---\left(3\right)$

对于第二类探测器，公式(1)、(2)和(3)同样成立，只不过公式(1)针对源粒子打到探测器内壁侧面的情况，公式(2)针对源粒子打到探测器内壁底部的情况。

计算ε_eff(E)的基本步骤为：

(1)把体源离散成为m个小体源的组合。

(2)把小体源中心点发射出的能量为E的射线按照角度离散成mm条射线。

(3)计算第i个小体源中心发射出的第ii条射线打到探测器的位置，第ii条射线的出射方位角为(ω，φ)。如果射线打到探测器端面，计算出 相应的并获得该条射线的探测效率即对应于公式(1)中的f_eff(E，ω′，φ′)。如果射线打到探测器侧面，则计算并得到该条射线的探测效率即对应于公式(2)中的f_eff(E，ω′，φ′)。如果没有打到探测器上，则该射线的探测效率为0。

(4)按照如下公式计算该条射线的衰减因子：

$f_{\mathrm{att}}(E,\mathrm{\ω},\mathrm{\φ})=\exp (-\underset{j=1}{\overset{J}{\mathrm{\Σ}}}\left({\mathrm{\Φ}}_j{l}_j\right))$

其中J为射线路径上经过的材料总数量，Φ_j为第j种

材料的宏观截面，l_j为射线穿过第j种材料的距离。

(5)重复(3)，直到mm条射线的探测效率都计算完毕。

(6)对所有mm条射线的探测效率求和，并除以mm得到第i个点源的探测效率。

(7)把第i个点源按照粒子出射角度进一步细分，重复(3)到(6)步。直到相邻两次的讨算结果之差约等于零。

(8)对所有的小体源重复(2)到(6)。得到所有小体源的探测效率，求和这些小体源的探测效率并除以m，得到体源的探测效率。

(9)把体源进一步细分成更小的小体源，重复(2)到(8)，如果两次的结果之差约等于零，则输出体源的能量为E的伽玛射线的全能量峰的探测效率。

(10)取多个不同的能量，重复(2)到(9)得到多个不同能量的伽玛射线的全能量峰的探测效率。

(11)利用不同能量的全能峰探测效率计算结果，按照如下公式拟合效率刻度曲线。

$\ln \left(\mathrm{\ϵ}\right)=a_0+\underset{i}{\overset{N}{\mathrm{\Σ}}}{a}_i{\ln }^i\left(E\right)---\left(4\right)$

其中拟合的阶次一般取为5或者6。具体地，可以采用最小二乘方法拟合出公式(4)中的系数。

本领域技术人员不脱离本发明的实质和精神，可以有多种变形方案实现本发明，以上所述仅为本发明较佳可行的实施例而已，并非因此局限本发明的权利范围，凡运用本发明说明书及附图内容所作的等效结构变化，均包含于本发明的权利范围之内。