基于时空域优化的交错网格正演模拟方法与流程

本发明属于地球物理处理技术，是一种基于时空域优化的交错网格正演模拟方法。

背景技术：

随着地震勘探开发的深入，对地震波场正演模拟精度、地下成像结果分辨率等要求越来越高，基于波场延拓的逆时偏移成像、最小二乘逆时偏移以及全波形反演成像已经成为研究的热点，波场延拓的效率与精度直接影响后续成像和反演的效率和精度。有限差分法兼顾计算效率与模拟精度，目前已经广泛应用于勘探地震的波场延拓中。有限差分法利用离散的差分算子逼近连续的偏导算子，在计算中通常存在数值频散，影响地震波波场模拟精度。

常规的有限差分系数基于零波数处的泰勒展开求取，在低波数段能较精确地模拟地震波传播，但在高波数段会出现严重的数值频散。如何改进差分算子以压制数值频散是有限差分正演模拟研究的重要领域。目前针对数值频散国内外许多研究人员开展了大量研究工作，常用的策略主要包括：(1)减小空间和时间采样间隔；(2)增加时间或者空间差分阶数；(3)通量传输校正法(FCT)。如公开号为专利技术CN103823239A的专利公开了一种频率域优化混合交错网格有限差分正演模拟方法，该方法的步骤为：①给出时间域二维声波方程；②消除人工边界反射，得带完全匹配层边界条件的时间域二维声波方程；③对方程左右两边时间变量进行傅立叶变换得频率域声波方程；④对匹配层边界条件频率域声波方程按常规交错网格进行有限差分离散，得有限差分离散格式；⑤对匹配层边界条件频率域声波方程按旋转交错网格进行有限差分离散得有限差分离散格式；⑥将常规交错网格和旋转交错网格优化混合，用两套网格系统中的加权平均，质量加速项为中心点与其周围8点的加权平均；⑦在相速度误差最小的准则下，求取最优化系数。该发明加权系数使有限差分离散引起的频散误差减小，提高了频率域正演模拟的精度。这三种方法虽在一定程度上改善了数值频散，但都导致了计算量的增加。目前，计算量大仍然是制约三维高精度勘探、基于反演思想的最小二乘偏移、全波形反演、各向异性相关研究等推广应用的重要因素。无论是减少时空采样间隔，提高差分阶数，还是FCT校正，在理论方法实用化中优势和不足都较为明显。

另外，目前有关有限差分正演优化的研究大都建立在二阶声波方程的基础上，对一阶变密度声波方程研究较少。然而，真实地下介质既存在速度变化也存在密度的变化， 大量事实表明一阶压强-速度方程更加利于处理变密度介质。

技术实现要素：

本发明目的在于提供一种可有效压制数值频散，并在一定程度上提高地震波群速度计算精度的交错网格正演模拟方法，该方法以一阶声波方程组的数值模拟为研究对象，推导出一阶声波方程中的压强场与偏振速度场的解析表达式，据此给出了一种高精度的递推格式，使用最小二乘法在有效波数段求取匹配系数，考虑到系数求解的病态性，采用预处理的共轭梯度迭代算法，在处理变密度介质时，既能较好压制数值频散，同时可以提高群速度精度。本发明的具体方法如下。

一种基于时空域优化的交错网格正演模拟方法，包括如下步骤：

步骤1：给出一阶压强-速度偏微分方程组形式，求出其平面波通解，得到一阶声波方程中的压强场与偏振速度场的解析表达式，其中，偏振速度的解析表达式以压强场的解析解表示；

步骤2：将空间交错网格差分格式与时间递推格式相结合，带入平面波通解，得到交错时间递推格式；

步骤3：在波数域采用最小二乘迭代求解交错网格差分算子；

步骤4：将优化的差分算子用于声波正演模拟。

进一步，在步骤1中，对一阶压强-速度偏微分方程组的偏微分方程通过在笛卡尔坐标系中利用空间积分变换获得常微分方程；对此常微分方程方程做时间积分得到平面波通解；对方程两边分别做二维空间傅里叶变换和时间积分并省略常数项，得到偏振速度分量的通解；在此，偏振速度的解析表达式通过压强场的解析解表示。

进一步，在步骤2中，交错时间递推格式将时间差分与空间差分结合在一起，带入平面波通解，分别得到时间差分与空间差分在波数域的响应，即将解析解带入空间交错网格差分格式，得到时间差分与空间差分在波数域的精确响应，目标是用等式右边的函数(空间差分滤波响应)在波数域逼近等式左边的(时间差分滤波响应)精确的解，最终实现时间差分与空间差分同时达到高精度。由于偏振速度的解析表达式通过压强场的解析解表示，考虑了时间差分与空间差分两方面的内容，所以所述交错时间递推格式将时间差分与空间差分结合是指将解析解带入空间交错网格差分格式，得到的递推格式即为交错时间递推格式。

进一步，在步骤3中，目标是用等式右边的函数在波数域逼近等式左边精确的解，通过定义目标函数修改匹配系数，使得匹配系数在一定的波数范围内尽可能的逼近精确 时间递推算子；对目标函数方程进行等间隔离散采样，将系数的求取转换为最小二乘优化问题并进行迭代求解，得到高精度交错网格差分算子。

进一步，在步骤3中，将时间交错差分算子波数域响应作为目标函数，并使用空间差分算子波数域响应作为基函数进行最小二乘逼近，问题可归纳为最小二乘优化问题，采用预处理的共轭梯度迭代解法增加解的稳定性。

进一步，在步骤3中，采用最小二乘迭代求解包括：通过交错时间递推格式，在有效波数段求取匹配系数，考虑到系数求解的病态性，采用预处理的共轭梯度迭代算法，以求取最优的匹配系数，在处理变密度介质时，既能较好压制数值频散，同时可以提高群速度精度。

进一步，所述预处理的共轭梯度迭代算法利用一阶声波偏微分方程组解析解将时间差分与空间差分相统一，并使用共轭梯度法在波数域对时间与空间差分算子进行同时优化，能够较为有效地压制数值频散，并在一定程度上提高地震波群速度的计算精度。

进一步，所述匹配系数为在常规的空间交错网格基础上的时间递推匹配系数，可实现时间与空间差分的同时优化。

与现有的处理复杂地表的资料的技术相比，本方法主要有四点优势：

(1)在标准交错网格基础上，提出了一种新的时间递推匹配系数确定方法，该递推方法得到的波场精度较高。

(2)利用一阶声波偏微分方程组解析解将传统的空间交错网格差分格式与精确时间递推格式相结合，使模拟精度在时间与空间两个方面同时得到优化，最终在时间差分与空间差分同时达到高精度，尤其在高阶数情况下可以达到显著的效果。

(3)传统方法采用零附近的泰勒展开求取系数，在低波数范围精度较高，随着波数增加，误差快速增大，为提高精度常采用更高阶的差分格式，这大大增加了计算量。本方法在整个有效波数段同时优化时间差分与空间差分，可以较小的差分阶数，达到相同的精度，从而提高计算效率。

(4)由于真实地下介质既存在速度变化也存在密度的变化，大量事实表明一阶压强-速度方程更加利于处理变密度介质，因此本方法模拟精度更接近真实地下介质。

附图说明

图1是阶数为M＝4情况下t＝1s时刻传统交错网格差分方法模拟得到的波场快照图；

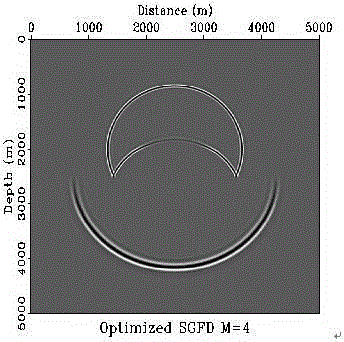
图2分别为在阶数为M＝4情况下t＝1s时刻优化后的差分方法模拟得到的波场快照图；

图3为测试所用的Marmousi2模型速度场；

图4为测试所用的Marmousi2模型密度场；

图5为利用传统正演算法得到的单炮记录；

图6为利用本发明正演模拟得到的单炮记录；

图7为利用传统正演算法得到的单炮记录的局部放大图；

图8为应用发明正演模拟得到的单炮记录局部放大图。

具体实施方式

为使本发明的上述和其他目的、特征和优点能更明显易懂，下文特举出较佳实例，并配合所附图式，作详细说明如下。

实施例1。

针对数值频，可从优化差分系数入手，可进行以下三个方面的改进：(1)基于平面波原理，推导微分算子与差分算子在波数域中的滤波响应；并利用函数拟合算法使差分算子逼近微分算子；(2)在波数域将空间差分与谱分解相结合，改进差分算子减小计算误差。(3)从网格节点方面改进有限差分计算精度。

基于时空域优化的交错网格正演模拟方法可通过如下技术措施来实现：步骤1，速度-压强方程组的平面波解，结果将用于后面精确的交错时间递推格式系数的求取；步骤2，交错网格时间递推格式，目标是用等式右边的函数在波数域逼近等式左边精确的解；步骤3，最小二乘迭代求解。

在步骤1中，考虑二维常密度与常速度情况下，得到一阶压强-速度偏微分方程组,然后通过在笛卡尔坐标系中利用空间积分变换获得常微分方程，对此常微分方程方程做时间积分得到平面波通解，对方程两边分别做二维空间傅里叶变换和时间积分并省略常数项，得到偏振速度分量的通解。在此，偏振速度的解析表达式是通过压强场的解析解表示出来的，该表达式将用于后面精确的交错时间递推格式系数的求取中，这也是本方法的基础所在。

在步骤2中，交错网格相比于常规的规则网格具有更高的模拟精度，首先根据公式得到精确的交错时间递推格式，通过式中傅里叶反变换可实现波场的时间递推，同时该递推方法得到的波场精度较高。然而，正反傅里叶变换带来的巨大的计算量限制了其在偏移成像中的应用。考虑到时空域交错网格有限差分正演模拟计算效率高并兼顾较高的精度，将传统的空间交错网格差分格式与精确时间递推格式相结合，使模拟精度在时间与空间两个方面同时得到优化。得到一种用空间交错差分实现交错时间递推格式，然后 将时间与空间差分进行同时优化。最终在时间差分与空间差分同时达到高精度。

由于偏振速度的解析表达式通过压强场的解析解表示，考虑了时间差分与空间差分两方面的内容，所以所述交错时间递推格式将时间差分与空间差分结合，是指将解析解带入空间交错网格差分格式，得到的递推格式即为交错时间递推格式。空间交错网格差分格式采用现有技术中的交错网格有限差分格式。

在步骤3中，通过定义目标函数修改匹配系数，使得匹配系数在一定的波数范围内尽可能的逼近精确时间递推算子；对目标函数方程进行等间隔离散采样，将系数的求取转换为最小二乘优化问题。考虑到优化问题的病态性与多解性，采用预处理的共轭梯度迭代解法增加解的稳定性。

应用实施。

(1)选取平层模型进行正演模拟，上层速度为1.3km/s，下层速度为3.2km/s；上层密度为1.7g/cm³，下层密度为2.7g/cm³，网格大小为501×501，网格间距为Δx＝Δz＝10m。计算参数为：采用主频为20Hz的雷克子波作为震源，最高频率约为60Hz，震源的网格坐标为(251,201)，计算时间步长设定为1ms。

(2)图1与图2分别为在阶数为M＝4情况下t＝1s时刻传统交错网格差分方法模拟得到的波场快照，优化后的差分方法模拟得到的波场快照，传统方法有模拟结果明显的频散现象，优化后频散得到压制；

(3)选取国际标准Marmousi2模型进行正演模拟测试，该模型横向851个CDP点，纵向467个采样点，纵横向采样间距均为10m，模型速度变化范围为1428m/s到4700m/s，如图3所示；

(4)图4所示为与图3速度模型对应的密度模型，密度变化范围为1.01g/cm³到2.627g/cm³；

(5)正演模拟计算参数为：采用主频为20Hz的雷克子波作为震源，最高频率约为60Hz，计算时间步长为Δt＝1ms；图5和图6分别为传统方法与本发明得到的地震记录，两种方法使用相同的差分阶数M＝4，均使用了PML边界处理方法。

(6)为了更好的比较两种方法的数值模拟结果，图7和图8分别展示了传统方法与本发明得到的地震记录的局部放大图；

对比两种方法的局部放大图(图7和图8)，可以清楚的看到传统方法的正演地震记录有明显的数值频散(图7虚线范围内)，而本发明方法得到的地震记录，数值频散得到 较好的压制(图8虚线范围内)。从而验证了本发明在压制数值频散方面的优势以及对复杂模型的适应性。

从以上的描述中，可以看出，本发明实施例提出了一种新的时间递推匹配系数确定方法；利用一阶声波偏微分方程组解析解将时间差分与空间差分相统一，并使用共轭梯度法在波数域对时间与空间差分算子进行同时优化。本发明在标准交错网格基础上，提出了一种新的时间递推匹配系数确定方法。利用一阶声波偏微分方程组解析解将时间差分与空间差分相统一，并使用共轭梯度法在波数域对时间与空间差分算子进行同时优化，能够较为有效地压制数值频散，并在一定程度上提高地震波群速度的计算精度。采用其它交错网格正演模拟方法尽管也可以实现同样的目的，但其精度和计算效率较低。

以上所述仅为本发明的优选实施例而已，并不用于限制本发明，对于本领域的技术人员来说，本发明实施例可以有各种更改和变化。凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。