一种近实时地震震源位置定位方法与流程

本发明涉及一种地震震源位置定位方法，尤其涉及一种仅利用地震台网中前三个台站的P波到时信息进行近实时地震震源位置定位的方法。

背景技术：
地震定位是地震学中的一个基本问题，其主要任务是精确确定震源位置(震中位置和震源深度)及发震时刻。在地震预警中，对有潜在破坏的大震，快速可靠的定位信息也是决定预警成败的首要问题。作为超级地震速报的地震预警，由于时效性的要求，需要快速可靠的得到地震位置。但目前所用的传统地震定位方法需要较多的震相到时信息，己经难以应用到对时间要求严格的地震预警中去，近实时快速可靠定位是地震预警定位的难点及关键所在。如前所述，为了满足时效性要求，地震预警定位是基于有限信息的近实时定位方法，目前己经发展了多种快速定位方法，主要是采用单台方位角和单台震中距的方法进行地震快速定位。首先，利用了单台地震波形进行递推求取。在P波到达后，用平滑后三分量记录的水平向幅值比和垂直向符号来确定震中方位角，方法大致同传统的单台定位方法中的震中方位角确定方法。再利用统计经验公式求取震中距，最后求取震中距与方位线的交点坐标。认为震级和P波卓越频率有关，得到震级后由初始信息幅值和震级随距离的衰减关系得到震源距，经验认为震中距与震源距的比值及震源深度和震源距的比值与记录初始部分竖直分量与水平分量比值的最大值有明显关系，进而得到震中距和震源深度。此定位方法为经验性方法，而且定位中用到了同样具有较大误差的震中方位角和震级。由目前的定位方法来看，主要是基于部分到时信息的，方法比较单一，信息的利用率较低，时效性差，定位结果的可靠性不高。

技术实现要素：
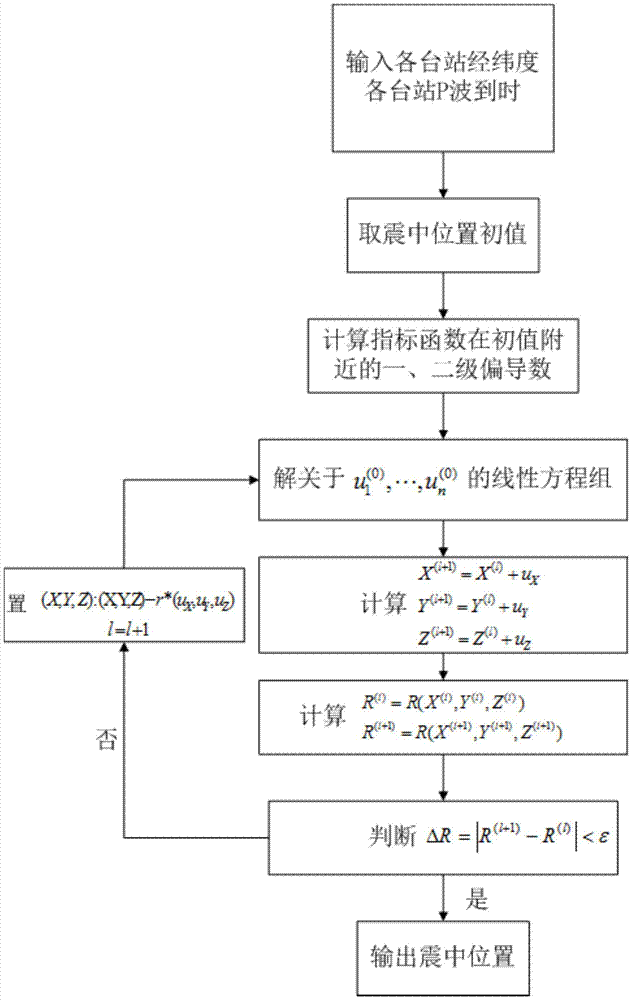
本发明的目的就在于为了解决上述问题而提供一种仅利用地震台网中前三个台站的P波到时信息的近实时地震震源位置定位方法。本发明通过以下技术方案来实现上述目的：一种近实时地震震源位置定位方法，包括以下步骤：步骤一：地震发生后，对于最先得到P波到时的三个台站，读取台站编号和地理坐标，识别P波到时，两两求出到时差，对地震台站的经纬度坐标数据进行投影变换转换成平面直角坐标；步骤二：对任意两个台站，假设某台站S1坐标为(x11，y12)，震相到时为T1，另一台站S2坐标为(x21，y22)，同一震相到时为T2，震中位置为(x0，y0)，震源深度为z0，假定震相波速恒定为Vp，则有：根据区域地壳模型，确定P波波速，台站震相到时己知，假定z0值，则式(1)中的震中位置(x0，y0)为双曲线，由到时的先后顺序，震中位于靠近先到台站的一支上，两两台站相互组合得到三条双曲线，即H12、H13和H23，由于P波捡拾精度的影响，三条双曲线不会交于一点，而是两两相交；步骤三：根据交点坐标构成的三角形，计算三角形重心，该重心的坐标即为震中位置初值；以下步骤四至步骤八为修订震中位置初值，求得震中位置精确解的计算过程：步骤四：采用直角坐标系，P波的走时方程为：其中，xk,yk,zk为台站横纵坐标和震源深度，X，Y，Z为待求得震中位置坐标；O为地震发生时刻；k＝1,2,...,m，且m≥3；步骤五：令其中，xk,yk,zk为台站横纵坐标和震源深度；X，Y，Z为待求得震中位置坐标；令：τ＝VpO(4)根据观测到时和理论到时差建立指标函数：根据多元函数的极值理论，指标函数R的函数值达到极小值的必要条件是：将在初值附近做泰勒展开得到修定方程：其中，i＝1,2,...,n，是初值的修正量，是指标函数在初值附近的二级偏导数，步骤六：将震中位置试探值，第一次迭代时取震中位置初值，第二次迭代开始取前一次迭代过程求得的震中位置试探值，并由此在n次迭代过程中取n-1次求得的震中位置试探值代入式(7)，求解此方程组，可得：其中，i＝1,2,…,n式(9)是fk(X1,X2,...,Xn)＝εk的解的一级近似值，如果：ΔR＝R(1)-R(0)＜ε(10)ε是试验数值即试取的某个小量，则式(9)就是满足要求的最后的解；步骤七：如果不能满足式(10)，则用作为新的试探值，并求出在这个新的点附近的二级偏导数步骤八：重复步骤六和步骤七，直到满足要求为止；步骤九：通过坐标反变换将震中位置转换为经纬度坐标，此坐标即为最终结果。本发明的有益效果在于：本发明利用依据数字地震台网中各台站不同震相到时顺序，针对中国台网现状及今后发展趋势，提出了一个应用于地震预警的近实时定位方法，通过排除震中方位角和震级估算的误差，提高地震定位精度；通过该方法充分应用有限到时信息，针对不同到时信息的特点，从台网中第一个台站至第三台接收到P波的时间段内，利用前三台到时信息，基于双曲线约束和到时残差平方和最小的优化思想，快速给出精度上可接受的震中定位。附图说明图1是本发明实施例中震中位置(x0，y0)的到时差双曲线示意图；图2是本发明所述近实时地震震源位置定位方法的流程图；图3是本发明实施例中震中定位实例结果图。具体实施方式下面结合实施例和附图对本发明作进一步说明：实施例：下面以2015年4月23日的日本某3.8级地震为例，根据三个台站P波信息，进行地震震源位置定位，并与实际信息比对。如图2所示，具体操作步骤如下：步骤一：地震发生后，分别打开最先得到P波到时的前三个地震台即台站的地震加速度记录，读取台站编号AOM0051504232215、AOM0041504232215、AOM0201504232215，以及地理坐标(Lat1，Long1)、(Lat2，Long2)、(Lat3，Long3))，识别P波到时(Time1、Time2)，两两求出到时差，对地震台站的经纬度坐标数据进行投影变换转换成平面直角坐标(x11，x12)、(x21，x22)、(x31，x32)；步骤二：对任意两个台站，假设某台站S1坐标为(x11，y12)，震相到时为T1，另一台站S2坐标为(x21，y22)，同一震相到时为T2，震中位置为(x0，y0)，震源深度为z0，假定震相波速恒定为Vp，则有：根据区域地壳模型，确定P波波速，台站震相到时己知，假定z0值，则式(1)中的震中位置(x0，y0)为双曲线，根据公式(1)画出满足到时差的双曲线，由到时的先后顺序，震中位于靠近先到台站的一支上(如图1所示)，两两台站相互组合得到三条双曲线，即H12、H13和H23，由于P波捡拾精度的影响，三条双曲线不会交于一点，而是两两相交；步骤三：根据交点坐标构成的三角形，计算三角形重心，该重心的坐标即为震中位置初值；步骤四：进一步修订震源位置：采用直角坐标系，P波的走时方程为：其中，k＝1,2,...,m，且m≥3；步骤五：根据观测到时和理论到时差可以建立观测方程和指标函数，对观测方程和指标函数进行“减元”处理：令τ＝VpO(4)根据观测到时和理论到时差建立指标函数：根据多元函数的极值理论，指标函数R的函数值达到极小值的必要条件是：将在初值附近做泰勒展开得到修定方程：其中，i＝1,2,...,n，是初值的修正量，是指标函数在初值附近的二级偏导数，步骤六：求R对X,Y,Z的一、二级偏导数：将式(7)代入震中位置初值，求解此方程组，可得：其中，i＝1,2,…,n式(9)是fk(X1,X2,...,Xn)＝εk的解的一级近似值，如果：ΔR＝R(1)-R(0)＜ε(10)ε是试验数值即试取的某个小量，则式(9)就是满足要求的最后的解；步骤七：如果不能满足式(10)，则用作为新的试探值，并求出在这个新的点附近的二级偏导数步骤八：重复步骤六和七，直到满足要求为止；步骤九：通过坐标反变换将震中位置转换为经纬度坐标，此坐标即为最终结果，台站信息及计算结果和误差如图3所示。上述实施例只是本发明的较佳实施例，并不是对本发明技术方案的限制，只要是不经过创造性劳动即可在上述实施例的基础上实现的技术方案，均应视为落入本发明专利的权利保护范围内。