一种基于GNSS网形变化的形变异常检测方法与流程

本发明属于测绘科学与技术领域，尤其涉及区域微动态形变信息提取和形变异常时空分布检测。

背景技术：

目前，关于GNSS地壳形变信息提取和形变异常检测方面的研究更多的是集中在这三个方面。一是基于GNSS基线长度变化；二是基于GNSS站坐标位移变化；三是基于GNSS位移场求应变。

第一种方法，通过GNSS基线长度变化只能用来分析区域地壳形变的拉张或压缩，且基线方向与形变方向不同，所得结果差异很大。而且对于走滑或旋转形变，基线变化并不明显。

第二种方法，通过GNSS站坐标位移变化虽可观察到每个台站的位移变化，具有直观性，但是位移依赖于基准，使用不同的基准将会得到不同的位移场。同时，基准站参考框架的选择是一个动态的过程，并不是固定不变的，因此需要找到合适的位移参考基准才能反映真实的地壳形变位移特征，而找到合适的位移参考基准不易。

第三种方法，即通过GNSS位移位移场求应变，可以借助应变张量的计算方法得到区域应变场主应变、剪应变、旋转角和面膨胀的动态变化过程，作为反映区域运动、变形性质和强度随时间变化的参数。但前提是假定单元内部介质均匀,位移连续,小变形等。

一个站的位置变化或一个基线长度的变化反映的仅仅是一个点，一个线的形变信息，并不能代表整体的区域形变特征。而且，若这个点或线形变量表现的很小，那么就难以发现整体区域的微动态形变。同时，从长期连续观测、庞大的GNSS网络中逐期逐站、地毯式筛选的方法检测形变异常信息将会十分耗时，效率很低。

为此，提出了一种利用不受框架和共模噪声影响、相对精度较高GNSS网形变化来检测地壳形变异常的方法。

技术实现要素：

本发明的目的是提供一种基于GNSS网形变化的形变异常检测方法，能够快速获取形变异常的时空分布信息。

为达到上述目的，本发明采用的技术方案是：一种基于GNSS网形变化的形变异常检测方法，包括以下步骤：

1)、将检测区域的长期连续观测的GNSS测站组建GNSS时空监测网络；

2)、对各期GNSS监测网进行基线解算和三维无约束自由网平差；

3)、将平差后的GNSS网进行高斯投影得到一个平面的网形及各站点平面坐标；

4)、利用第一期观测网中的一站点坐标作为参考位置，将此点与另一站点构成基线的方向作为参考方向，将其它各期观测的GNSS网进行平移和旋转变换。使每期的网形都统一到一个固定点和一个固定的参考方向上，并得到网中所有测站转换后的坐标；

5)、利用转换后的坐标求取整个GNSS时空监测网络所有基线长度、基线夹角、基线方位角和所有测站位移四个的要素的时空变化序列，作为衡量网形变化的指标；

6)、构建这四要素时空矩阵，进行主成分时空响应分析；

7)、确定形变异常时空分布及演变特征。

所述的步骤4)具体为：设构建的GNSS时空监测网络测站数为m个，观测总期数为n期，选择的第一期参考站坐标为(x₀,y₀)，参考基线边的坐标方位角为α₀，则各期GNSS时空监测网络所有站坐标经平移旋转变换后的新坐标为：

上式中，i表示测站号，取值为i＝1……m；j表示观测期数，取值为j＝1……n。

所述的步骤(5)中利用转换后的坐标求取整个GNSS网所有基线长度、基线夹角、基线方位角和所有测站位移，具体如下所述：

测站i与测站i+1构成的平面基线向量为：

则测站i与测站i+1构成的基线长度为：

基线i～i+1与基线i～i+2之间的夹角为：

基线i～i+1的方位角为：

测站i位移为：

所述的步骤(6)具体包括：

61)、设时空序列矩阵为X_m×n，其中，每一行代表一个测站位移、一条基线长度、一个基线方位角或基线夹角所有期的变化值；每一列表示一期所有测站位移、基线长度、基线方位角或基线夹角的变化值；

62)、为保证所有变化时间序列都是以零为基点，按式(10)对矩阵X_m×n中每一元素实施中心化：

式中，i,j表示矩阵的行列号，i＝1,2…m；j＝1,2…n；

63)、对中心化后的矩阵X'_m×n进行奇异值分解，得到正交矩阵U_m×m、V_n×n和由奇异值构成的矩阵S_m×n，表示为：

X'_m×n＝U_m×mS_m×nV_n×n^T (11)；

64)、将奇异值从大到小排列，前几个模式分量之和称为主模式分量，它包含了原序列的大部分信息；若取前r个为主模式，则矩阵X'_m×n近似表示为：

X_m×n'≈X'_r＝U_rS_rV_r^T (12)

式中，S_r为S_m×n中前r个较大奇异值组成的对角阵，V_r为V_n×n中对应前r个列向量组成的矩阵，其中的每一列称为时间主模式向量；U_r为U_m×m中对应前r个列向量组成的矩阵，其中的每一列称为空间主模式向量。

所述的步骤(7)具体包括：

71)、根据时间主模式向量得到时间响应曲线，分析区域形变随时间的动态变化特征；根据空间主模式向量得到空间响应图，分析区域形变对GNSS网中不同测站的不同影响程度；

72)、从时间响应曲线是否呈均匀线性变化来判断形变异常发生的时间，若曲线偏离原来的线性趋势，或呈现非线性、非均匀变化或有剧烈的震荡，则表明这一时间段内极有可能发生了形变异常；

从空间响应图中各测站空间响应的大小来判断形变发生的空间分布,空间响应较大的测站受形变影响较大，说明距离形变发生的区域范围较近；反之，空间响应较小的测站受形变影响较小，说明距离形变发生区域较远，由此判断形变发生的区域范围。

本发明具有的优点如下所述：

本发明针对GNSS三维无约束自由网平差不依赖基准且拥有高精度几何网形的特点，利用整个GNSS网所有测站间相互关联的观测数据构建了衡量整个网形变化的指标体系。用网形的变化集中突出了整个区域的地壳形变信息。利用地壳形变高空间相关性的特点，通过主成分时空响应分析的方法实现了区域地壳形变时空信息的快速提取。试验表明，采用网形的变化具有一定的捕捉微弱形变信息能力，有利于地壳微动态形变异常信息的检测。

附图说明

图1为本发明的方法流程图；

图2为GNSS网基线长度变化的时间响应曲线图；

图3为GNSS网基线夹角变化的时间响应曲线图；

图4为GNSS网基线长度变化的空间响应图；

图5为GNSS网基线夹角变化的空间响应图。

具体实施方式

如图1所示，本发明公开了一种基于GNSS网形变化的形变异常检测方法，GNSS的全称是全球导航卫星系统(Global Navigation Satellite System)，它是泛指所有的卫星导航系统，包括全球的、区域的和增强的，如美国的GPS、俄罗斯的Glonass、欧洲的Galileo、中国的北斗卫星导航系统。此处以GPS网为例进行说明，具体包括以下步骤：

1)、将检测区域长期连续观测的GPS测站构成区域GPS时空监测网络。

2)、对GPS时空监测网络进行基线解算和三维无约束自由网平差；其中基线解算和三维无约束自由网平差为现有的计算方法，在此不再进行详细说明。

3)、对三维无约束自由网平差后的GPS时空监测网络进行高斯平面投影得到GPS网的一个平面的网形及各站点平面坐标；此处所述的高斯平面投影为现有的方法，不再赘述。

4)、在各站点平面坐标中利用第一期观测到的任一站的坐标作为参考位置，将此站与另一站构成基线的方向作为参考方向，把后面每期观测到的GPS网的平面坐标在高斯平面上进行平移和旋转变换，使每期的网形都统一到一个固定点和一个固定的参考方向上，从而得到转换后的坐标。具体如下所述：

设构建的GPS网测站数为m个，观测总期数为n期，选择的第一期参考站坐标为(x₀,y₀)，参考基线边的坐标方位角为α₀，则各期GPS网所有站坐标经平移旋转变换后的新坐标为：

式中，i表示测站号，取值为i＝1……m；j表示观测期数，取值为j＝1……n。

5)、利用转换后的坐标求取整个GPS网所有基线长度、基线夹角、基线方位角和所有测站位移，作为衡量GPS网形变化的四个指标。具体计算公式如下所述：

测站i与测站i+1构成的平面基线向量为：

则测站i与测站i+1构成的基线长度为：

基线i～i+1与基线i～i+2之间的夹角为：

基线i～i+1的方位角为：

测站i位移为：

6)、构建时空序列矩阵，进行主成分时空响应分析；具体包括如下步骤：61)、设时空序列矩阵为X_m×n，其中，每一行代表一个测站位移、一条基线长度、一个基线方位角或基线夹角所有期的变化值；每一列表示一期所有测站位移、基线长度、基线方位角或基线夹角的变化值；即若每一行表示一个测站位移所有期的变化值，则每一列表示一期所有测站位移的变化值；

62)、为保证所有变化时间序列都是以零为基点，按式(10)对矩阵X_m×n中每一元素实施中心化：

式中，i,j表示矩阵的行列号，i＝1,2…m；j＝1,2…n；

63)、对中心化后的矩阵X'_m×n进行奇异值分解，得到正交矩阵U_m×m、V_n×n和由奇异值构成的矩阵S_m×n，表示为：

X'_m×n＝U_m×mS_m×nV_n×n^T (11)

64)、奇异值的大小反映了主成分时空模式分量对时间序列贡献率的大小，将奇异值从大到小排列，前几个模式分量之和称为主模式分量(一般取第一主成分)，它包含了原序列的大部分信息；若取前r个为主模式，则矩阵X'_m×n近似表示为：

X_m×n'≈X'_r＝U_rS_rV_r^T (12)

式中，S_r为S_m×n中前r个较大奇异值组成的对角阵，V_r为V_n×n中对应前r个列向量组成的矩阵，其中的每一列称为时间主模式向量；U_r为U_m×m中对应前r个列向量组成的矩阵，其中的每一列称为空间主模式向量，反映了整个时间序列中各站形变的响应大小。

7)、提取形变异常时间分布和形变异常空间分布：当利用主成分分解得到时空主模式向量之后，用时间主模式向量反映区域形变随时间的变化过程；用空间主模式向量反映区域形变对GPS网中所有测站的影响程度，具体如下所述：

71)、根据时间主模式向量得到时间响应曲线，分析区域形变随时间的动态变化特征；根据空间主模式向量得到空间响应图，分析区域形变对GPS网中各测站的的不同影响程度；

72)、从时间响应曲线是否呈均匀线性变化来判断形变异常发生的时间，若曲线偏离原来的线性趋势，或呈现非线性、非均匀变化或有剧烈的震荡，则表明这一时间段内极有可能发生了形变异常；从各测站空间响应的大小来判断形变发生的空间分布,空间响应较大的测站受形变影响较大，说明距离形变发生的区域范围较近；反之，空间响应较小的测站受形变影响较小，说明距离形变发生区域较远，由此判断形变发生的区域范围。

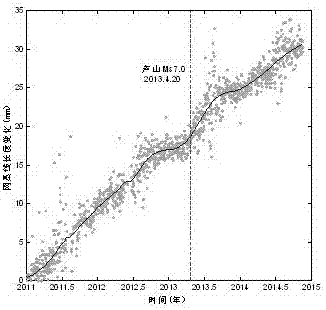
以2013年芦山Ms7.0地震发生的地壳形变为例，采用本发明所述方法提取GNSS网所有基线长度与基线间夹角的单日解时空变化序列时间响应分别见图2和图3。由图2所示，基线长度变化趋势整体处于线性增加状态，在震前曾出现了一度闭锁状态，但并不十分明显。相对基线长度变化，图3所反映的基线夹角变化在震前形变表现的更加突出，可以明显看出约在震前9个月(2012年6月左右)开始出现了较大的波动，偏离了之前线性变化的趋势。提取GNSS网基线长度和基线夹角变化的PC1空间响应特征见图4和图5。图中不同颜色表示不同的空间响应程度，正值代表增大，负值代表减小。由图4所示，基线SCXJ-SCLH压缩量相对较大，占23％；其次是基线SCXJ-SCMB和SCDF-SCSM，占15％和16％。基线SCXJ-SCYX和基线SCXJ-SCSM处于扩张状态，各占16％和12％；其它响应程度较小，低于9％。总的来说，与测站SCXJ相关的基线长度变化相对较大。而测站SCXJ正是距离震中最近的一站。由图5所示的基线夹角变化的空间响应看，与测站SCXJ、SCMB相关的夹角变化的空间响应程度较大，分别为-20％和27％。可见，角度形变主要发生在GNSS网的东部区域，这与震中位置相吻合。

由此可知，本发明能够得到区域地壳形变时空分布特征及形变的动态演变过程，有利于微动态形变信息的提取和形变异常信息的检测。

本发明将研究区域的GNSS测站组建GNSS网，进行三维无约束自由平差，将坐标结果转换到高斯平面。并以网中一个点和一个边作为参考位置和参考方向，对GNSS网进行了网形的旋转和平移变换。因三维无约束自由网平差结果虽每期坐标框架浮动较大，但GNSS几何网形结构不变；且不受共模误差和不相关噪声的影响，相对位置精度较高。它所确定的观测点位几何形状只取决于观测数据的质量；利用整个GNSS网形的变化分析能够有效分离不相关噪声的影响，集中突出了高空间相关的形变信息，具有一定的捕捉微形变信息能力。

根据区域形变信息高空间相关性的特点，以GNSS网形作为研究单元，分别从GNSS网所有基线长度变化、基线间夹角变化、基线方位角变化和所有站水平位移时间序列四个方面综合构建了衡量整个网形变化的指标体系。通过这四个方面的主成分时空响应得到区域地壳形变时空分布特征和动态演变过程。研究结果表明，该方法更利于微动态形变信息的提取和形变异常检测。这为形变监测及其动力学机制探索提供了一定的理论基础和参考依据。