一种实现位同步的方法和装置与流程

本文涉及但不限于导航技术，尤指一种实现位同步的方法和装置。

背景技术：

全球定位系统(globalpositioningsystem)接收机在完成对接收到的信号的捕获后，在跟踪接收到的信号的同时，对接收到的信号进行位同步、帧同步和解调解码，从而从接收到的信号中获得信号的发射时间和导航电文，并最终实现gps导航定位。

其中，位同步又叫比特同步，即接收机根据一定的算法确定接收到的信号的比特起始位。对于调制在相应载波上的50比特每秒(bps，bitspersecond)的导航电文，每个导航电文对应20个c/a码周期(即1比特数据)，每个c/a码周期包括1毫秒(ms)的信号段，相邻两个导航电文之间的分界点为比特翻转边界。比特同步即是要获得导航电文的比特翻转边界的位置，它是实现解调导航电文、测量伪距和实现高灵敏跟踪的基础。因此，接收机必须估计出比特翻转边界的位置，即实现位同步。

相关的实现位同步的方法包括直方图法、最大似然(ml，maximumlikelihood)法等。

接收机对接收到的信号与生成的c/a码进行相关，相关后的信号分别与生成的i路本地载波信号和q路本地载波信号进行混频得到i路混频后的信号和q路混频后的信号，分别将1毫秒(ms)的i路混频后的信号和1ms的q路混频后的信号进行积分得到i路积分后的信号和q路积分后的信号。直方图法即是对i路积分后的信号或q路积分后的信号进行处理。

其中，图1为直方图法的示意图，如图1所示，直方图法是一种相当基本的位同步算法。该方法以20个积分后的信号(一个积分后的信号由一个1ms的混频后的信号进行积分得到)为周期对20个候选位置进行符号变化的 统计，每一个候选位置对应一个计数器，当第i个积分后的信号到第(i+1)个积分后的信号符号发生改变时，第(i+1)个积分后的信号对应的候选位置对应的计数器加1；当第i个积分后的信号到第(i+1)个积分后的信号符号未发生改变时，不将第(i+1)个积分后的信号对应的候选位置对应的计数器加1。

每当统计完20个积分后的信号，判断20个计数器中是否有一个计数器达到门限n1，如果有，则该计数器对应的候选位置即为比特翻转边界。图1中第4个候选位置对应的计数器达到门限n1，则第4个候选位置即为比特翻转边界。即1～3ms的信号属于一个比特，4～23ms的信号属于下一个比特。

如果20个计数器中至少有两个计数器达到门限n2，则将20个计数器清零，重新进行位同步。

直方图法本质上是对积分后的信号进行硬判决，然后考察相邻两个c/a码周期的符号是否发生变化来实现位同步，其缺点就是随着积分后的信号强度变弱，其性能会变得越来越差，同步所需要的时间也会越来越长。

其中，ml法是把每个候选位置之后的连续20个积分后的信号进行累加，求累加后的信号的比特能量，再把比特能量进行一段时间的非相干累加，这样对应20个候选位置中非相干累加结果最大的候选位置即为比特翻转边界。

假设接收机在第k个历元时(即1ms)接收到的信号积分后的模型如公式(1)所示。

rk＝abk+nk(1)

其中，k为历元时，rk为第k个历元时积分后的信号，a为信号功率，bk为第k个历元时假设的积分后的信号，nk为第k个历元时均值为0，方差为的加性高斯白噪声。

一个包含了n个积分后的信号的矢量的似然函数可以由每个相关后的信号的似然函数之积来表示，如公式(2)。

其中，bk为第k历元时假设的积分后的信号，δ为候选比特翻转边界，为向下取整，σ0为噪声方差，n为积分后的信号的个数，a为信号功率。

要想找到比特翻转边界，公式(2)需要在δ，a，b为变量下的最大化。显然，公式(2)中第一项与变量δ，a，b无关，可以被忽略。后两项可以看成2｜a｜f(r,δ,b)+n｜a｜²，因此，要实现公式(2)的最大化，只要将f(r,δ,b)最大化即可，其中，

其中，k＝n/20+1。

通过观察不难发现，当bk与符号相等时，公式(3)达到最大值。根据公式x·sign(x)＝|x|，公式(3)的最大化等价于公式(4)的最大化。

于是，最大似然法可归结为采用公式(5)获得比特翻转边界。

其中，为比特翻转边界。

ml法只需要几秒的时间就可以在20分贝-赫兹(db-hz)以上的信号强度下获得良好的位同步效果。该方法通常需要固定一个较长的数据段，以保证低信噪比的情况下的同步性能，但对于一个固定长度的数据段，如果该数据段很长，这就相应地会要求存储容量大，提高了处理复杂度，并处理时间较长，得不到实时处理。

技术实现要素：

本发明实施例提出了一种实现位同步的方法和装置，能够降低处理复杂度，缩短处理时间，从而得到实时处理。

本发明实施例提出了一种实现位同步的方法，包括：

计算用于确定比特翻转边界的n个积分后的信号与矩形序列的循环卷积序列；其中，n为大于或等于1的整数；

根据循环卷积序列计算每一个候选位置的能量值；

根据所有候选位置的能量值确定比特翻转边界。

可选的，所述n为20的整数倍，所述矩形序列为长度为20，幅值为1的序列。

可选的，所述计算用于确定比特翻转边界的n个积分后的信号与矩形序列的循环卷积序列包括：

按照公式计算所述循环卷积序列；

其中，y(n1)为所述循环卷积序列的第n1个元素，rl为第l个积分后的信号。

可选的，所述根据循环卷积序列计算每一个候选位置的能量值包括：

按照公式计算第[(δ+1)％20]个候选位置的能量值；

其中，y(20k+δ)为所述循环卷积序列的第(20k+δ)个元素，cc[(δ+1)％20]为第[(δ+1)％20]个候选位置的能量值。

可选的，所述根据所有候选位置的能量值确定比特翻转边界包括：

确定出能量值最大对应的候选位置为所述比特翻转边界。

本发明实施例还提出了一种实现位同步的方法，包括：

计算数据分段与矩形序列的循环卷积序列；继续计算下一个数据分段与矩形序列的循环卷积序列，直到所有数据分段的长度为n；其中，n为大于或等于1的整数；

根据所有数据分段与矩形序列的循环卷积序列计算每一个候选位置的能量值；

根据所有候选位置的能量值确定比特翻转边界。

可选的，所述n为20的整数倍，所述矩形序列为长度为20，幅值为1的序列，每一个所述数据分段的长度为20的整数倍。

可选的，所述计算数据分段与矩形序列的循环卷积序列包括：

按照公式计算第m个数据分段与矩形序列的循环卷积序列；

其中，m为第m个数据分段中所述积分后的信号的个数，rl为第l个积分后的信号，ym(n2)为所述第m个数据分段与所述矩形序列的循环卷积序列的第n2个元素。

可选的，所述根据所有数据分段与矩形序列的循环卷积序列计算每一个候选位置的能量值包括：

按照公式

计算第[(δ+1)％20]个候选位置的能量值；

其中，cc[(δ+1)％20]为所述第[(δ+1)％20]个候选位置的能量值，y0(δ+20l)为第0个数据分段与所述矩形序列的循环卷积序列的第(δ+20l)个元素，ym(δ+(m+1)m)为所述第m个数据分段与所述矩形序列的循环卷积序列的第(δ+(m+1)m)个元素，ym+1(δ+(m+1)m)为所述第(m+1)个数据分段与 所述矩形序列的循环卷积序列的第(δ+(m+1)m)个元素，ynm-1(δ+20l+n)为第(n/m-1)个数据分段与所述矩形序列的循环卷积序列的第(δ+20l+n)个元素。

可选的，所述根据所有候选位置的能量值确定比特翻转边界包括：

确定出所述能量值最大对应的候选位置为所述比特翻转边界。

本发明实施例还提出了一种实现位同步的装置，包括：

第一计算模块，用于计算用于确定比特翻转边界的n个积分后的信号与矩形序列的循环卷积序列；其中，n为大于或等于1的整数；根据循环卷积序列计算每一个候选位置的能量值；

第一确定模块，用于根据所有候选位置的循环卷积确定比特翻转边界。

可选的，所述第一计算模块具体用于采用以下方式实现计算用于确定比特翻转边界的n个积分后的信号与矩形序列的循环卷积序列：

按照公式计算所述循环卷积序列；

其中，y(n1)为所述循环卷积序列的第n1个元素，rl为第l个积分后的信号。

可选的，所述第一计算模块具体用于采用以下方式实现所述根据循环卷积序列计算每一个候选位置的能量值包括：

按照公式计算第[(δ+1)％20]个候选位置的能量值；

其中，y(20k+δ)为所述循环卷积序列的第(20k+δ)个元素，cc[(δ+1)％20]为第[(δ+1)％20]个候选位置的能量值。

可选的，所述第一确定模块具体用于：

确定出能量值最大对应的候选位置为所述比特翻转边界。

本发明实施例还提出了一种实现位同步的装置，包括：

第二计算模块，用于计算数据分段与矩形序列的循环卷积序列；继续计算下一个数据分段与矩形序列的循环卷积序列，直到所有数据分段的长度为n；其中，n为大于或等于1的整数；

第三计算模块，用于根据所有数据分段与矩形序列的循环卷积序列计算每一个候选位置的能量值；

第二确定模块，用于根据所有候选位置的能量值确定比特翻转边界。

可选的，所述第二计算模块具体用于：

按照公式计算第m个数据分段与矩形序列的循环卷积序列；

其中，m为第m个数据分段中所述积分后的信号的个数，rl为第l个积分后的信号，ym(n2)为所述第m个数据分段与所述矩形序列的循环卷积序列的第n2个元素。

可选的，所述第三计算模块具体用于：

按照公式

计算第[(δ+1)％20]个候选位置的能量值；

其中，cc[(δ+1)％20]为所述第[(δ+1)％20]个候选位置的能量值，y0(δ+20l)为第0个数据分段与所述矩形序列的循环卷积序列的第(δ+20l)个元素，ym(δ+(m+1)m)为所述第m个数据分段与所述矩形序列的循环卷积序列的第(δ+(m+1)m)个元素，ym+1(δ+(m+1)m)为所述第(m+1)个数据分段与 所述矩形序列的循环卷积序列的第(δ+(m+1)m)个元素，ynm-1(δ+20l+n)为第(n/m-1)个数据分段与所述矩形序列的循环卷积序列的第(δ+20l+n)个元素。

可选的，第二确定模块具体用于：

确定出所述能量值最大对应的候选位置为所述比特翻转边界。

与相关技术相比，本发明实施例的技术方案包括：计算用于确定比特翻转边界的n个积分后的信号与矩形序列的循环卷积序列；其中，n为大于或等于1的整数；根据循环卷积序列计算每一个候选位置的能量值；根据所有候选位置的能量值确定比特翻转边界。通过本发明实施例的方案，通过计算用于确定比特翻转边界的n个积分后的信号与矩形序列的循环卷积序列来计算每一个候选位置的能量值，从而确定比特翻转边界，由于循环卷积序列可以采用快速傅氏变换(fft，fastfouriertransformation)和快速傅里叶逆变换(ifft，inversefastfouriertransform)来实现，提高了运算速度，缩短了处理时间。

本发明实施例的技术方案还包括：计算数据分段与矩形序列的循环卷积序列；继续计算下一个数据分段与矩形序列的循环卷积序列，直到所有数据分段的长度为n；其中，n为大于或等于1的整数；根据所有数据分段与矩形序列的循环卷积序列计算每一个候选位置的能量值；根据所有候选位置的能量值确定比特翻转边界。通过本发明实施例的方案，将n个积分后的信号划分为多个数据分段，单独计算每一个数据分段与矩形序列的循环卷积序列，而不需要存储n个积分后的信号，只需要存储每一个数据分段，减少了存储容量，降低了处理复杂度，从而得到了实时处理。

附图说明

下面对本发明实施例中的附图进行说明，实施例中的附图是用于对本发明的进一步理解，与说明书一起用于解释本发明，并不构成对本发明保护范围的限制。

图1为相关技术直方图法的示意图；

图2为本发明实施例实现位同步的方法的流程图；

图3为本发明实施例另一实现位同步的方法的流程图；

图4为本发明实施例实现位同步的装置的结构组成示意图；

图5为本发明实施例另一实现位同步的装置的结构组成示意图。

具体实施方式

为了便于本领域技术人员的理解，下面结合附图对本发明作进一步的描述，并不能用来限制本发明的保护范围。需要说明的是，在不冲突的情况下，本申请中的实施例及实施例中的各种方式可以相互组合。

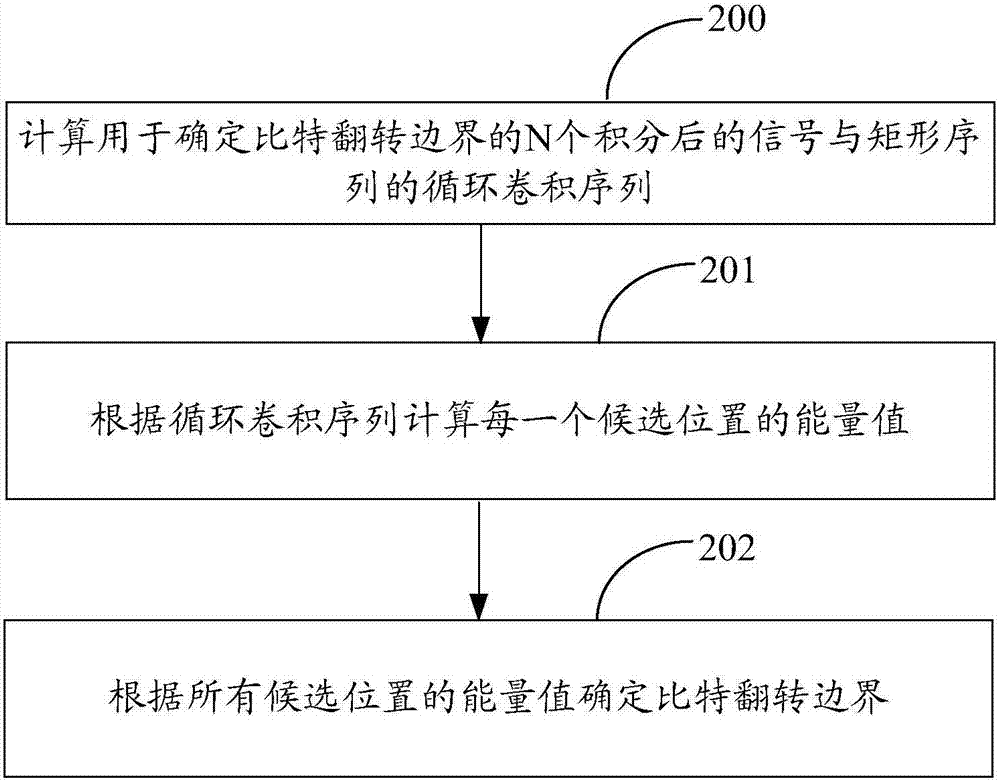
参见图2，本发明实施例提出了一种实现位同步的方法，包括：

步骤200、计算用于确定比特翻转边界的n个积分后的信号与矩形序列的循环卷积序列。

本步骤中，n为大于或等于1的整数。

可选的，n为20的整数倍，矩形序列为长度为20，幅值为1的序列。

其中，矩形序列d为比特的长度(如20ms)。

本步骤中，计算用于确定比特翻转边界的n个积分后的信号与矩形序列的循环卷积序列包括：

按照公式(6)计算循环卷积序列。

其中，y(n1)为循环卷积序列的第n1个元素，rl为第l个积分后的信号。步骤201、根据循环卷积序列计算每一个候选位置的能量值。包括：

按照公式(7)计算第[(δ+1)％20]个候选位置的能量值；

其中，y(20k+δ)为循环卷积序列的第(20k+δ)个元素，cc[(δ+1)％20]为第[(δ+1)％20]个候选位置的能量值。

步骤202、根据所有候选位置的能量值确定比特翻转边界。

本步骤中，根据所有候选位置的能量值确定比特翻转边界包括：

确定出能量值最大对应的候选位置为比特翻转边界。

参见图3，本发明实施例还提出了一种实现位同步的方法，包括：

步骤300、计算数据分段与矩形序列的循环卷积序列；继续计算下一个数据分段与矩形序列的循环卷积序列，直到所有数据分段的长度为n。

本步骤中，n为大于或等于1的整数。

可选的，n为20的整数倍，矩形序列为长度为20，幅值为1的序列，每一个数据分段的长度为20的整数倍。

本步骤中，按照公式(8)计算第m个数据分段与矩形序列的循环卷积序列。

其中，m为第m个数据分段中积分后的信号的个数，rl为第l个积分后的信号，ym(n2)为第m个数据分段与矩形序列的循环卷积序列的第n2个元素。

n2取其他值时，ym(n2)＝0。

步骤301、根据所有数据分段与矩形序列的循环卷积序列计算每一个候选位置的能量值。包括：

按照公式(9)计算第[(δ+1)％20]个候选位置的能量值。

其中，cc[(δ+1)％20]为第[(δ+1)％20]个候选位置的能量值，y0(δ+20l)为第0个数据分段与矩形序列的循环卷积序列的第(δ+20l)个元素，ym(δ+(m+1)m)为第m个数据分段与矩形序列的循环卷积序列的第(δ+(m+1)m)个元素，ym+1(δ+(m+1)m)为第(m+1)个数据分段与矩形序列的循环卷积序列的第(δ+(m+1)m)个元素，yn/m-1(δ+20l+n)为第(n/m-1)个数据分段与矩形序列的循环卷积序列的第(δ+20l+n)个元素。

步骤302、根据所有候选位置的能量值确定比特翻转边界。包括：

确定出能量值最大对应的候选位置为比特翻转边界。

为了更好地对上述方法进行说明，下面以n＝60，m＝20为例进行一个阐述：

首先，分别计算3(n/m)个数据分段与矩形序列的循环卷积序列，其中，

r0(n)＝(r0,r1,…,r19)，r1(n)＝(r20,r21,…,r39)，r2(n)＝(r40,r41,…,r59)为三个数据分段的积分后的信号，每一个数据分段包括20个积分后的信号。

接着，根据时间顺序依次计算每一个数据分段与矩形序列的循环卷积序列y0(n2)，y1(n2)，y2(n2)。

其中，

即y0(0)＝r0，y0(1)＝r0+r1，y0(2)＝r0+r1+r2，……，y0(18)＝r0+r1+r2+…r18；

y0(19)＝r0+r1+r2+…+r19，y0(20)＝r1+r2+…+r19，y0(21)＝r2+r3+…+r19，……，y0(38)＝r19。

即y1(20)＝r20，y1(21)＝r20+r21，y1(22)＝r20+r21+r22，……，y1(38)＝r20+r21+r22+…+r38；

y1(39)＝r20+r21+r22+…+r39，y1(40)＝r21+r22+…+r39，y1(41)＝r22+r23+…+r39，……，y1(58)＝r39。

即y2(40)＝r40，y2(41)＝r40+r41，y2(42)＝r40+r41+r42，……，y2(58)＝r40+r41+r42+…+r58；

y2(59)＝r40+r41+r42+…+r59，y2(60)＝r41+r42+r43+…+r59，y2(61)＝r42+r43+r44+…+r59，……，y2(78)＝r39。

然后计算每一个候选位置的能量值，即

那么，

cc0＝|y0(19)+|y0(19+20)+y1(19+20)|+|y1(19+40)+y2(19+40)|+|y2(19+60)

cc1＝|y0(0)|+|y0(20)+y1(20)+|y1(40)+y2(40)|+|y2(60)

cc2＝|y0(1)|+|y0(1+20)+y1(1+20)|+|y1(1+40)+y2(1+40)|+|y2(1+60)|

cc3＝|y0(2)|+|y0(2+20)+y1(2+20)|+|y1(2+40)+y2(2+40)|+|y2(2+60)|

cc4＝|y0(3)|+|y0(3+20)+y1(3+20)|+|y1(3+40)+y2(3+40)|+|y2(3+60)|

cc5＝|y0(4)|+|y0(4+20)+y1(4+20)|+|y1(4+40)+y2(4+40)|+|y2(4+60)| cc6＝|y0(5)|+|y0(5+20)+y1(5+20)|+|y1(5+40)+y2(5+40)+|y2(5+60)|cc7＝|y0(6)|+|y0(6+20)+y1(6+20)|+|y1(6+40)+y2(6+40)|+|y2(6+60)……

cc19＝|y0(18)+|y0(18+20)+y1(18+20)|+|y1(18+40)+y2(18+40)|+|y2(18+60)|

最后，确定出能量值最大对应的候选位置为比特翻转边界。。

这种方法采用了边输入边计算边输出的方式，不要求大的存储容量，并且其运算量和处理时延也大大减少了。如果处理的运算速度快的话，可实现实时处理。

参见图4，本发明实施例还提出了一种实现位同步的装置，包括：

第一计算模块，用于计算用于确定比特翻转边界的n个积分后的信号与矩形序列的循环卷积序列；其中，n为大于或等于1的整数；根据循环卷积序列计算每一个候选位置的能量值；

第一确定模块，用于根据所有候选位置的循环卷积确定比特翻转边界。

本发明实施例的装置中，第一计算模块具体用于采用以下方式实现计算用于确定比特翻转边界的n个积分后的信号与矩形序列的循环卷积序列：

按照公式计算循环卷积序列；

其中，y(n1)为循环卷积序列的第n1个元素，rl为第l个积分后的信号。

本发明实施例的装置中，第一计算模块具体用于采用以下方式实现根据循环卷积序列计算每一个候选位置的能量值包括：

按照公式计算第[(δ+1)％20]个候选位置的能量值；

其中，y(20k+δ)为循环卷积序列的第(20k+δ)个元素，cc[(δ+1)％20]为第[(δ+1)％20]个候选位置的能量值。

本发明实施例的装置中，第一确定模块具体用于：

确定出能量值最大对应的候选位置为比特翻转边界。

参见图5，本发明实施例还提出了一种实现位同步的装置，包括：

第二计算模块，用于计算数据分段与矩形序列的循环卷积序列；继续计算下一个数据分段与矩形序列的循环卷积序列，直到所有数据分段的长度为n；其中，n为大于或等于1的整数；

第三计算模块，用于根据所有数据分段与矩形序列的循环卷积序列计算每一个候选位置的能量值；

第二确定模块，用于根据所有候选位置的能量值确定比特翻转边界。

本发明实施例的装置中，第二计算模块具体用于：

按照公式计算第m个数据分段与矩形序列的循环卷积序列；

其中，m为第m个数据分段中积分后的信号的个数，rl为第l个积分后的信号，ym(n2)为第m个数据分段与矩形序列的循环卷积序列的第n2个元素。

本发明实施例的装置中，第三计算模块具体用于：

按照公式

计算第[(δ+1)％20]个候选位置的能量值；

其中，cc[(δ+1)％20]为第[(δ+1)％20]个候选位置的能量值，y0(δ+20l)为第0个数据分段与矩形序列的循环卷积序列的第(δ+20l)个元素，ym(δ+(m+1)m)为第m个数据分段与矩形序列的循环卷积序列的第(δ+(m+1)m)个元素，ym+1(δ+(m+1)m)为第(m+1)个数据分段与矩形序列的循环卷积序列的第(δ+(m+1)m)个元素，yn/m-1(δ+20l+n)为第(n/m-1)个数据分段与矩形序列的循环卷积序列的第(δ+20l+n)个元素。

本发明实施例的装置中，第二确定模块具体用于：

确定出能量值最大对应的候选位置为比特翻转边界。

需要说明的是，以上所述的实施例仅是为了便于本领域的技术人员理解而已，并不用于限制本发明的保护范围，在不脱离本发明的发明构思的前提下，本领域技术人员对本发明所做出的任何显而易见的替换和改进等均在本发明的保护范围之内。