模拟微地震的弹性波正演方法与流程

本发明涉及油田开发
技术领域：
，特别是涉及到一种模拟微地震的弹性波正演方法。
背景技术：
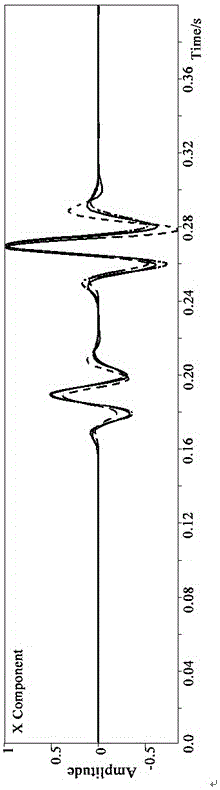
：进入21世纪以来，非常规油气资源表现出巨大的开发潜力。在众多非常规油气的勘探和开发方法中，微地震监测技术起着举足轻重的作用。为了充分掌握微地震技术，需要对微地震的正问题、震源机制进行深入的了解和研究，而实现这一目标最便捷的途径便是地震波数值模拟技术。常规的地震正演技术使用地震子波作为震源，仅适合常规地震勘探的爆炸震源或可控震源，而不能很好的对微地震震源进行描述。目前微地震正演模拟的一种主要方式是基于射线理论，在给点介质模型和震源位置前提下通过射线追踪方式得到微地震记录。但射线理论下模拟的微地震记录无法再现不同频率成分对介质的不同的响应，记录中缺少首波信息，且只能适用于光滑介质。不仅如此，实际中观测到的微地震源具有很宽的频带范围且依赖于介质的变化情况，因此高频射线的假设严重影响了微地震数值模拟的适用范围。另一种方式基于波动理论，使用天然地震的矩张量对岩石破裂模式进行刻画，并使用Green函数法进行弹性波传播数值模拟。但Green函数法求取过程中需要多次求取格林函数，计算量较大，且求取格林函数需要对其进行近似展开，这样就降低了模拟的精度。为此我们发明了一种新的模拟微地震的弹性波正演方法，解决了以上技术问题。技术实现要素：本发明的目的是提供一种引入天然地震中描述刻画震源的矩张量概念，实现对压裂震源的刻画的模拟微地震的弹性波正演方法。本发明的目的可通过如下技术措施来实现：模拟微地震的弹性波正演方法，该模拟微地震的弹性波正演方法包括：步骤1，根据地质勘测的实际资料，分析岩石的性质，确定岩石破裂的模式，生成表达微地震源的矩张量矩阵；步骤2，建立所需勘探区域的地质速度场模型；步骤3，波动理论下，建立适用于描述微地震波场传播的弹性波波动方程；步骤4，在波动理论下，求解微地震弹性波波动方程，实现微地震的波场传播模拟；步骤5，模拟完成，输出微地震地面、井中多分量记录和纵横波的能量辐射模式。本发明的目的还可通过如下技术措施来实现：在步骤1中，通过对水力压裂过程中接收到的实际微地震数据的分析，获得微地震的量级，从而生成表达微地震源的矩张量矩阵M=M11M12M13M21M22M23M31M32M33]]>其中Mij为岩石破裂量级，矩张量中的每个元素代表一对方向相反的力的作用。在步骤2中，读取预先建立的所需勘探区域的地质速度场模型信息，建立所需勘探区域的地质速度场模型，即完成区域速度场建模。在步骤3中，建立的微地震弹性波波动方程为：ρ∂2ui(x,t)∂t2-cijkl∂2uk(x,t)∂xj∂xl=Mij∂[δ(x-xs)]∂xjS(t),]]>其中ui(x,t)和uk(x,t)为波场位移，cijkl为刚度系数，ρ为介质密度，x为空间点坐标，t为时间，三维情况下，i,j,k,l＝x,y,z，xs为震源点位置，S(t)为震源子波，M为矩张量。在步骤3中，利用步骤1获得的矩张量，代入微地震波动方程，使用等效体力法对方程右边的震源项进行等效离散。在步骤4中，利用交错网格高阶有限差分技术、伪谱法、有限元法、谱元法或迭代求解法求解微地震弹性波波动方程。本发明中的模拟微地震的弹性波正演方法，克服了射线理论高频假设的缺陷，避免Green函数法计算量大、模拟精度低的缺点，在充分考虑不同压裂模式所引起的微地震震源类型的前提下，使用等效体力法对微地震震源进行描述，通过波动理论进行地震波的传播模拟，能够快速的得到较射线理论更精确的模拟结果，且信息量更为丰富，并为后续的特征规律分析、定位方法研究以及震源参数反演提供更好的技术手段和工具。附图说明图1为本发明的模拟微地震的弹性波正演方法的具体实施例的流程图；图2为本发明的一具体实施例中理论记录(实线)、本发明模拟记录(点划线)和利用格林函数法模拟记录(虚线)三者振动曲线X分量比较的示意图；图3为本发明的一具体实施例中理论记录(实线)、本发明模拟记录(点划线)和利用格林函数法模拟记录(虚线)三者振动曲线Y分量比较的示意图；图4为本发明的一具体实施例中理论记录(实线)、本发明模拟记录(点划线)和利用格林函数法模拟记录(虚线)三者振动曲线Z分量比较的示意图。具体实施方式为使本发明的上述和其他目的、特征和优点能更明显易懂，下文特举出较佳实施例，并配合附图所示，作详细说明如下。如图1所示，图1为本发明的模拟微地震的弹性波正演方法的流程图。在步骤101，根据地质勘测的实际资料，分析岩石的性质，确定岩石破裂的模式。同时，通过对水力压裂过程中接收到的实际微地震数据的分析，获得微地震的量级，从而生成表达微地震源的矩张量矩阵其中Mij为岩石破裂量级。矩张量中的每个元素代表一对方向相反的力的作用。在步骤102，，读取预先建立的所需勘探区域的地质速度场模型信息如刚度系数cijkl，介质密度ρ；建立所需勘探区域的地质速度场模型，即完成区域速度场建模。在步骤103，波动理论下，建立适用于描述微地震波场传播的弹性波波动方程其中ui(x,t)和uk(x,t)为波场位移，cijkl为刚度系数，ρ为介质密度，x为空间点坐标，t为时间。三维情况下，i,j,k,l＝x,y,z，xs为震源点位置，S(t)为震源子波，M为矩张量。利用步骤101获得的矩张量，代入微地震波动方程使用等效体力法对方程右边的震源项进行等效离散。在步骤104，在波动理论下，利用交错网格高阶有限差分技术求解步骤103中的微地震波动方程，实现微地震的波场传播模拟；也可用伪谱法、有限元法、谱元法或迭代求解法实现。在步骤105，模拟完成，输出微地震地面、井中多分量记录和纵横波的能量辐射模式。图2-4为利用本发明的模拟实例。模拟中介质采用三维均匀介质，观测系统为地表接收，其震源矩张量见(1)式M=0M00M000000---(1)]]>其中M0为岩石破裂量级。图2-4展示了三个位移分量的一道振动曲线。其中实线为解析解，虚线和点划线分别是利用Green函数方法和本发明方法的模拟结果。可以看出，利用本发明方法得到的数值解与解析解基本一致，而Green函数方法由于存在一阶近似，误差偏大。且由于Green函数方法需要多次迭代，计算时间约为本发明方法的三倍。图2为微地震多分量记录的X分量，图3为Y分量，图4为Z分量。本发明引入天然地震中描述刻画震源的矩张量概念，实现对压裂震源的刻画。通过矩张量的定义，实现高效高精度的微地震波动方程数值模拟方法。本方法克服了射线理论高频假设的缺陷，避免了射线模拟下波现象缺失的问题；同时，本方法采用等价体力方式实现岩石破裂模式的震源实现，较常规动力学格林函数合成方法更加灵活快速。当前第1页1 2 3