一种扭振测试误差校正方法与流程

本申请旋转机械和信号处理
技术领域：
，更具体地说，涉及一种扭振测试误差校正方法。
背景技术：
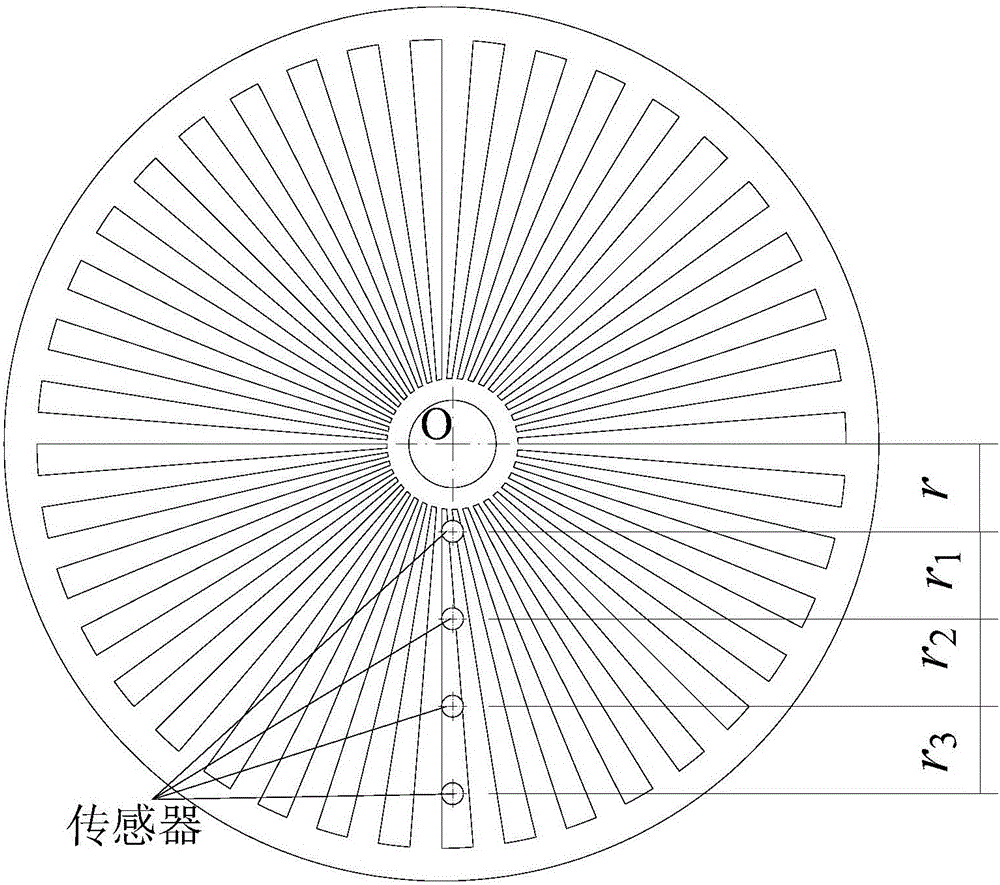
：扭振是反映系统是否存在谐振(共振)的危险程度的参数，主要与系统各组成部件的转动惯量和扭转刚度有关，即与设备的结构尺寸有关。扭振广泛存在于旋转机械上，由于扭振具有较强的隐蔽性且较大的危害性，因此对于扭振的准确测量就显得尤为重要。目前对于扭振的测量主要采用非接触式测量，即通过测量瞬时转速的波动(转速脉冲信号)来间接获取系统的扭振信号，瞬时转速作为扭振测试过程中的一个重要的中间量，它的测试精度直接影响着扭振的测试进度。然而在进行瞬时转速的获取的过程中需要人为地在旋转轴上安装码盘、齿盘和反光纸等部件，这些部件安装过程中的位置误差对瞬时转速的获取过程会产生很大的影响，从而会使得最终获得的扭振值出现较大的误差；其中，由于码盘的偏心情况而使得瞬时转速的获取产生误差，进而使得最终获得扭振值出现较大误差的情况较为常见。因此，亟需一种在码盘偏心情况下对扭振测试误差进行校正的方法。技术实现要素：为解决上述技术问题，本发明提供了一种扭振测试误差校正方法，以实现在码盘偏心情况下对扭振测试误差进行校正的目的。为实现上述技术目的，本发明实施例提供了如下技术方案：一种扭振测试误差校正方法，适用于校正由于码盘偏心产生的扭振测试误差，所述扭振测试误差校正方法包括：在位于码盘表面的预设线段上安装预设数量的传感器，所述预设线段为旋转轴的一条半径延长线；以距所述旋转轴中心距离由小到大的顺序对所述预设数量的传感器进行编号，记录除编号为1的传感器以外的各个所述传感器的位置参数；在所述旋转轴转速稳定时，采集每个所述传感器的转速脉冲信号；对采集的所述转速脉冲信号进行阶次分析，获得每个所述传感器采集的各阶扭振参数；将每个所述传感器采集的各阶扭振参数以及所述位置参数代入预设公式，获得校正后的各阶扭振值；所述预设数量为3或4，当所述预设数量为3时，所述预设公式为：其中，Bi0为所述校正后的第i阶扭振值，a为编号为2的传感器的位置参数；b为编号为3的传感器的位置参数；和为各个所述传感器采集的第i阶扭振参数；当所述预设数量为4时，所述预设公式为：其中，a为编号为2的传感器的位置参数；b为编号为3的传感器的位置参数；c为编号为4的传感器的位置参数；和为各个所述传感器采集的第i阶扭振参数。优选的，所述在位于码盘表面的预设线段上安装预设数量的传感器之前还包括：根据测量精度要求和测试条件要求确定所述预设数量。优选的，所述以距所述旋转轴中心距离由小到大的顺序对所述预设数量的传感器进行编号，记录除编号为1的传感器以外的各个所述传感器的位置参数包括：以距所述旋转轴中心距离由小到大的顺序对所述预设数量的传感器进行编号；记录编号为1的传感器距所述旋转轴中心的距离；记录相邻所述传感器之间的距离；根据编号为1的传感器距所述旋转轴中心的距离与相邻所述传感器之间的距离计算除编号为1的传感器以外的各个所述传感器的位置参数。优选的，当所述预设数量为3时，根据编号为1的传感器距所述旋转轴中心的距离与相邻所述传感器之间的距离计算除编号为1的传感器以外的各个所述传感器的位置参数的公式包括：a=rr+r1;]]>b=rr+r1+r2;]]>其中，r为所述编号为1的传感器距所述旋转轴中心的距离；r1为编号为2的传感器与编号为1的传感器之间的距离；r2为编号为3的传感器与编号为2的传感器之间的距离。优选的，当所述预设数量为4时，根据编号为1的传感器距所述旋转轴中心的距离与相邻所述传感器之间的距离计算除编号为1的传感器以外的各个所述传感器的位置参数的公式包括：a=rr+r1;]]>b=rr+r1+r2;]]>c=rr+r1+r2+r3;]]>其中，r为所述编号为1的传感器距所述旋转轴中心的距离；r1为编号为2的传感器与编号为1的传感器之间的距离；r2为编号为3的传感器与编号为2的传感器之间的距离；r3为编号为4的传感器与编号为3的传感器之间的距离。优选的，所述对采集的所述转速脉冲信号进行阶次分析，获得每个所述传感器采集的各阶扭振参数包括：利用瞬时转速提取滤波法提取所述转速脉冲信号的扭振阶次，获得每个所述传感器采集的各阶扭振参数。优选的，所述对采集的所述转速脉冲信号进行阶次分析，获得每个所述传感器采集的各阶扭振参数包括：利用瞬时转速提取滤波法提取所述转速脉冲信号的扭振阶次，获得每个所述传感器采集的各阶扭振的幅值和相位。从上述技术方案可以看出，本发明实施例提供了一种扭振测试误差校正方法，适用于校正由于码盘偏心产生的扭振测试误差，所述扭振测试误差校正方法通过首先将预设数量的传感器安装在码盘表面的预设线段上，并记录除编号为1的传感器以外的各个所述传感器的位置参数；然后采集每个所述传感器的转速脉冲信号，并对其进行阶次分析，获得每个所述传感器采集的各阶扭振参数；最后将每个所述传感器采集的各阶扭振参数以及所述位置参数代入预设公式进行计算，即可获得校正后的各阶扭振值，从而达到对由于码盘偏心而产生的扭振测试误差进行校正的目的。附图说明为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据提供的附图获得其他的附图。图1为本申请的一个实施例提供的一种扭振测试误差校正方法的流程示意图；图2为本申请的一个实施例提供的一种4个传感器在码盘表面的布置方式的示意图；图3为本申请的一个实施例提供的一种以旋转轴中心为原点建立的直角坐标系和极坐标系。具体实施方式下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。本申请实施例提供了一种扭振测试误差校正方法，适用于校正由于码盘偏心产生的扭振测试误差，如图1所示，所述扭振测试误差校正方法包括：S101：在位于码盘表面的预设线段上安装预设数量的传感器，所述预设线段为旋转轴的一条半径延长线；S102：以距所述旋转轴中心距离由小到大的顺序对所述预设数量的传感器进行编号，记录除编号为1的传感器以外的各个所述传感器的位置参数；S103：在所述旋转轴转速稳定时，采集每个所述传感器的转速脉冲信号；S104：对采集的所述转速脉冲信号进行阶次分析，获得每个所述传感器采集的各阶扭振参数；S105：将每个所述传感器采集的各阶扭振参数以及所述位置参数代入预设公式，获得校正后的各阶扭振值。其中，所述预设数量为3或4，当所述预设数量为3时，所述预设公式为：其中，Bi0为所述校正后的第i阶扭振值，a为编号为2的传感器的位置参数；b为编号为3的传感器的位置参数；和为各个所述传感器采集的第i阶扭振参数(具体的，为编号为1的传感器采集的第i阶扭振参数；为编号为2的传感器采集的第i阶扭振参数；为编号为3的传感器采集的第i阶扭振参数)；当所述预设数量为4时，所述预设公式为：其中，a为编号为2的传感器的位置参数；b为编号为3的传感器的位置参数；c为编号为4的传感器的位置参数；和为各个所述传感器采集的第i阶扭振参数具体的，为编号为1的传感器采集的第i阶扭振参数；为编号为2的传感器采集的第i阶扭振参数；为编号为3的传感器采集的第i阶扭振参数；为编号为4的传感器采集的第i阶扭振参数。在上述实施例的基础上，在本申请的一个实施例中，所述在位于码盘表面的预设线段上安装预设数量的传感器之前还包括：根据测量精度要求和测试条件要求确定所述预设数量。为了更好的理解本实施例提供的所述扭振测试误差校正方法，我们有必要对在使用码盘采集每个所述传感器的转速脉冲信号产生误差的原因进行研究。如图2所示，以预设数量为4为例，O点为所述旋转轴中心，4个所述传感器设置在所述旋转轴的一个半径延长线上；假设所述码盘的刻线无穷多，则当所述旋转轴转过任意一个角度时，所述码盘上都有相对应的刻度线经过所述传感器所在的S点。为了便于说明，以O点为原点，以OS方向为横轴建立一个如图3所示的Oxy直角坐标系。假设旋转轴实际的转角为α，所述传感器测量得到的测试转角为β，α和β均连续。偏心距OO1和OO2均为δ，编号为1的传感器距原点的距离OS为r，码线O2A2的长度为λ。同时，由于整个系统都在旋转，将各点在直角坐标系下的坐标映射到极坐标系下表示会带来很大方便。为了获取各点的极坐标，同样以O点为原点在附图3中建立一个极坐标系，则在极坐标下码盘中心O2的坐标可表示为δ·exp(jα)，图中O2C平行于OB1，可知直线O2A2的斜率为tan(α-β)，则该直线上任一点可表示为：sin(α-β)cos(α-β)=y-δsinαx-δcosα---(2)]]>将S点坐标(r，0)代入式(2)中得到：sin(α-β)cos(α-β)=-δsinαr-δcosα---(3)]]>整理式(3)，可得测试转角β与实际转角α的关系为：β=α+arctanδsinαr-δcosα---(4)]]>在偏心距δ较小的情况下，，则式(4)可用泰勒级数展开，为：β=α+Σn=0∞(-1)n12n+1(δsinαr-δcosα)2n+1---(5)]]>对式(5)进行一次微分，即可得到所述旋转轴的瞬时角速度信号，在进行零均值化处理，得到的角速度波动量即为在该偏心码盘上测得的扭振角速度信号。考虑到实际测量中安装半径r一般远大于偏心距δ，因此式(5)只分析n取1时泰勒级数的情况，将n＝1代入式(5)中并求到后可得所述旋转轴的角速度为：β·=α·+α·[δrcosα-δ2(r-δcosα)2-(δsinα)2(δrcosα-δ2)(r-δcosα)4]---(6)]]>将式(6)整理成以为变量的表达式将在零点处泰勒展开，省去式中项次数比较高的项，得到：β·=α·+α·(δrcosα+δ2r2cos2α+δ3r3cos3α)---(7)]]>由式(7)可知，在旋转轴本身不存在扭振的情况下，码盘偏心引起的误差主要影响扭振角速度的1、2、3阶量，且其幅值与旋转轴的角速度成正比。此外，第n阶误差的幅值与偏心比的n次方成正比。但在实际测量中，旋转轴本身的扭振必然存在，在稳态情况下，假设旋转轴存在k阶扭振角速度，则旋转轴的角速度可以表示为：式中，ω0表示旋转轴的平均角速度，Am表示各阶扭振角速度的幅值，表示各阶扭振角速度的相位。对式(8)进行积分得到旋转轴的转角为：则式(7)中的用贝塞尔函数分解有：cosα＝Re[exp(jω0t)·J](10)式中，表示参数为的第一类贝塞尔函数。相对于刚体转动，一般旋转轴本身存在的各阶扭振的角度幅值值比较小，接近于0，由贝塞尔函数的曲线可知式只有当n＝0时的值接近于1，其他情况几乎为0，因此式(10)进一步简化为：cosα＝Re[exp(jω0t)·J]≈cosω0t(11)同理有：cos2α≈cos2ω0t，cos3α≈cos3ω0t(12)将式(8)、(9)、(11)和(12)代入到式(7)中，得到：式(13)减去角速度的平均值即可得到了偏心状态下的码盘测得的扭振角速度为：由式(14)可得到第i阶扭振的误差△Ai的表达式为：到这里，我们就得到了利用处于偏心状态下的码盘测得的第i阶扭振的误差△Ai的表达式。下面针对式(15)我们进行误差校正的原理分析。由式(15)可知，实际测得的第i阶扭振的表达式为：其中，ω0表示旋转轴的平均角速度；Am表示各阶扭振角速度的幅值，m表示阶数；表示各阶扭振角速度的相位，m表示阶数；r表示标号为1的传感器距离旋转轴中心的距离；δ表示码盘的偏心距。由式(16)可知，测量得到的任一阶扭振结果的表达式中，项的次数都包含0、1、2、3次，观察表达式式(16)可以发现，当传感器相位不变而改变其安装半径，也就是偏心比发生变化时，式中第一项的幅值和相位均不变，第二项中的i次项会并入后三项中的某一项或者是大于等于的4次方的更高次幂项，但考虑到实际测量过程中偏心比一般较小，也就是说的4次项及更高此项很小，可忽略不计而对精度影响很小，合并后的包含的1-3次方的各项只是其系数发生变化，而各项的幅值和相位都没有改变，因此当在处于旋转轴同一半径延长线上而安装多个传感器同时测量时，各传感器测得的数据均由四部分组成，其中各个数据的第一项相同，而其余项各自对应成倍数关系；合理布置多个传感器，并同时进行测量，由于各误差部分在偏心比发生变化的情况下，相位不发生变化，只是幅值发生有规律的变化；因此，将各个传感器测量得到的结果合理进行计算就能达到消除误差的效果。在旋转轴同一半径延长线上安装h(h＝3或4)个相同的传感器，各个传感器距离旋转轴中心的距离依次为Rk(k＝1、2……h)。按照距离旋转轴中心由近到远将传感器依次编号，码盘的偏心距为δ，则各个传感器位置处的偏心比依次为安装好h个传感器后，采集旋转轴稳定旋转过程中的转速脉冲信号。对采集的所述转速脉冲信号进行阶次分析，获得每个所述传感器采集的各阶扭振参数。在上述实施例的基础上，在本申请的一个实施例中，所述对采集的所述转速脉冲信号进行阶次分析，获得每个所述传感器采集的各阶扭振参数包括：利用瞬时转速提取滤波法提取所述转速脉冲信号的扭振阶次，获得每个所述传感器采集的各阶扭振参数。具体的，所述传感器采集的各阶扭振参数包括所述传感器采集的各阶扭振的幅值和相位设编号为k的传感器的第i阶扭振参数为其中，k＝1、2……h。我们将以距所述旋转轴中心距离由小到大的顺序对所述预设数量的传感器进行编号，记录除编号为1的传感器以外的各个所述传感器的位置参数的具体方法限定如下：以距所述旋转轴中心距离由小到大的顺序对所述预设数量的传感器进行编号；记录编号为1的传感器距所述旋转轴中心的距离；记录相邻所述传感器之间的距离；根据编号为1的传感器距所述旋转轴中心的距离与相邻所述传感器之间的距离计算除编号为1的传感器以外的各个所述传感器的位置参数。当所述预设数量为3时，根据编号为1的传感器距所述旋转轴中心的距离与相邻所述传感器之间的距离计算除编号为1的传感器以外的各个所述传感器的位置参数的公式包括：a=rr+r1;]]>b=rr+r1+r2;]]>其中，r为所述编号为1的传感器距所述旋转轴中心的距离；r1为编号为2的传感器与编号为1的传感器之间的距离；r2为编号为3的传感器与编号为2的传感器之间的距离。当所述预设数量为4时，根据编号为1的传感器距所述旋转轴中心的距离与相邻所述传感器之间的距离计算除编号为1的传感器以外的各个所述传感器的位置参数的公式包括：a=rr+r1;]]>b=rr+r1+r2;]]>c=rr+r1+r2+r3;]]>其中，r为所述编号为1的传感器距所述旋转轴中心的距离；r1为编号为2的传感器与编号为1的传感器之间的距离；r2为编号为3的传感器与编号为2的传感器之间的距离；r3为编号为4的传感器与编号为3的传感器之间的距离。以布置四个传感器为例，编号为1的传感器与旋转轴中心的距离为r(r＝R1)，编号为3的传感器与编号为2的传感器之间的距离为r2；编号为4的传感器与编号为3的传感器之间的距离为r3，这样编号分别为2、3和4的传感器所在位置处的偏心比分别为其中各个传感器的第i阶扭振参数分别为依据式(16)按照项的次数对中各项进行编号，其中，的0次项记为Bi0，1次项记为Bi1，2次项记为Bi2，3次项记为Bi3，则有：则编号为2、3、4的三个传感器测得的所述各阶扭振参数的数值也可以用表示，将这四个方程合并为方程组由于之后的求解：易知式中即为旋转轴第i阶实际的扭振值，由方程组(18)可以解得：当布置三个传感器时，只能列出三个方程，也即不考虑上述分析中的3次项Bi3。三个传感器同样要布置在所述旋转轴的同一条半径延长线上，为了便于计算，去掉编号为4的传感器，同样用Bi0、Bi1、Bi2分别表示0、1、2次项，三个传感器测得的第i阶扭振值分别为依照方程组(18)的推导原理，构建布置三个传感器时的方程组为：求得当预设数量为3时的预设公式为：式(1A)和(1B)即为码盘处于偏心状态时，分别安装三个和四个传感器时利用所述扭振测试误差校正方法对扭振测试误差进行校正的预设公式，将所述位置参数(即a、b、c的值或a、b的值)以及用矢量形式表示的各个传感器测得的各阶扭振参数代入到式(1A)或式(1B)中即可得到校正后的各阶扭振值。通过上述分析可以发现，本申请实施例提供的所述扭振测试误差校正方法的校正公式较为简单，只需要代入所述位置参数以及用矢量形式表示的各个传感器测得的各阶扭振参数进行一次计算即可，计算过程相对简单。并且由于所述预设数量的传感器只需要布置在所述旋转轴的同一条半径延长线上即可，各个传感器之间的距离可以是任意的，只要能够知道各个传感器安装半径的比例关系即可，因此布置相对较容易，且操作也较为方便。在上述实施例的基础上，在本申请的一个具体实施例中，所述扭振测试误差校正方法包括：S201：根据测量精度要求和测试条件要求确定所述预设数量；S202：在位于码盘表面的预设线段上安装预设数量的传感器，所述预设线段为旋转轴的一条半径延长线；S203：以距所述旋转轴中心距离由小到大的顺序对所述预设数量的传感器进行编号；S204：记录编号为1的传感器距所述旋转轴中心的距离；S205：记录相邻所述传感器之间的距离；S206：根据编号为1的传感器距所述旋转轴中心的距离与相邻所述传感器之间的距离计算所述位置参数；S207：在所述旋转轴转速稳定时，采集每个所述传感器的转速脉冲信号；S208：利用瞬时转速提取滤波法提取所述转速脉冲信号的扭振阶次，获得每个所述传感器采集的各阶扭振参数；S209：将每个所述传感器采集的各阶扭振参数以及所述位置参数代入预设公式，获得校正后的各阶扭振值。为了便于验证本申请实施例提供的扭振测试误差校正方法的正确性，下面对所述扭振测试误差校正方法进行仿真计算。假设旋转轴的角速度为：ω=ω0+30cos(ω0t+π4)+20cos(2ω0t+π3)+18cos(3ω0t+π6)+12cos(4ω0t+3π4)+8cos(5ω0t+15π12)+5cos(6ω0t+5π6)---(19)]]>单位为°/s，其中n0为旋转轴转速，单位为r/min。仿真转速设置为两组，第一组转速为800r/min，第二组转速为1500r/min。根据测量精度的需要和实验允许的条件，确定所述预设数量，在本实施例中，所述预设数量确定为4。安装传感器，采集稳定转速下扭振脉冲信号：如附图1所示，在旋转轴同一半径延长线上安装四个相同的传感器，为便于计算，将1、2、3、4号传感器处的偏心比分别设置为和此时，a＝1/2、、b＝1/3c＝1/4，布置好传感器之后，采集旋转轴稳速旋转过程中的每个所述传感器的转速脉冲信号。码盘偏心情况下，由理论推导可得传感器测试转角与实际转角的关系为：β=α+arctanδsinαr-δcosα---(4)]]>将(19)式经过积分换算成角度信号后代入式(4)中，进行数值微分后得到测量的角速度，去除平均角速度即可得到各个传感器测得的旋转轴各阶扭振角速度的幅值和相位，通过实验验证发现，由此得到的传感器采集的各阶扭振参数与码盘偏心时传感器实际采集的各阶扭振参数有很高的一致性，因此上述计算结果可以代表传感器实际采集的各阶扭振参数。将旋转轴转速为800r/min和1500r/min时计算得到的数据分别汇集到表1和表2中。表1旋转轴转速为800r/min时四个传感器测得的各阶扭振幅值和相位表2旋转轴转速为1500r/min四个传感器测得的各阶扭振幅值和相位对采集的所述转速脉冲信号进行阶次分析，获得每个所述传感器采集的各阶扭振参数具体如下：对于旋转轴转速为800r/min，由表1知四个传感器测得的旋转轴扭振的一阶量分别为将这四个向量以及a、b、c的值代入公式(1B)中进行计算，得到B10＝29.997ej43.65π/180。也即校正后得到的旋转轴的实际一阶扭振值幅值为29.997°/s，相位43.65°。用同样的方法求得各阶次校正后的幅值和相位汇集到表3中。表3旋转轴转速为800r/min轴扭振实际量与校正量对比由表3可看出，将四个传感器测得的数据代入到校正公式(1B)进行计算后，得到的校正后轴的各阶扭振量与轴理论扭振量几乎相同，幅值的相对误差均在0.1％以下，由于相位可以为零，因此其相对误差没有意义，其绝对误差最大为5.3，符合工程运用的要求。同理，对于旋转轴转速为1500r/min时，用同样的方法求得各阶次校正后的幅值和相位汇集到表4中。表41500r/min轴扭振实际量与校正量对比由表4可看出，将四个传感器测得的数据代入到校正公式(1B)进行计算后，得到的校正后轴的各阶扭振量与轴实际扭振量几乎相同，幅值的相对误差均在0.15％以下，相位绝对误差最大为9.94，符合工程运用的要求。理论上布置传感器越多，校正精度越高，因此在本申请实施例中，所述预设数量优选为4。综上所述，本申请实施例提供了一种扭振测试误差校正方法，适用于校正由于码盘偏心产生的扭振测试误差，所述扭振测试误差校正方法通过首先将预设数量的传感器安装在码盘表面的预设线段上，并记录除编号为1的传感器以外的各个所述传感器的位置参数；然后采集每个所述传感器的转速脉冲信号，并对其进行阶次分析，获得每个所述传感器采集的各阶扭振参数；最后将每个所述传感器采集的各阶扭振参数以及所述位置参数代入预设公式进行计算，即可获得校正后的各阶扭振值，从而达到对由于码盘偏心而产生的扭振测试误差进行校正的目的。并且本申请实施例提供的所述扭振测试误差校正方法的校正公式较为简单，只需要代入所述位置参数以及用矢量形式表示的各个传感器测得的各阶扭振参数进行一次计算即可，计算过程相对简单。进一步的，由于所述预设数量的传感器只需要布置在所述旋转轴的同一条半径延长线上即可，各个传感器之间的距离可以是任意的，只要能够知道各个传感器安装半径的比例关系即可，因此布置相对较容易，且操作也较为方便。本说明书中各个实施例采用递进的方式描述，每个实施例重点说明的都是与其他实施例的不同之处，各个实施例之间相同相似部分互相参见即可。对所公开的实施例的上述说明，使本领域专业技术人员能够实现或使用本发明。对这些实施例的多种修改对本领域的专业技术人员来说将是显而易见的，本文中所定义的一般原理可以在不脱离本发明的精神或范围的情况下，在其它实施例中实现。因此，本发明将不会被限制于本文所示的这些实施例，而是要符合与本文所公开的原理和新颖特点相一致的最宽的范围。当前第1页1 2 3