一种利用测量信息优化分布式EKF估计过程的SLAM方法与流程

在利用测量信息优化分布式EKF估计过程的SLAM方法中，分布式结构将时变的观测信息分布化处理，根据路标点信息对应建立若干平行的子系统，并且子系统维数不随时间变化。各子系统单独进行滤波估计，将各自的估计结果送到主滤波器中，主滤波器在保证系统在精度较高或一致性较高的情况下合理地做出融合判定，最后输出最优的机器人位姿估算结果。属于机器人自主导航领域。
背景技术：
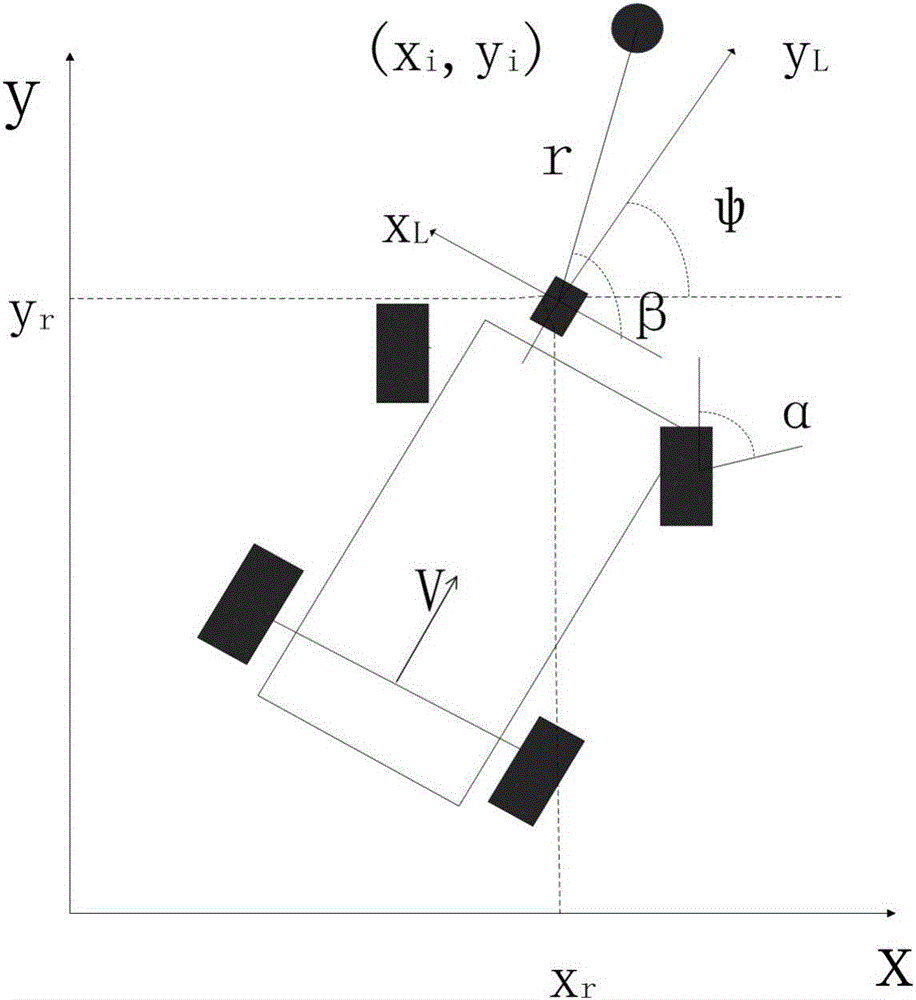
：SLAM(SimultaneousLocalizationandMapping)即同步定位与地图构建，其基本思想是：让机器人在未知环境中从未知位置开始移动,通过自身所带传感器扫描到的路标点的信息进行自身位置估计，同时构建增量式地图。在SLAM过程中，根据观测信息进行实时的地图估计与更新，其中滤波器设计，数据融合算法都是关键问题。SLAM问题可以建立在不同的算法结构中，对于传统的集中式SLAM，将机器人位姿和路标点信息均加入到状态向量中，在整个SLAM滤波过程中，无论采用哪种滤波方式，状态向量由于一直附带时变的路标点信息进行后续滤波运算，随着路标点数量的增多状态向量维数也不断增多，计算量相应增大，并且根据路标点的观测情况动态时变。本发明中SLAM算法采用分布式结构，在分布式结构中将机器人位姿及路标点信息进行分布化处理，每个有效的路标点对应一个子滤波器。因此，状态向量的维数相对固定，不会随着时变的路标点信息而变化，每一个子滤波器都有各自的状态方程和观测方程，各子滤波器的估计结果都被传送到主滤波器进行融合运算。在主滤波器中，根据各个子滤波器的估计结果及相应的误差情况计算机器人位姿的最终结果。由于扩展卡尔曼滤波方法的简单性与有效性，在各子滤波器中通常选用EKF算法。但是，EKF线性化过程忽略高阶项产生的线性误差导致了子滤波器估计精度存在局限性。主滤波器的核心是融合算法，选择单一的引入误差协方差矩阵或新息矩阵信息参与数据融合过于单薄，难以保证系统精度。技术实现要素：本发明针对分布式SLAM系统中EKF子滤波器估计精度存在的局限性问题，采用由传感器直接测得的观测量计算滤波器雅克比矩阵，提高了子滤波器估计精度。并且考虑到一致性对系统的影响，改进分布式系统融合的方案，提出利用误差协方差阵和匹配信息共同参与数据融合过程的方式对算法进行优化。下文将具体描述优化分布式结构中的子滤波器以及分布式系统的融合方案的过程。最后通过真实实验证明了本发明算法的可行性与有效性。机器人的运动模型和观测模型如图1所示。在分布式SLAM问题中，假设机器人的姿态表示为其中(xr,yr)表示机器人在地图中的坐标，表示航向角。路标点在地图中的位置表示为：mi＝(xi,yi)T,i＝1:n，其中mi表示第i个路标点对应的位置信息，(xi,yi)表示路标点在地图中的坐标。t时刻机器人的状态矢量表示为Xt＝(xt,rT,mt,iT)T。机器人的运动学模型可用公式(1)描述st＝f(st-1,ut)+wt(1)其中，移动机器人运动模型描述了t时刻机器人的状态在运动的控制信号ut和噪声干扰wt作用下随时间的变化过程。wt表示过程噪声，用来表示机器人运动过程中存在的不确定性误差。机器人的观测模型可以用公式(2)表示Ζ(t)＝h(xr(t),mi(t))+v(t)(2)其中Z为t时刻机器人通过激光测距仪所获得的观测信息(r,β)T，r表示机器人与路标点间的距离，β表示第i个路标点相对机器人的方向角，v为测量误差。假设t时刻观测到n个有效的特征点，分布式系统可表示为：X·r=f(Xr)+wz1=h(Xr(t),m1)+v1X·r=f(Xr)+wz2=h(Xr(t),m2)+v2...X·r=f(Xr)+wzn=h(Xr(t),mn)+vn---(3)]]>可见，在分布式SLAM中，根据观测到的路标点信息建立相互平行的子滤波器，每一个子滤波器都有各自的状态方程和观测方程。最终每一个子滤波器的估计结果都被传送到主滤波器，而在主滤波器中，根据各个子滤波器的估计结果及相应的误差情况计算出机器人位姿的最优结果。分布式滤波器结构图如图2。在分布式SLAM算法子滤波器估计单元中，EKF算法的第一步是根据运动模型和t-1时刻的状态对t时刻状态进行预测x‾t,r*x‾t,i*=f(x‾t-1,r,ut-1)x‾t-1,i---(4)]]>其中，和是机器人在t-1时刻所估计的机器人位置结果和路标点位置结果。第i个子系统t时刻的观测方程具体形式如下：解决SLAM问题时，EKF是在噪声符合零均值的高斯白噪声的假设下，利用将f(xt-1,rut-1)和h(xr(t),mi(t))展成泰勒级数并略去二阶以上高阶项从而得到非线性系统的线性化模型。因此，EKF关键的步骤是准确地求解状态方程和观测方程的两个雅克比矩阵。计算状态转移雅克比矩阵▿ft-1=∂f∂Xr|x‾t-1,r---(6)]]>计算观测信息雅克比矩阵▿ht=∂h∂X|x‾t*---(7)]]>预测结果的协方差阵如下：Pt*=Prr,t*Pri,t*Pir,t*Pii,t*=▿ft-1Prr,t-1▿ft-1T+Qt-1▿ft-1Pri,t-1Pir,t-1▿ft-1TPii,t-1---(8)]]>Pir,t-1=Pri,t-1T]]>其中Prr,t-1和Pri,t-1分别是t-1时刻机器人状态向量协方差和机器人与路标点状态向量的协方差。Pii,t-1和Qt-1分别是t-1时刻路标点状态向量的协方差和机器人运动的过程噪声的协方差。t时刻第i个子系统根据运动模型预测的和Pt*按照以下方式进行更新过程：Ki(t)=Pi*(t)▿hiT[▿hiPi*(t)▿hiT+Ri]-1,i=1,2...,n---(9)]]>X‾i(t)=X‾i*(t)+Ki(t)[Zi(t)-Hi(t)X‾i*(t)],i=1,2...,n---(10)]]>Pi(t)=[I-Ki(t)▿hi]Pi*(t),i=1,2...,n---(11)]]>其中，Ki(t)和分别是子滤波器t时刻的卡尔曼增益和观测方程的雅克比矩阵，Rt代表观测噪声矩阵，和Pi(t)分别代表子滤波器t时刻对应的状态向量估计值和相应的协方差。可见，t时刻子系统的位姿估计是根据泰勒一阶展开通过线性化的h(Xt)进而计算得到的，即Z=h(Xt)≈h(X0)+▿h(Xt-X0)---(12)]]>其中X0表示观测方程线性化时进行泰勒展开时所在的点，即根据运动模型所预测的点最后，将Z＝Zt代入时，得到EKFSLAM的最优估计结果。当观测方程在进行泰勒展开时的斜率是如下形式时，拥有最高的估计精度，kreal=Zt-h(X0)Xt-X0---(13)]]>当将kreal和Zt分别代入Ht和Z中，则Xt能被最精确地估计。如图3所示。在图3中，X0处的三条曲线A,B,C分别代表采用不同计算方法求出的X0处切线，即中所对应的各项值。其中，曲线A对应的是式(12)中的算法，即理论上最接近要求的计算值kreal，曲线C对应的是传统EKF中的计算值，而曲线B则表示通过利用各种优化的方法，试图将中对应的k在kEKF的基础上靠近真实观测方程雅克比矩阵中各项的kreal。基于此种思想，可以结合系统的观测方式和预测方式，设计适合实际系统的求取方法，从而得到精度更优的滤波器性能。针对以上非线性系统的线性化误差分析，改进的关键点是采用何处的X值进行线性化。结合分布式独有的结构，即对于各子滤波器观测到的路标点情况，分别计算相应的线性化结果，最终融合得到最优的估计结果。每一个子滤波器对应不同的线性化结果hi，由于各子滤波器的雅克比矩阵hi存在差异性，根据线性化尽可能最优的原则，采用均值逼近的方法，对进行改进。根据分布式EKF中子滤波器t时刻迭代更新的计算式(14)Kt=Pt-▿htT(▿htPt-▿htT+Rt)-1---(14)]]>其中观测方程的雅克比矩阵可以表示为式(15)的形式▿ht=-xi-xr(xi-xr)2+(yi-yr)2-yi-yr(xi-xr)2+(yi-yr)20yi-yr(xi-xr)2+(yi-yr)2yi-yr(xi-xr)2+(yi-yr)2-1001---(15)]]>如式(15)，在整个扩展卡尔曼滤波过程中，传统算法中将里程计数据、激光传感器数据代入滤波器过程得出状态估计结果，再代入式(15)中。由于得到的机器人位姿、路标点位置并不准确，该处理方式易造成的不准确，故提出如下的算法：式(15)中的表达式可以借助观测量，通过如下式(16)的表示方法进行求取：xt-xt,i=-rt*sign(cos(βt+φt-π2))1+tan2(βt+φt-π2)yt-yt,i=-rt*sign(cos(βt+φt-π2))*|tan(βt+φt-π2)|1+tan2(βt+φt-π2)---(16)]]>虽然t时刻理想状况的xreal无法直接得到，但可以由观测量间接推导得到，分别将由激光传感器得到的rt、βt和估计的航向角φt代入式(17)中进行计算，进而得到在点xreal下求得的相应观测方程雅克比矩阵则式(14)中的可以表示为如下形式：▿hnew=(▿hx*+▿hxreal)/2---(17)]]>改进后的t时刻第i个子系统的估计过程如下：Ki(t)=Pi*(t)▿hi,newT[▿hi,newPi*(t)▿hi,newT+Ri]-1,i=1,2...,n---(18)]]>X‾i(t)=X‾i*(t)+Ki(t)[Zi(t)-Hi(t)X‾i*(t)],i=1,2...,n---(19)]]>Pi(t)=[I-Ki(t)▿hi,new]Pi*(t),i=1,2...,n---(20)]]>考虑到一致性对系统的影响，本发明改进了分布式系统融合的方案，通过协方差矩阵子模块和匹配信息子模块，充分发挥分布式结构下观测信息的作用，保证系统在精度较高或一致性较高的情况下均能合理地做出融合判定。首先，利用误差协方差阵定义融合权重：设第i个子滤波器协方差阵为Pi，定义相应子滤波器在融合过程中的权重为δp,i。δp,i=1/PiΣi=1N(1/Pi)---(21)]]>依据以上定义，协方差阵Pi表征子滤波器的精度情况，子滤波器对应的协方差越大，说明该子滤波器的估计精度相对较低。相反，协方差阵越小，表征子滤波器的估计精度较高，应当令主滤波器更多继承该子滤波器的估计值，即该子滤波器权重值较大。协方差矩阵Pi描述子滤波器估计的精度情况，其主要描述当前时刻t的子滤波器权重情况，但从时间的维度上，无法反映从时刻t-1到t的子滤波器准确情况，为了衡量在运行过程中t-1到t时刻子滤波器的精度情况，并且使其反映到子滤波器的权重上,考虑在数据融合中引入匹配误差，从而丰富信息融合过程。同时需要考虑的是，由于子滤波器在运行过程中，其对某一路标点的“置信度”会随着系统运行的时间逐渐增高，这一规律是影响分布式系统一致性的重要原因，当观测噪声R无穷大时，看作近似对系统一致性没有影响，而如此则会降低子滤波器精度。所以，当子系统运行时，既需要精度高时实现合理性的融合，又需要在噪声较大而一致性较好时实现合理性的融合。从让系统最大限度地挖掘观测信息中所表征的特性，以及考虑一致性影响的角度出发，加入能够反映子滤波器测量噪声情况的匹配误差信息参与融合算法。该方法中的融合系数是以相邻时刻的临域匹配值大小来确定的，在机器人运行过程中，每一时刻的观测量都要进行匹配过程，在该过程中，是以匹配成功的路标点t-1和t时刻在地图上的映射值来衡量子滤波器性质。设t时刻的观测到的第i个路标点的坐标为(xi,t,yi,t)，地图中与之匹配的t-1时刻的路标点的坐标为(mix,t-1,miy,t-1)。定义匹配误差为同一路标点相邻时刻的距离误差，表示为ri。则有ri=(xi,t-mix,t-1)2+(yi,t-miy,t-1)2---(22)]]>此时，利用匹配误差定义融合权重：设第i个子滤波器匹配误差为ri，定义相应子滤波器在融合过程中的权重为δr,i。δr,i=1/riΣi=1N1/ri---(23)]]>根据以上定义，匹配误差用来衡量各子滤波器的可信赖程度。子滤波器的匹配误差越大，该子滤波器的观测噪声越大，子滤波器的观测精度越低，融合时子滤波器的信任度低，该自滤波器的权重值就越小；相反，子滤波器的匹配误差越小，该子滤波器的观测噪声越小，子滤波器的观测精度越高，融合时给与该子滤波器较高的信任度，即该子滤波器的权重值就越高。在本文的融合算法中，每个子系统存在以上两个融合子模块，即误差协方差模块和匹配融合模块。两个子模块分别采用协方差阵各项系数以及匹配最小邻域的误差进行权重的求解，最后，按照式(24)可以通过子模块的权重，计算最终的权重分配情况：δp,i·α+δr,i·γ＝ηi(24)在公式(24)中δp,i是第i个子系统由协方差子模块计算出的权重值，δM,i是第i个子系统由匹配融合模块计算出的权重值。ηi是改进的信息融合方法综合计算出的子系统权重。而α和γ分别是δp,i和δM,i在改进的信息融合方法中所占的比例，其中α和γ服从公式(25)。α+γ＝1(25)因此，主滤波器输出的t时刻机器人位姿的最优估计结果满足公式(26)。X‾r(t)=η1X‾r,1(t)+η2X‾r,2(t)+...ηnX‾r,n(t)---(26)]]>附图说明图1：机器人的运动模型和观测模型图2：分布式滤波器结构图图3：EKF线性化误差示意图图4：优化的分布式SLAM原理框图图5：移动平台示意图图6：椭圆形实验环境示意图图7：IDH-EKF算法和DH-EKF算法路径估计结果图8：IDH-EKF算法和DH-EKF算法与GPS数据的误差比较(X轴方向)图9：IDH-EKF算法和DH-EKF算法与GPS数据的误差比较(Y轴方向)图10：矩形实验环境示意图图11：IDH-EKF算法和DH-EKF算法路径估计结果具体实施方式步骤1：建立模型机器人模型及坐标系如图1所示，以机器人初始时刻的位置为坐标原点，以正东和正北方向为x轴和y轴的正方向。将整个状态向量分为机器人位姿估计和路标估计共五维状态，t时刻机器人状态矢量表示为Xt＝(xt,rT,mt,iT)T。设机器人的姿态表示为其中(xr,yr)表示机器人在地图中的坐标，表示航向角。路标点在地图中的位置表示为mi＝(xi,yi)T,i＝1:n，其中mi表示第i个路标点对应的位置信息，(xi,yi)表示路标点在地图中的坐标值。步骤2：初始化地图初始化，利用激光传感器扫描数据计算得到的路标点位置信息建立环境地图。步骤3：地图匹配并建立分布式子滤波器。获取机器人t时刻测得的路标点信息，并与已在全局地图中存储的路标点信息相匹配。对于t时刻匹配失败的路标点信息，直接将其添加至全局地图；对于t时刻成功匹配的路标点，利用公式(3)分别对应建立子滤波器。步骤4：子滤波器线性化利用公式(6)、(7)计算得到状态方程和观测方程的雅克比矩阵。根据公式(15)、(16)、(17)给出的新的线性化方法，可以得到子滤波器雅克比矩阵新的计算方法。改进后子滤波器的估计更新过程如公式(18)、(19)、(20)所示。步骤5：子滤波器滤波过程通过扩展卡尔曼滤波算法对上述步骤中建立的各个子滤波器的状态向量和协方差分别进行预测和更新。预测阶段：利用t-1时刻机器人位姿估计和该子滤波器对应的协方差矩阵，预测t时刻状态和协方差的先验估计值，如公式(4)、(8)所示。更新阶段：有了t时刻状态的预测结果，然后再收集现在状态的测量值。结合预测值和测量值，可以通过式子(9)，(10)和(11)得到现在状态的最优化估算值和协方差的更新值。步骤6：计算融合权值根据步骤5中各个子滤波器得到的机器人状态的最优估算值以及误差协方差矩阵，利用公式(21)计算每个子滤波器协方差矩阵的权重；根据公式(22)得到子滤波器的匹配误差值，利用公式(23)计算每个子滤波器匹配模块的权重。步骤7：建立主滤波器，并对各子滤波器的结果进行数据融合由公式(24)、(25)得到主滤波器中各子滤波器的融合权重。把各子滤波器中机器人位姿的状态向量及其权值传送给主滤波器，利用公式(26)主滤波器对各子滤波器中的数据进行融合计算，最终得到机器人位姿的最优估计，输出结果。本文利用测量信息优化分布式EKF估计过程的SLAM方法的原理框图如图4所示。下面通过真实实验对本发明提出的利用测量信息优化分布式EKF估计的SLAM方法进行验证。实验所用平台是自己搭建的两轮小车，传感器使用URG-04LX的激光传感器，移动平台的实物图如图5。实验所用的环境是椭圆形和长方形跑道，以长筒作为路标点在跑道两旁随机摆放，椭圆形实验环境如图6所示，矩形实验环境如图10所示，圆点表示小车起始位置，箭头指示方向为小车行驶方向，具体路径如图所示。通过使用本发明算法和传统的分布式SLAM算法对比，证明本算法的可行性和有效性。椭圆形跑道实验结果对比如图7，虚线(DH-EKF)表示的是单纯利用航向辅助分布式EKF估计的运动轨迹，图中实线(IDH-EKF)是基于本文利用测量信息优化分布式EKF估计过程的SLAM方法得到的，两者均能在运行一周后停留在起始点附近，图中标注的三个椭圆形区域为GPS的测算区域。利用场地环境的GPS测定结果中搜星数目较为理想的三段GPS数据为基准，三段GPS时间起始点分别是：93.53s，138.42s，318.43s，每个时间段所对应的两种算法在x轴方向和y轴方向上与GPS数据的误差情况如图8和图9所示。矩形跑道实验结果对比如图11，虚线(DH-EKF)表示的是利用基于航向辅助分布式SLAM的运动轨迹，可以观察出其运行轨迹大致符合矩形轨道，但最终并没有能够回到初始起点；图中实线(IDH-EKF)是基于本文利用测量信息优化分布式EKF估计过程的SLAM方法得到的，其估计轨迹符合矩形轨道规律，同时，轨迹终点接近原点，可见其收敛性更好。通过上述两组实验证实，本发明中的优化方法能有效地提高分布式SLAM算法在特殊环境变化时的稳定性和精度。当前第1页1 2 3