一种面向机械故障诊断的振动信号重构方法与流程

本发明属于振动信号处理技术领域，主要涉及机械设备振动信号的处理技术。

背景技术：

机械设备运行状态信息的获取是系统故障诊断的前提。由于振动信号自身实时性、周期性以及加速度传感器体积小，频带宽，易安装，高频响应稳定等特性，振动信号已经成为当前机械系统故障诊断中应用最广泛的信息载体。针对旋转机械关键零部件，基于振动信号频谱检测实现故障诊断的方法应用极为广泛。诊断过程中，振动信号滤波去噪(预处理)是关键，也是信号处理领域的研究热点和难点，其有效性直接决定了方法的可行性。常用的去噪方法通常基于小波变换，经验模态分解，谱峭度，盲源分离，自回归模型等算法，均取得不错的效果，但也存在过度依赖于经验知识和人工确定参数等局限性。

近年来，自压缩采样理论被论证，根据数据的可压缩性，通过低维欠奈奎斯特数据实现高维采样，极大地推动了字典学习在数据分类，信息压缩，图像处理等领域的发展。为了提高故障诊断的有效性，本发明更注重机械系统结构和信号本质，区别于传统去噪方法单纯减弱或消除振动信号噪声成分，采用基于非负K奇异值分解(NN-K-SVD)算法改进的字典学习算法重构振动信号，得到一种面向机械故障诊断的振动信号重构方法。

技术实现要素：

本发明的目的是提供一种面向机械故障诊断的振动信号重构方法，它能有效地重构振动信号并解决机械系统故障诊断问题。

本发明的目的是通过以下技术方案来实现的：一种面向机械故障诊断的振动信号重构方法，在非负条件下，对振动信号进行更为稀疏的编码，提高振动信号频谱检测的有效性。首先，由加速度传感器采集机械系统一维原始振动信号，重叠、分割得到列向量，并构成训练样本M。初始化学习字典D，基于非负基追踪(NN-BP)算法和非负K奇异值分解(NN-K-SVD)算法对学习字典D进行改进，通过更新稀疏编码矩阵C和学习字典D，交替迭代生成最终学习字典和对应的最终稀疏编码矩阵计算得到更新样本逆叠加重构信号。原始振动信号通过改进的字典学习算法更逼近信号本质结构，达到了较优的预处理效果，有利于通过提取重构信号的包络谱实现故障诊断。

具体实现步骤包括：

第一步，对机械系统连续的一维原始振动信号进行采样，将原始振动信号重叠、分割得到列向量，构成训练样本M：

M＝M₀+δ

式中，M₀表征理论上无噪声成分，δ表征噪声成分；

第二步，初始化学习字典D＝[d₁,d₂,...]，每一列对应一原子d，基于非负基追踪算法对训练样本M进行稀疏编码，得到初始化稀疏编码矩阵C：

${\min }_C\left|\right|M-DC|{|}_2^2+2\mathrm{\ω}\ΣC$

式中，学习字典D、训练样本M、稀疏编码矩阵C的任意元素均大于0，对于任意原子d，||d||＝1，常数ω＞0，表征振动信号重构精度和稀疏性的相对数值关系；第一项求M-DC的l²范数重构误差，第二项是稀疏编码惩罚项，约束稀疏分布，确保能量函数逐步减小。

第三步，固定稀疏编码矩阵C，基于非负K奇异值分解算法优化更新学习字典D：

D^t＝D^t-1-υ(D^t-1C^t-1-M)(C^t-1)'

式中，t是迭代次数，(.)'是矩阵转置，迭代步长υ＞0，原子d＜0时归零，确保学习字典D非负。

第四步，固定学习字典D，基于非负基追踪算法进行稀疏编码，更新对应的稀疏编码矩阵C：

C^t＝C^t-1.×(D^t'M)./(D^t'D^tC^t-1+ω)

式中，.×和./是矩阵对应位置元素相乘除，稀疏编码矩阵C非负，确保达到要求精度下全局最小值。

第五步，循环第三步和第四步，交替迭代更新得到最终学习字典和最终稀疏编码矩阵

第六步，计算更新样本逆叠加重构信号：

$\hat{M}=\hat{D}\hat{C}$

式中，求得的更新样本相较于训练样本M少了部分噪声成分。

第七步，逆叠加重构信号，提取重构信号的包络谱实现故障诊断。

本发明与现有技术相比的优点和效果：

(1)本发明主要思想是通过原始振动信号自身驱动构成训练样本进行信号预处理，区别于传统去噪方法单纯减弱或消除振动信号噪声成分，重构信号更符合振动信号本质和内在规律。

(2)本发明对原始振动信号在学习字典域进行稀疏表示，降低了数据在存储和传输的成本。

(3)本发明采用改进的字典学习算法重构振动信号，对K-SVD算法和NN-K-SVD算法进行改进，添加了非负约束，实现信号局部特征提取，得到的编码更稀疏，有益于数据压缩，优化和简化了算法。

附图说明

图1为本发明的面向机械系统故障诊断的振动信号重构方法框图

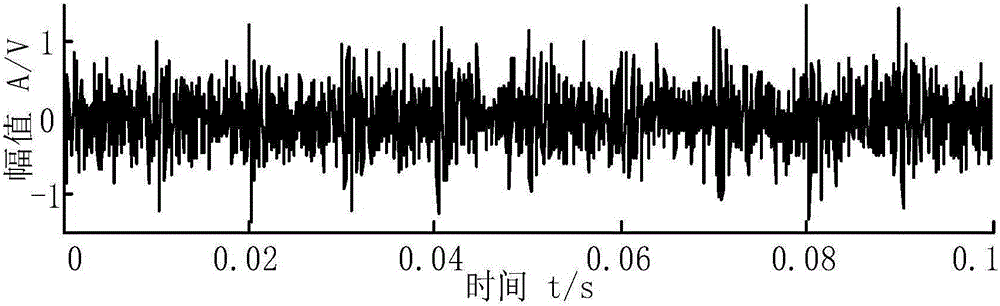
图2为本发明实施例原始振动信号

图3为本发明实施例不含噪声的振动信号

图4为本发明实施例改进的字典学习算法重构振动信号

具体实施方式

下面结合附图，对本发明作进一步的描述，方法框图如图1所示。

(1)仿真采集得到机械系统振动信号如图2，其中包含的无噪成分如图3，随机截取2048个数据点，将原始信号重叠72个数据点分割得到含有80个数据点的列向量，构成训练样本M。

M＝M₀+δ

式中，M₀表征理论上无噪声成分，δ表征噪声成分。

(2)初始化学习字典D＝[d₁,d₂,...]，每一列对应一原子d，尺寸80×10。基于非负基追踪算法对训练样本M进行稀疏编码，得到尺寸10×247的初始化稀疏编码矩阵C：

${\min }_C\left|\right|M-DC|{|}_2^2+2\mathrm{\ω}\ΣC$

式中，学习字典D、训练样本M、稀疏编码矩阵C的任意元素均大于0，对于任意原子d，||d||＝1，常数ω＞0，表征振动信号重构精度和稀疏性的相对数值关系。第一项求M-DC的l²范数重构误差，第二项是稀疏编码惩罚项，约束稀疏分布，确保能量函数逐步减小。

(3)固定稀疏编码矩阵C，基于非负K奇异值分解算法优化更新学习字典D：

D^t＝D^t-1-υ(D^t-1C^t-1-M)(C^t-1)'

式中，t是迭代次数，(.)'是矩阵转置，迭代步长υ＞0，原子d＜0时归零，确保学习字典D非负。

(4)固定学习字典D，取稀疏阀值3，基于非负基追踪算法进行稀疏编码，更新对应的稀疏编码矩阵C：

C^t＝C^t-1.×(D^t'M)./(D^t'D^tC^t-1+ω)

式中，.×和./是矩阵对应位置元素相乘除，稀疏编码矩阵C非负，确保达到要求精度下全局最小值。

(5)循环(3)和(4)，交替迭代20次，得到最终学习字典和最终稀疏编码矩阵

(6)计算更新样本逆叠加得到重构信号如图4。

$\hat{M}=\hat{D}\hat{C}$

式中，求得的更新样本相较于训练样本M少了部分噪声成分。

(7)逆叠加重构信号，提取重构信号的包络谱实现故障诊断。

本实施例中核心算法由C语言编写完成，人机交互界面和逻辑操作程序由Python语言编写完成。结果可知，原始振动信号经本发明提供的方法得到的重构信号，有效地保留了原始振动信号本质和内在规律成分，获得预处理的有益效果，达到压缩采样目的，提高振动信号频谱检测的有效性，实现机械系统故障诊断。