一种消除脉冲星到达时间数据中宽频时域干扰的方法与流程

本发明涉及天体物理技术领域，更具体地说，涉及一种消除脉冲星到达时间数据中宽频时域干扰的方法。

背景技术：

脉冲星是20世纪60年代四大天文发现之一，它的发现对当代天体物理的发展产生巨大的影响，相关研究工作曾分别两次获得诺贝尔物理学奖，这表明脉冲星的观测和理论研究具有重大的科学意义，脉冲星的观测研究一直是天体物理领域的热点，它是研究极端物理条件下物质性质和物理规律的“天然实验室”。

脉冲星最显著的一个特点就是具有极其稳定的自转周期，长期监测结果表明，其周期的长期稳定性可以和原子钟相媲美，甚至优于原子钟。射电天文观测是利用射电望远镜接收来自宇宙空间的脉冲星的脉冲信号，对脉冲星的数据进行周期折叠获得脉冲星的辐射轮廓及脉冲星的信号到达地球的时间，即脉冲星到达时间。脉冲星的研究主要集中在脉冲星的辐射轮廓及到达时间研究，脉冲星轮廓研究，可以研究脉冲星本身的辐射特性及辐射过程；脉冲星到达时间研究可以研究脉冲星的稳定性及脉冲星的应用研究，如脉冲星计时及脉冲星导航研究。

由于脉冲星信号包含大量的系统噪声和射电干扰噪声，对脉冲星的研究，首先要考虑对干扰进行消除。

在数字信号处理领域，常用的干扰消除的方法主要有滤波和平滑，而脉冲星信号本身就是一种脉冲，相对与数据采集与数据分析来说，其本身就是一种噪声，常用的滤波与平滑同时会对脉冲星的信号造成滤波或平滑作用，而脉冲星研究的本质就是通过研究脉冲星的轮廓来研究脉冲星的各项性质，要求在消除射电干扰的同时不能影响脉冲星本身的轮廓形状与特征。所以常用的滤波与平滑不能满足脉冲星观测的干扰消除要求。

目前国际上在脉冲星观测研究时域宽频射电干扰消除方法有：自适应滤波法；零色散通道积分、消除强干干扰法。

自适应滤波法为当前脉冲星观测中最有效的干扰剔除方法，但自适应滤波法需要复杂的硬件环境，需要两台望远镜、接收机和实时采集终端，两台望远镜分别为主望远镜和参考望远镜，这种方法有效，但是实现起来非常困难，首先需要建立复杂的硬件环境，同时自适应滤波算法需要反复的调试，目前只在澳大利亚Parkes天文台得到应用。

零色散通道积分、消除强干干扰法为目前脉冲星数据处理中消除宽频射电干扰的主要方法，该方法是利用通道零色散量积分，找出有干扰的时间点，然后利用前后时间点的数据进行插值替代该时间点的数据，但是，该方法在消除射电干扰的同时也一定程度的影响了脉冲星的轮廓形状。

因此，本领域的专业技术人员需要迫切解决的技术问题就是：如何能创新的提出一种措施，在不影响脉冲星轮廓形状的同时消除时域宽频的射电干扰。

技术实现要素：

为了解决上述问题，消除较大色散的脉冲星在射电波段观测数据的时域干扰，获得更加真实的脉冲星轮廓及到达时间。本发明所采用的技术方案如下：一种消除脉冲星到达时间数据中宽频时域干扰的方法，包括以下步骤：

S1：观测脉冲星的脉冲信号；

利用射电望远镜接收来自宇宙空间中脉冲星信号，观测脉冲星到达时间，所述脉冲星信号经过射电望远镜聚焦后，通过高灵敏度接收机进行放大后混频后，进行数字化采集，在脉冲星观测中，由于脉冲星同时发出多种频率脉冲信号，所有脉冲信号经过星际空间传播以后，不同频率的信号到达地球的时间不同；

S2：得到脉冲星的周期性脉冲轮廓；

在宽频条件下，同时采集脉冲星信号的高频率分辨率、高时间分辨率数据，通过对通道进行色散延迟改正后进行周期叠加得到周期性的脉冲轮廓；

S3：对脉冲星的周期性脉冲轮廓进行消除色散延迟处理；

由于色散的作用，不消除不同频率信号延迟，将导致脉冲星的轮廓变形，或看不到脉冲星信号，脉冲星观测系统把接收到的宽频信号分成多个通道，计算各个通道的电磁波延迟，扣除各个通道的信号延迟后，再进行通道叠加，即实现对脉冲星的周期性脉冲轮廓进行消除色散延迟处理；

S4：观测脉冲星脉冲信号数据中的宽频射电干扰；

对脉冲星的周期性脉冲轮廓进行消除色散延迟处理后，在有脉冲信号的地方有很多射电干扰，射电干扰叠加在脉冲信号上，对脉冲星的轮廓和到达时间造成严重的影响；

S5：消除脉冲星到达时间数据中的宽频时域干扰；

利用脉冲星的色散延迟的特性，通过干扰消除算法，消除脉冲星到达时间数据中的宽频时域干扰。

进一步的，所述步骤S2包括：

S21：天文接收机接收通过宇宙空间的星际介质的脉冲星信号，将脉冲星信号的频率带宽Δf内的信号放大、降频到中频；

S22：使用中频电缆将中频信号注入到终端系统，终端系统把频率带宽为Δf的信号分成v₁、v₂、v₃.....v_n n个子通道，每个子通道带宽为Δf/n；

S23：以子通道v_n/2为基准，计算子通道v₁、v₂、v₃.....v_n对子通道v_n/2的时间延迟Δt₁、Δt₂、Δt₃......Δt_n；

S24：改正每个子通道的时间延迟，对每个子通道的数据进行叠加，获得脉冲星的轮廓。

进一步的，所述宇宙空间的星际介质的作用为对脉冲星的脉冲信号造成延迟。

进一步的，步骤S5所述干扰消除算法包括：

在实际观测中，每次采样记录的数值记为p_ij，其中i为通道序号，范围为0～n，j为采样序号，脉冲星的周期为T，采样率为Δτ，一个周期的采用点数为T/Δτ。

S51：通道改正

对n个子通道的T/Δτ次采样的数据进行归一化，改正n个子通道数据的系统相应及高频衰减，计算每个通道的功率响应，对通道的周期点数进行算数平均，以任意一个通道的平均功率响应为基准进行通道改正，重新计算每个通道的每次采样的数值p′_ij；

S52：计算色散延迟与脉冲星轮廓宽度

通过色散延迟时间公式计算整个带宽内的色散延迟时间，通过脉冲星星表获得脉冲星的标准轮廓，或利用历史数据的标准轮廓计算出脉冲星的轮廓宽度W_psr；

S53：干扰消除

计算脉冲星的通道数据采样点的值，所述采样点的值包括：脉冲星信号值、射电干扰值、系统噪声值，所述脉冲星信号值只在有脉冲星脉冲辐射的地方存在，所述射电干扰值为随机干扰噪声值，所述系统噪声在整个周期内都存在；

如果色散延迟时间Δt＞2W_psr，在脉冲星的周期为T内，第i通道有脉冲星信号，即第i通道的通道数据采样点的值包括：脉冲星信号值、射电干扰值、系统噪声值，则第i+n/2通道没有脉冲星信号，及第i+n/2通道的通道数据采样点的值包括：射电干扰值、系统噪声值；

将第i通道的通道数据采样点的值减去第i+n/2通道的通道数据采样点的值即得到脉冲星信号值。

进一步的，所述轮廓宽度W_psr为信号两边边缘的相位宽度。

更进一步的，所述色散延迟时间公式为：Vt＝4.148808DM[(v₀)^-2-(v_n)^-2]，式中DM为脉冲星色散量，单位为秒差距每立方厘米，所述秒差距是天文学上的一种长度单位，1秒差距等于3.2615637769744079138光年，v₀、v_n为频率，单位GHz。

相比于现有技术，本发明的有益效果为：

本发明利用宽频时域干扰的相关性，通过通道相减消除宽频的时域干扰消除脉冲星观测数据中的宽频时域干扰，获得真实的脉冲星轮廓，提高脉冲星到达时间的精度，为脉冲星的到达时间观测研究提供更可靠的保障。

附图说明

图1为本发明的消除脉冲星到达时间数据中宽频时域干扰的方法流程图；

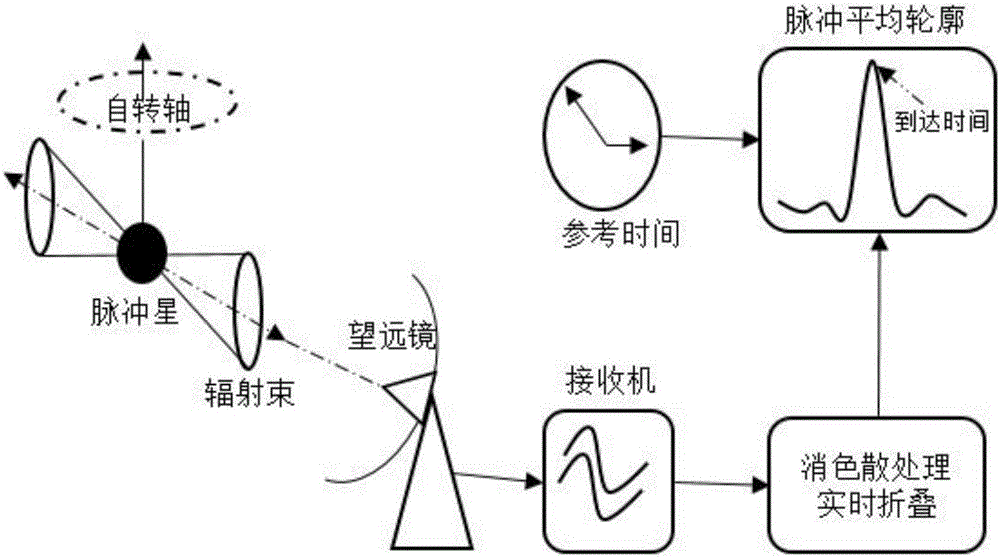
图2为本发明的观测脉冲星的脉冲信号原理图；

图3为本发明的脉冲星脉冲到达时间随频率变化图；

图4为本发明的得到脉冲星的周期性脉冲轮廓原理图；

图5为本发明的没有消除色散延迟时的脉冲星轮廓及时域干扰图；

图6为本发明的消除色散后的脉冲星轮廓及时域干扰图；

图7为本发明的计算脉冲轮廓宽度示意图；

图8本发明的实施例中没有消除色散延迟时的脉冲星轮廓及时域干扰图；

图9为本发明的实施例中消色散但没有消除干扰后的脉冲星的轮廓图；

图10为本发明的实施例中消除时域干扰后真实的脉冲星轮廓图；

图11为本发明的实施例中消除时域干扰后用系统白噪声替代负值脉冲轮廓后真实的脉冲星轮廓图。

具体实施方式

下面结合具体实施例对本发明进一步进行描述。

如图1所示，本发明提供了一种消除脉冲星到达时间数据中宽频时域干扰的方法，包括以下步骤：

S1：观测脉冲星的脉冲信号；

如图2所示，利用射电望远镜接收来自宇宙空间中脉冲星信号，观测脉冲星到达时间，所述脉冲星信号经过射电望远镜聚焦后，通过高灵敏度接收机进行放大后混频后，进行数字化采集。

如图3所示，在脉冲星观测中，由于脉冲星同时发出多种频率脉冲信号，所有脉冲信号经过星际空间传播以后，不同频率的信号到达地球的时间不同，图3中纵坐标为通道，不同的通道为不同的频率，高频通道的信号相对低频通道的信号先到达观测站。

S2：得到脉冲星的周期性脉冲轮廓；

如图4所示，在宽频条件下，同时采集脉冲星信号的高频率分辨率、高时间分辨率数据，通过对通道进行色散延迟改正后进行周期叠加得到周期性的脉冲轮廓；从图4中可以发现，脉冲信号非常强，同时在有脉冲信号的地方有很多射电干扰，这些干扰叠加在脉冲信号上，将对脉冲星的轮廓和到达时间造成严重的影响，特别是高精度的脉冲星到达时间观测研究及脉冲星辐射机制研究。

脉冲星观测系统原理如图4所示，脉冲星的信号通过宇宙空间的星际介质(ISM)后，ISM的作用对脉冲星的脉冲星信号造成延迟，经过天文接收机后将频率带宽为Δf将信号放大、降频到中频，经过中频电缆注入到终端系统，终端系统把频率带宽为Δf的信号分成v₁、v₂、v₃.....v_n n个子通道，每个子通道带宽为Δf/n。以v_n/2子通道为基准，计算v₁、v₂、v₃.....v_n每个子通道对v_n/2通道的时间延迟Δt₁、Δt₂、Δt₃......Δt_n，改正每个通道的时间延迟后对每个通道的数据进行叠加，从而获得脉冲星的轮廓。

S3：对脉冲星的周期性脉冲轮廓进行消除色散延迟处理；

由于色散的作用，不消除不同频率信号延迟，将导致脉冲星的轮廓变形，或看不到脉冲星信号，脉冲星观测系统把接收到的宽频信号分成多个通道，计算各个通道的电磁波延迟，扣除各个通道的信号延迟后，再进行通道叠加，即实现对脉冲星的周期性脉冲轮廓进行消除色散延迟处理。如图5所示，消除色散延迟后获得了非常强的脉冲星脉冲信号。

S4：观测脉冲星脉冲信号数据中的宽频射电干扰；

对脉冲星的周期性脉冲轮廓进行消除色散延迟处理后，在有脉冲信号的地方有很多射电干扰，射电干扰叠加在脉冲信号上，对脉冲星的轮廓和到达时间造成严重的影响；

S5：消除脉冲星到达时间数据中的宽频时域干扰；

利用脉冲星的色散延迟的特性，通过干扰消除算法，消除脉冲星到达时间数据中的宽频时域干扰。

脉冲星色散的大小与脉冲星的距离相关，距离越远其色散值越大，色散的表达公式如下：

$DM=\underset{0}{\overset{d}{\∫}}{n}_{e}dl---\left(1\right)$

其中DM为脉冲星色散、l为脉冲的距离、n_e为银河系平均电子密度。

不同频率电磁波通过星际空间后时间延迟可以表达为：

Vt＝4.148808DM[(v₀)^-2-(v₁)^-2] (2)

其中Vt为不同频率信号的到达地球接收器时间延迟，单位为毫秒，DM为脉冲星色散量，单位为秒差距每立方厘米，秒差距是天文学上的一种长度单位，1秒差距等于3.2615637769744079138光年，v₀、v₁为频率，单位GHz。

脉冲星观测数据消干扰目的是消除脉冲星观测频段范围内的窄带干扰和宽频时域干扰。通常消除脉冲星干扰的方法是，通过一定的算法找到干扰的通道或时域上干扰的点，频域上的干扰消除通道的数据，时域上是采用本地的值加上rms的随机噪声替代时域上的干扰点，这种方法可以消除干扰的通道和干扰的数据，获得较好的轮廓，但是，如果干扰叠加在脉冲星的轮廓上，此时该时刻的值应该是：

T_sig＝T_sys+T_psr+T_rfi (3)

式中：T_sig总信号强度，T_psr脉冲星的信号，T_sys为系统噪声，T_rfi为射电干扰。

为了消除干扰的影响，而采用系统噪声的值替代这个时刻的采样值，这个时刻的值设置为系统噪声，也就是T_sig～＝T_sys，损失了脉冲星的辐射功率，这将提高脉冲星的到达时间噪声，同时会改变脉冲星的辐射轮廓，从而影响脉冲星的到达时间的精度，对脉冲星的辐射机制研究造成影响。

在本发明中，记录每次观测采样的数值为p_ij，i为通道序号，范围为

0～n,j为采样序号。脉冲星的周期为T，采样率为Δτ，一个周期的采用点数为T/Δτ。

所述步骤S5包括：

S51：通道改正

对n个子通道的T/Δτ次采样的数据进行归一化，改正n个子通道数据的系统相应及高频衰减，计算每个通道的功率响应，对通道的周期点数进行算数平均，计算公式为：

$\stackrel{\‾}{p_i}=\frac{\underset{1}{\overset{T/\mathrm{\Δ}\mathrm{\τ}}{\Σ}}{p}_{ij}}{\frac{T}{\mathrm{\Δ}\mathrm{\τ}}}---\left(4\right)$

以任意一个通道的平均功率响应为基准进行通道改正，重新计算每个通道的每次采样的数值p′_ij；如以第k通道为基准，则：

$p_{ij}^{\′}=\frac{{\stackrel{\‾}{p}}_k{p}_{ij}}{{\stackrel{\‾}{p}}_i}---\left(5\right)$

S52：计算色散延迟与脉冲星轮廓宽度

通过色散延迟时间公式计算整个带宽内的色散延迟时间，由公式(2)可得：

Vt＝4.148808DM[(v₀)^-2-(v_n)^-2] (6)

通过脉冲星星表获得脉冲星的标准轮廓，或利用历史数据的标准轮廓计算出脉冲星的轮廓宽度W_psr；脉冲轮廓宽度为信号两边边缘的相位宽度。

如图7所示，轮廓开始于0.485，结束于0.519，相对宽度为：(0.519-0.485)×T＝0.034T，T为脉冲星的周期。

S53：干扰消除

在本发明中，利用脉冲星的色散延迟的特性，不同频率的脉冲星的信号到达时间不一样，高频的信号先到达，低频的后到达，记高频信号的到达时刻为t_psr-h，低频信号的到达时刻为t_psr-l，则t_psr-h＜t_psr-l，而干扰信号同一时间到达，t_rfi-h＝t_rfi-l，通过计算脉冲星的辐射轮廓与脉冲星的观测带宽的延迟，如果脉冲星在观测带宽内色散延迟大于两倍的脉冲星带宽Δt＝t_psr-l-t_psr-h＞2W_psr，通过通道校准后，通道交差相减可以有效消除宽频的射电干扰，而不影响脉冲星的信号。

由公式(3)可计算脉冲星的通道数据采样点的值：

$P_{ij}\∝T_{ij}^{sys}+T_{ij}^{psr}+T_{ij}^{rfi}---\left(7\right)$

其中为系统噪声，整个周期都存在；脉冲星信号，只在有脉冲辐射的地方有信号，为射电干扰，为随机干扰噪声。

脉冲星的通道数据采样点的值包括以下几种情况：

(1)没有脉冲信号和干扰采样：

$P_{ij}\∝T_{ij}^{sys}---\left(8\right)$

(2)没有脉冲信号、有干扰的采样：

$P_{ij}\∝T_{ij}^{sys}+T_{ij}^{rfi}---\left(9\right)$

(3)有脉冲星信号、没有干扰的采样：

$P_{ij}\∝T_{ij}^{sys}+T_{ij}^{psr}---\left(10\right)$

(4)有脉冲星信号、有干扰的采样：

$P_{ij}\∝T_{ij}^{sys}+T_{ij}^{psr}+T_{ij}^{rfi}---\left(11\right)$

由于脉冲星的信号随不同频率有时间延迟，当Δt＞2W_psr时，第i通道有脉冲星信号时其采样数据为：

或

而第i_+n2通道没有脉冲信号，其采样数据为：

或

不同的通道之间，通过通道改正之后有：

$T_{ij}^{sys}=T_{(i+n/2)j}^{sys},T_{ij}^{rfi}=T_{(i+n/2)j}^{rfi}$

那么i通道与i+n/2通道相减后只保留了脉冲星信号与系统的白噪声

$p_{ij}-p_{(i+n/2)j}\∝T_{ij}^{psr}$

最后对相减后得到脉冲星负值的轮廓，用系统的白噪声范围的随机数进行替代。

所以，可以得到下述结论：如果色散延迟时间Δt＞2W_psr，在脉冲星的周期为T内，第i通道有脉冲星信号，即第i通道的通道数据采样点的值包括：脉冲星信号值、射电干扰值、系统噪声值，则第i+n/2通道没有脉冲星信号，及第i+n/2通道的通道数据采样点的值包括：射电干扰值、系统噪声值，将第i通道的通道数据采样点的值减去第i+n/2通道的通道数据采样点的值即得到脉冲星信号值。

所以对色散延迟满足Δt＞2W_psr的脉冲星可以对改正后的通道数据进行相减，非常有效的消除射电干扰的同时保留脉冲星的信号。

本发明在实际应用中，对脉冲星PSR J1645-0317的实测数据进行了处理。图8表示由于色散延迟，没有消除色散延迟及时域干扰的脉冲轮廓；图9表示消色散但没有消除干扰后脉冲轮廓；图10表示消除时域干扰后脉冲轮廓，图11表示消除时域干扰后，用系统白噪声替代负值脉冲轮廓后真实的脉冲星轮廓。从图8中可以看出，脉冲星的信号受色散延迟和时域干扰的影响，导致脉冲轮廓变形，或者看不到脉冲星信号；从图9可以看出，消除色散延迟后获得了非常强的脉冲信号，但脉冲轮廓及本底上有许多干扰；从图11、图10与图8、图9的对比可以看出本发明可以非常好的的消除时域上的干扰获得真实的脉冲轮廓。

以上对本发明所提供的一种消除脉冲星到达时间数据中宽频时域干扰的方法进行了详细介绍，本文中应用了具体个例对本发明的原理及实施方式进行了阐述，以上实施例的说明只是用于帮助理解本发明的方法及其核心思想；同时，对于本领域的一般技术人员，依据本发明的思想，在具体实施方式及应用范围上均会有改变之处，综上所述，本说明书内容不应理解为对本发明的限制。

最后应说明的是：以上所述仅为本发明的优选实施例而已，并不用于限制本发明，尽管参照前述实施例对本发明进行了详细的说明，对于本领域的技术人员来说，其依然可以对前述各实施例所记载的技术方案进行修改，或者对其中部分技术特征进行等同替换,凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。