一种超级电容非线性三分支等效电路模型及参数辨识方法与流程

本发明属于超级电容器的建模及其参数辨识领域，具体涉及一种超级电容非线性三分支等效电路模型及参数辨识方法。
背景技术：
：超级电容器在新能源领域表现出了朝阳产业趋势，许多发达国家都已经把超级电容器项目作为国家重点研究和开发项目，超级电容器的国内外市场正呈现出前所未有的蓬勃景象。目前，超级电容器的潜力已经得到越来越多的关注。而在为超级电容器设计性能良好地能量均衡装置以及其他超级电容器的重要应用中，均需要通过反复的电路仿真和参数优化来得到最佳的设计方案，其中，最基础同时也最关键的一环就是需要一个精确的超级电容器模型。然而世界各国对超级电容器的研究还处于基础阶段，超级电容器与传统的电池有着很大的不同，而我们对超级电容器的使用和研究仅仅是停留在对传统电池的认识的基础上。超级电容器与其他类型的动力电池相比较，具有无可比拟的优势。但我们对超级电容器性能的研究还不够透彻，在现有的超级电容器技术的基础上，对超级电容器的应用与管理还有很大的改善空间。建立一个可以准确描述超级电容器动态特性的模型是超级电容器研究的热点问题。现今对超级电容器的建模有多种多样，主要有等效电路建模、人工神经网络建模、多孔电极传输线建模等，但其实用性和精确性往往不容乐观，不仅不能对超级电容器管理系统的实际设计提供帮助，还浪费了设计人员大量的时间和精力。普通等效电路模型不能很好的表征超级电容器独特的电气特性、参数辨识难度大。极小化实际系统与模型之间的误差的方法有很多种，这类辨识方法根据其基本原理的不同，可以分为三种类型。第一类成为梯度校正法，在确定性问题中，如果过程的输入输出含有噪声，梯度校正法就不能用。而在随机性问题中，事先必须知道噪声的一阶矩和二阶矩统计特性。第二类方法被称为极大似然法，极大似然法最大的缺点是要先知道分布形式，并且极大似然函数通常是很难救解的，极大似然法运算太复杂。第三类是最小二乘法，它的原则是让实测数据和估计数据之间的距离平方和最小。它的核心原理是通过最小化误差的平方和来寻找最佳的参数估计值。最小二乘法，它既可以应用在线性数学模型上也可以应用在非线性数学模型上。最小二乘法的应用非常广泛，在很多领域是通用的。技术实现要素：：为了克服上述
背景技术：
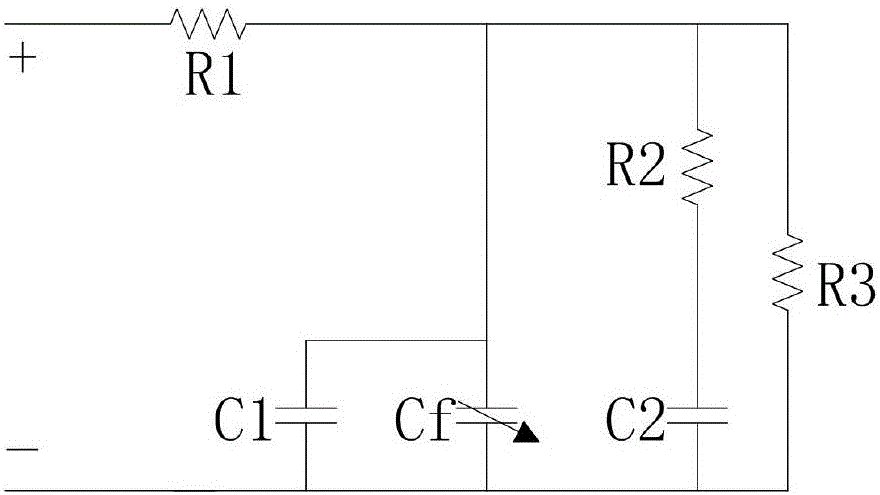
的缺陷，本发明提供一种超级电容非线性三分支等效电路模型及参数辨识方法，精确性高,实用性强，方便在实际中进行工程应用。为了解决上述技术问题本发明的所采用的技术方案为：一种超级电容非线性三分支等效电路模型的参数辨识方法，建立超级电容非线性三分支等效电路模型，超级电容非线性三分支等效电路模型包括从正极端到负极端依次串联的等效串联电阻R1和三条并联的支路，三条并联的支路包括自放电电阻R3支路、瞬时支路和长时间支路；瞬时支路包括并联的电容C1和可变电容Cf，可变电容Cf的电容值随超级电容器端电压的变化而变化；长时间支路包括串联的电阻R2和电容C2；对超级电容进行充放电实验，并由实验所得的实验数据获取等效电路模型的模型参数，实验数据包括每次充放电实验期间超级电容的端电压、充电电流和充电时间。较佳地，依据实验数据运用电路分析法得到模型参数等效串联电阻R1和自放电电阻R3的值；依据实验数据和等效串联电阻R1的值利用最小二乘法对模型进行估算，辨识模型参数并联的电容C1和可变电容Cf的值获取长时间支路的电阻R2和电容C2的值。较佳地，等效串联电阻其中，UC(t)1为加载恒定电流Ix之前的超级电容的端电压，UC(t)2为超级电容器加载恒定电流Ix后的瞬间端电压。较佳地，自放电电阻其中，UC(t)3为超级电容器充满电后内部达到电荷平衡时的端电压，UC(t)4为超级电容器静置自放电时间ta后的端电压，ta为超级电容器的一段自放电时间，C为超级电容器的标称电容值。较佳地，电容其中，UC(ti)为ti时刻超级电容器的端电压，i＝1,2,…N，N为充放电实验次数，Ii为第i次充电电流，tni为第i次充电时间，UC(0)为充电前t＝0时刻的超级电容器的端电压。较佳地，Cf(t)＝aUc(t)，其中，UC(t)为t时刻超级电容器的端电压，N为充放电实验次数，Ii为第i次充电电流，tni为第i次充电时间，UC(0)为充电前t＝0时刻的超级电容器的端电压。较佳地，电容其中UC2(0)超级电容器充电之前电压初始值，UC1(0)为超级电容器充电完成之时、电压自调整之前的端电压，UC1(t)为超级电容器充电后完成电压自调整时的端电压。较佳地，电阻其中UC2(0)超级电容器充电之前电压初始值，UC1(0)为超级电容器充电完成之时、电压自调整之前的端电压，UC1(t)为超级电容器充电后完成电压自调整时的端电压，Δt为超级电容器充电后的电压自调整时间。本发明还提供一种超级电容非线性三分支等效电路模型，超级电容非线性三分支等效电路模型包括从正极端到负极端依次串联的等效串联电阻R1和三条并联的支路，三条并联的支路包括自放电电阻R3支路、瞬时支路和长时间支路；瞬时支路包括并联的电容C1和可变电容Cf，可变电容Cf的电容值随超级电容器端电压的变化而变化；长时间支路包括串联的电阻R2和电容C2。本发明的有益效果在于：本模型及参数辨识方法能可靠的反映超级电容器的实际工作状态和性能表现。可以在更长时间范围内很好的体现超级电容器的外部电气特性，并且参数的选择尽量精简，使参数的辨识能够实现，精确性高,实用性强，方便在实际中进行工程应用。附图说明图1本发明实施例一非线性三分支等效电路模型；图2本发明实施例一超级电容器自放电等效电路图；图3本发明实施例一超级电容器短期充放电条件下的等效电路图；图4本发明实施例一超级电容器内部电荷自调整等效电路图；图5本发明实施例二超级电容器的建模及其参数辨识的流程图；图6本发明实施例二超级电容器实测电压曲线和模型仿真电压曲线。具体实施方式下面结合附图和实施例对本发明做进一步的说明。实施例一一种超级电容非线性三分支等效电路模型，如图1所示，超级电容非线性三分支等效电路模型包括从正极端到负极端依次串联的等效串联电阻R1和三条并联的支路，三条并联的支路包括自放电电阻R3支路、瞬时支路和长时间支路；瞬时支路包括并联的电容C1和可变电容Cf，可变电容Cf的电容值随超级电容器端电压的变化而变化；长时间支路包括串联的电阻R2和电容C2。实施例二一种超级电容非线性三分支等效电路模型的参数辨识方法，包括：建立超级电容非线性三分支等效电路模型对超级电容进行充放电实验，并由实验所得的实验数据获取等效电路模型的模型参数，实验数据包括每次充放电实验期间超级电容的端电压、充电电流和充电时间。如图2所示，具体包括如下步骤：步骤1，建立超级电容非线性三分支等效电路模型，超级电容非线性三分支等效电路模型与实施例一相同。如图1所示，超级电容非线性三分支等效电路模型包括从正极端到负极端依次串联的等效串联电阻R1和三条并联的支路，三条并联的支路包括自放电电阻R3支路、瞬时支路和长时间支路；瞬时支路包括并联的电容C1和可变电容Cf，可变电容Cf的电容值随超级电容器端电压的变化而变化；长时间支路包括串联的电阻R2和电容C2。步骤2，对超级电容进行充放电实验，并由实验所得的实验数据获取等效电路模型的模型参数，实验数据包括每次充放电实验期间超级电容的端电压、充电电流和充电时间；在室温条件下，在测试平台上对超级电容器实物进行多次充放电实验，记录其每次实验期间超级电容器的端电压、充电电流、充电时间。本测试研究对象基于超级电容器模块:由两个BMOD0165-P048超级电容器并联，其标称电容值为330F，输出电压范围为20-48.5V,输出电流范围0-100A。实验步骤如下：(1)静置超级电容器超过5个小时，让超级电容器内部达到充分的内部电荷平衡状态。(2)以10A电流对超级电容器充电，直到超级电容器端电压达到48.5V，停止充电，再以10A电流对超级电容器放电，直到超级电容器端电压下降到20V，停止放电，此时测量超级电容器的初始端电压为20v(3)以20A电流对超级电容器充电，直到超级电容器端电压达到48.5V，停止充电，记录充电时间t1。(4)以20A电流对超级电容器放电，直到超级电容器端电压下降到20V，停止放电，以30A电流对超级电容器充电，直到超级电容器端电压达到48.5V，停止充电，记录充电时间t2。(5)以30A电流对超级电容器放电，直到超级电容器端电压下降到20V，停止放电，以40A电流对超级电容器充电，直到超级电容器端电压达到48.5V，停止充电，记录充电时间t3。(6)以40A电流对超级电容器放电，直到超级电容器端电压下降到20V，停止放电，以50A电流对超级电容器充电，直到超级电容器端电压达到48.5V，停止充电，记录充电时间t4。(7)以50A电流对超级电容器放电，直到超级电容器端电压下降到20V，停止放电，以60A电流对超级电容器充电，直到超级电容器端电压达到48.5V，停止充电，记录充电时间t5。(8)以60A电流对超级电容器放电，直到超级电容器端电压下降到20V，停止放电，以70A电流对超级电容器充电，直到超级电容器端电压达到48.5V，停止充电，记录充电时间t6。(9)以70A电流对超级电容器放电，直到超级电容器端电压下降到20V，停止放电，以80A电流对超级电容器充电，直到超级电容器端电压达到48.5V，停止充电，记录充电时间t7。(10)以80A电流对超级电容器放电，直到超级电容器端电压下降到20V，停止放电，以90A电流对超级电容器充电，直到超级电容器端电压达到48.5V，停止充电，记录充电时间t8。(11)以90A电流对超级电容器放电，直到超级电容器端电压下降到20V，停止放电，以100A电流对超级电容器充电，直到超级电容器端电压达到48.5V，停止充电，记录充电时间t9。表1为进行9次充放电实验也即N＝9组不同的恒定充电电流下超级电容器从初始电压UC(0)＝20V变化到终止电压UC(ti)＝48.5V的充电时间。表1在不同电流下充电时间步骤3，依据实验数据运用电路分析法得到模型参数等效串联电阻R1和自放电电阻R3的值；等效串联电阻其中，UC(t)1为加载恒定电流Ix之前的超级电容的端电压，UC(t)2为超级电容器加载恒定电流Ix后的瞬间端电压。自放电电阻其中，UC(t)3为超级电容器充满电后内部达到电荷平衡时的端电压，UC(t)4为超级电容器静置自放电时间ta后的端电压，ta为超级电容器的一段自放电时间，C为超级电容器的标称电容值。具体地，参数R1：超级电容器非线性三分支等效电路模型中R1为超级电容器等效串联内阻。R1可通过对超级电容器加载电压瞬间端电压的跳变情况得出。在实验室条件下，超级电容器静置足够长时间后，加载电流Ix＝10A瞬间，流过超级电容器的电流由0突变成恒定电流Ix＝10A。加载电流之前，超级电容器端电压UC(t)1可以认为是开路电压，输入恒定电流Ix之前测得UC(t)1＝20V，加载电流后瞬间，测得超级电容器端电压UC(t)2＝20.41V，超级电容器内部流过电流Ix。由于欧姆内阻影响，超级电容器端电压UC(t)2＝R1Ix+UC(t)1，由此可计算出超级电容器串联等效电阻其中Ix为加载电流，UC(t)1为加载电流前超级电容器的端电压，UC(t)2为加载电流后瞬间超级电容器的端电压，代入数据得出R1＝0.041Ω。参数R3：超级电容器非线性三分支等效电路模型的第三支路为R3支路，电阻R3为超级电容器的自放电电阻。超级电容器自放电等效电路如图2所示,其中C可认为是本测试超级电容器的标称电容值330F。超级电容器充满电后，断开超级电容器充放电电流，并静置2小时使超级电容器内部达到电荷的平衡，测得超级电容器电压UC(t)3＝48.4V。再次静置超级电容器24小时，测量超级电容器电压UC(t)4＝47.4V。根据KVL可得由超级电容器在ta＝24h时间内从电压UC(t)3自放电到电压UC(t)4，于是得得其中UC(t)3为超级电容器充满电后内部达到电荷平衡时的端电压，UC(t)4为超级电容器静置一段时间ta后的端电压，ta为超级电容器的一段自放电时间。C为超级电容器的标称电容值。可求得超级电容器自放电内阻R3＝12.6KΩ。步骤4，依据实验数据和等效串联电阻R1的值利用最小二乘法对模型进行估算，辨识模型参数并联的电容C1和可变电容Cf的值电容其中，UC(ti)为ti时刻超级电容器的端电压，i＝1,2,…N，N为充放电实验次数，Ii为第i次充电电流，tni为第i次充电时间，UC(0)为充电前t＝0时刻的超级电容器的端电压。Cf(t)＝aUc(t)，其中，UC(t)为t时刻超级电容器的端电压，N为充放电实验次数，Ii为第i次充电电流，tni为第i次充电时间，UC(0)为充电前t＝0时刻的超级电容器的端电压。具体的说，先对模型电路进行分析，第一支路为瞬时支路，由不变电容C1、时变电容Cf组成，Cf(t)是一个随着端电压变化而改变的可变电容，它反映了端电压变化对超级电容器产生的影响，Cf(t)满足式(1)。Cf(t)＝f(Uc(t))(1)其中UC(t)为超级电容器t时刻的端电压。当开始对超级电容器充电时，电流主要经过瞬时支路，通过电阻R1对电容C1和Cf充电，此时，超级电容器的总的等效电容值为Ctotal。Ctotal＝C1+Cf(2)由(1)代入(2)可得：Ctotal＝C1+f(Uc(t))(3)在超级电容器的动态过程中，超级电容器等效电容的总值与端电压满足线性关系，满足式(4)。Ctotal＝C1+aUc(t)(4)由式(4)可知：f(Uc(t))＝aUc(t)(5)Cf(t)＝aUc(t)(6)其中UC(t)为t时刻超级电容器的端电压。由图3得t时刻模型的超级电容器端电压UC(t)为：设则r＝C1+aUc(t)则由公式(9)得其中i＝1,2,…N。其中Ii为步骤二中实验所记录的第i次充电电流，tni为步骤二中实验所记录的第i次充电时间。UC(0)为充电前t＝0时刻的超级电容器的端电压。UC(ti)为ti时刻超级电容器的端电压。由R1、UC(ti)、UC(0)和Ii、tni的值根据公式(10)可求出ri的值，其中i＝1,2,…N。下面用最小二乘法求出C1、a。令最小二乘法原理就是求出使M取得最小值时的C1、a。如果把M看作是自变量为C1、a的函数，有多元函数取最值的条件可知，上述问题可以通过求方程组的解来解决，即令整理得则参数C1、a的最小二乘估计为：其中UC(ti)为ti时刻超级电容器的端电压，i＝1,2,…N。由ti时刻超级电容器的端电压UC(ti)、实验次数N、ri，根据公式(11)、(12)在Matlab环境下经过仿真运算可得a＝0.32，C1＝328.07F，再由式(6)得Cf＝0.32UC，UC为超级电容器的端电压。步骤5，获取长时间支路的电阻R2和电容C2的值。电容其中UC2(0)超级电容器充电之前电压初始值，UC1(0)为超级电容器充电完成之时、电压自调整之前的端电压，UC1(t)为超级电容器充电后完成电压自调整时的端电压。电阻其中UC2(0)超级电容器充电之前电压初始值，UC1(0)为超级电容器充电完成之时、电压自调整之前的端电压，UC1(t)为超级电容器充电后完成电压自调整时的端电压，Δt为超级电容器充电后的电压自调整时间。对模型电路进行分析，超级电容器内部电荷自调整等效电路如图4所示。取刚充电完成之时、电压自调整之前等效电容C1端电压为UC1(0)，即此时超级电容器的端电压。等效电容C2的初始电压为超级电容器充电之前电压初始值，取为UC2(0)。充电后经过Δt时间完成电压自调整，此时C1端电压为UC1(t)，即此时超级电容器的端电压。即UC2(0)超级电容器充电之前电压初始值，UC1(0)为超级电容器充电完成之时、电压自调整之前的端电压，UC1(t)为超级电容器充电后完成电压自调整时的端电压。Δt为超级电容器充电后的电压自调整时间。在电压自调整期间，内部的电荷总量不变，可得式(13)：Q0＝Qt(13)式中Q0为超级电容器内部调整之前总电荷，Qt为电压自调整之后总电荷。由此可得：(C1+Cf(0))UC1(0)+C2UC2(0)＝(C1+Cf(t)+C2)UC1(t)(14)由式(6)可得：(C1+aUC1(0))UC1(0)+C2UC2(0)＝(C1+aUC1(t)+C2)UC1(t)所以得：其中UC2(0)超级电容器充电之前电压初始值，UC1(0)为超级电容器充电完成之时、电压自调整之前的端电压，UC1(t)为超级电容器充电后完成电压自调整时的端电压。其中UC1(0)、UC2(0)、UC1(t)、C1均为已知数，故可得到超级电容器等效电容C2。在超级电容器内部自调整开始瞬间，由于超级电容器等效电容足够大，可以认为端电压Uc1为一定值。根据基尔霍夫电压定律，可得：UC1(0)＝iR2+UC2(0)(16)其中，电流i为超级电容器自调整开始时，内部自调整电流，把式(16)和式(6)代入式(17)中，得：由超级电容器充电后静置电压随时间变化大小可知超级电容器的等效电阻R2可由此得出：其中UC2(0)超级电容器充电之前电压初始值，UC1(0)为超级电容器充电完成之时、电压自调整之前的端电压，UC1(t)为超级电容器充电后完成电压自调整时的端电压。Δt为超级电容器充电后的电压自调整时间。对超级电容器充放电使其端电压达到额定电压的70％，即34V，此时UC2(0)＝34V。然后对其充电使其端电压达到48.5V，此时UC1(0)＝48.5V。再将其静置经过时间Δt＝713s之后，超级电容器完成内部电荷自调整，此时测得其端电压为47.5V，此时UC1(t)＝47.5V。根据以上对超级电容器充放电实验所得的数据，分别由式(15)和式(19)得C2＝26.63F,R2＝30.09Ω。最后得非线性三分支等效电路模型模型参数如下表所示，参数数值R1/Ω0.041R2/Ω30.09R3/KΩ12.6C1/F328.07Cf/F0.32UcC2/F26.63表2非线性三分支等效电路模型模型参数辨识结果在得出的参数基础上，在SIMULINK中建立超级电容器非线性三分支等效电路模型，对超级电容器在SIMULINK中进行非线性三分支等效电路模型仿真，对超级电容器实物在测试平台上进行恒流充放电测试。充放电电流大小依次从20A变化到50A，使超级电容器在20V到48.5的电压范围内工作，电压采样周期为1s，工作时间为2457s。得到超级电容器实测电压曲线和模型仿真电压曲线如图6所示。对图6中的在SIMULINK环境下建立超级电容器的非线性三分支等效电路模型进行仿真得到的数据和在测试台架上对实物测得的数据进行比较分析，得到非线性三分支模型仿真误差如表3所示。项目模型误差电压误差范围(V)-2.037～1.322最大相对误差(％)4.24表3非线性三分支模型仿真误差从图6我们可以看出，非线性三分支等效电路模型能很好的跟随超级电容器的实际电压变化，在整体上，非线性三分支等效电路仿真模型与实际电压值拟合度高。从表3我们可以很明显的看出非线性三分支等效电路模型的电压与超级电容器的实际电压误差非常小，非线性三分支等效电路模型能够精确的反映超级电容器的电压变化。本发明利用电路分析法和最小二乘法对模型进行参数辨识，运用最小二乘法辨识的超级电容器非线性三分支等效电路模型能可靠性比较高的反映超级电容器的实际工作状态和性能表现。非线性三分支等效电路模型对超级电容器的仿真可靠性高、精确性高、实用性强，适合在工程上运用。应当理解的是，对本领域普通技术人员来说，可以根据上述说明加以改进或变换，而所有这些改进和变换都应属于本发明所附权利要求的保护范围。当前第1页1 2 3