一种应用于星基增强系统的星历星钟改正参数及空间信号完好性参数方法与流程

本发明属于卫星导航领域，具体地说，是一种应用于星基增强系统的星历星钟改正参数及空间信号完好性参数方法。

背景技术：

现有的单频星基增强系统(SBAS)主要面向民航用户，基于广泛布设的地面观测网监测全球导航卫星系统(GNSS)并生成星历星钟改正数和伪距改正数，以及对应的空间信号完好性参数等增强信息，通过SBAS卫星向大范围区域内用户广播这些增强信息，提升卫星导航服务的定位精度和完好性，进而提升服务连续性和可用性，使得卫星导航能够作为主用导航手段为民航提供服务。

SBAS的核心目标是增强卫星导航服务的完好性，在卫星导航服务不可用时，SBAS必须及时向服务区域内用户发出告警，因此SBAS系统段算法有完好性和实时性的约束：1)完好性：在计算改正参数的同时，必须给出相应的完好性参数，实现对改正误差的准确包络，确保用户保护级能够准确描述定位误差，从而实现对服务可用与否的准确判断；2)实时性：APV-II及CAT-I精密进近阶段对告警时间(从卫星发生故障到用户接收机发出告警所消耗的时间)的要求为6秒。为了满足告警时间的约束，主控站至少每秒执行一次系统段完好性监测算法，从而实现及时告警。

在完好性和实时性的约束下，GNSS所采用的基于精密动力学模型的定轨算法不再适用于SBAS，这是因为动力学模型过于复杂，难以实时计算，且这种算法难以给出完好性信息，不能用于完好性监测。为了满足完好性和实时性的要求，SBAS系统段算法主要利用基于码伪距的几何定轨法计算星历星钟改正参数和空间信号完好性参数，在观测条件较差时将出现星历星钟改正参数的改正精度较低的问题。

为了充分利用未来的北斗系统、伽利略系统等GNSS，以及位于L1和L5的双频民用信号，SBAS供应商正在制定双频多星座(DFMC)SBAS的接口控制文件。与单频SBAS相比，DFMC SBAS支持同时增强多达91颗卫星，在相同的下行带宽条件下，不播发与单频SBAS的快速改正数(最大更新周期为6秒)类似的伪距改正数，因此以往的星历星钟改正参数及对应的空间信号完好性参数算法不再适用，星历星钟改正参数及对应的空间信号完好性参数需要更为精确地估计和预测。

GNSS系统段根据长时段的历史观测数据，结合高精度的星历星钟模型，对未来的星历星钟值进行预测，并根据星历星钟预测值拟合得到广播电文的星历星钟模型参数。因此星历星钟误差包括了两部分，即星历星钟预测误差和广播电文拟合误差：星历星钟预测误差是指星历星钟预测值与真值之间的差值，由历史观测数据的观测误差和星历星钟模型的不精确性导致；广播电文拟合误差是指由广播电文参数计算得到的星历星钟值与星历星钟预测值之间的差值，由广播电文模型的不精确性导致。当前GPS卫星的URE均方根值约为2米，而星历星钟预测误差属于厘米级，因此广播电文拟合误差是星历星钟误差的主要来源。

技术实现要素：

本发明提出了一种应用于星基增强系统的星历星钟改正参数及空间信号完好性参数方法，该方法的核心思想是利用星历星钟预测值消除广播电文拟合误差，并利用实时观测量校正星历星钟预测误差，从而实现星历星钟改正参数及对应的空间信号完好性参数的准确估计。

本发明的一种应用于星基增强系统的星历星钟改正参数及空间信号完好性参数方法，包括以下几个步骤：

步骤一：获取实时观测量，并计算伪距残差；

步骤二：计算星历星钟先验误差；

步骤三：融合先验误差和实时伪距残差；

步骤四：对步骤三的融合结果进行卡尔曼滤波，得到星历星钟误差估计值；

步骤五：对星历星钟误差估计值进行拟合量化，从而得到星历星钟改正数广播值；

步骤六：计算使用星历星钟改正数广播值后的伪距残差；

步骤七：利用步骤六得到的伪距残差计算星历星钟协方差；

步骤八：分解步骤七得到的星历星钟协方差，并量化得到完好性参数广播值。

本发明的优点在于：

(1)本发明的星历星钟改正参数具有较高的改正精度；

(2)本发明的完好性参数对使用星历星钟改正数改正以后的伪距残差的包络更为准确；

(3)本发明提供的方法能够仅依赖于GPS系统就基本满足一类精密进近服务的需求。

附图说明

图1是本发明提供的星历星钟改正参数及空间信号完好性参数算法的流程图；

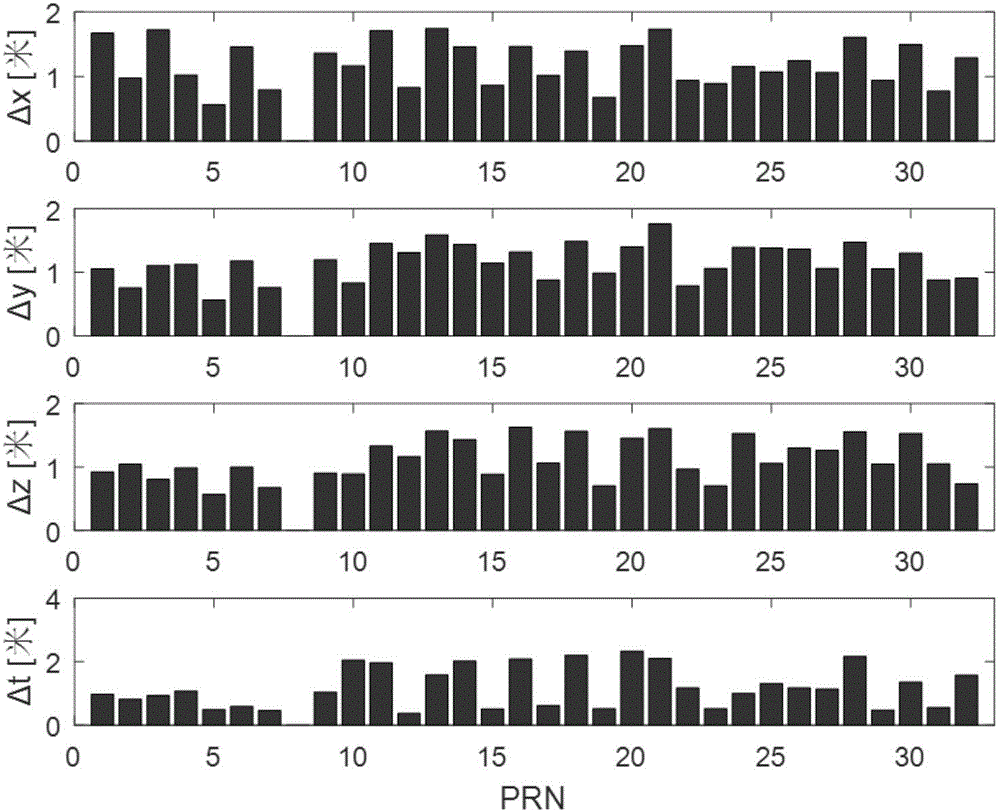
图2是本发明提供的星历星钟改正误差；

图3是本发明提供的星历星钟改正误差导致的用户测距误差；

图4是本发明提供的完好性参数对用户测距误差的包络情况；

图5是使用本发明的星历星钟改正参数和完好性参数的情况下的定位误差和保护级；

图6是使用本发明的星历星钟改正参数和完好性参数的情况下一类精密进近服务的可用率。

具体实施方式

下面将结合附图和实施例对本发明作进一步的详细说明。

本发明提出了一种应用于星基增强系统的星历星钟改正参数及空间信号完好性参数方法，该方法的核心思想是利用星历星钟预测值消除广播电文拟合误差，并利用实时观测量校正星历星钟预测误差。如图1所示，具体包括如下步骤：

步骤一：获取实时观测量，并计算伪距残差；

实时观测量包括GNSS的导航信号的载波观测量和码伪距观测量两种观测量，这两种观测量中均包含星历星钟误差、电离层延迟误差、对流层延迟误差、多径和接收机热噪声误差、接收机钟差误差等误差量，利用双频载波平滑码伪距、大气观测数据估计对流层延迟、站间时间同步等手段可以消除上述各个误差量的主要项，由此得到伪距残差Δρ₁，Δρ₁包含了星历星钟误差和观测残差：

Δρ₁＝Δx·l-ΔB+ε

其中，Δx和ΔB分别为星历误差和星钟误差，l为接收机指向卫星的单位矢量，ε为观测残差。

步骤二：计算星历星钟先验误差；

星历星钟先验误差定义为星历星钟预测值与星历星钟广播值之间的差值：

Λ＝cov(X_ap)＝cov(X_pred)

其中，X_ap为星历星钟先验误差，X_pred为星历星钟预测值，X_BE为通过GNSS广播电文计算得到的星历星钟广播值，Λ为星历星钟先验误差的协方差，cov(x)表示计算x的协方差。

步骤三：融合先验误差和实时伪距残差；

每颗卫星的先验误差和实时伪距残差的融合通过最小方差无偏估计器(MVUE)实现：

X_MV＝X_ap+ΛH^T(HΛH^T+R)^-1(Z-HX_ap)

P_MV＝Λ-ΛH^T(HΛH^T+R)^-1HΛ

其中，X_MV为MVUE输出的星历星钟误差估计值，实时观测矢量Z＝[Δρ_1,1 Δρ_1,2 … Δρ_1,n]^T，Δρ_1,i表示第i个监测站对该卫星的伪距残差Δρ₁，n为可以观测到该卫星的监测站总数，P_MV和R分别是X_MV和Z的协方差，地面监测站对卫星的观测矢量H的第i行为[l -1]。

步骤四：对步骤三的融合结果进行卡尔曼滤波，得到星历星钟误差估计值；

卡尔曼滤波器的关键参数如下：

1)状态方程为：

X_K(k)＝Φ_K(k)X_K(k-1)+v_K(k)

其中：k代表t_k时刻，X_K(k)表示状态矢量，Φ_K(k)表示状态转移矩阵，v_K(k)表示噪声矢量。

状态矢量X_K(k)包含12个参数：

其中，x、y、z和Δt分别代表ECI坐标系下的三维卫星位置和卫星相对于GNSS系统的时间差，和分别表示对x求时间的一阶导数和二阶导数。

状态转移矩阵Φ_K(k)为：

其中，w_k为卫星在轨道平面内运动的角速度，T为滤波间隔，α取为

噪声矢量v_K(k)的协方差矩阵为：

其中，S_x、S_y、S_z和S_Δt分别为三维位置和时钟的噪声功率谱密度。

2)k时刻的观测方程为：

Z_K(k)＝H_KX_K(k)+ε_K(k)

其中：Z_K(k)表示观测矢量，H_K(k)表示观测矩阵，ε_K(k)表示观测误差。

观测矢量Z_K(k)为ECI坐标系下的星历星钟状态估计值：

其中，是从ECEF坐标系到ECI坐标系的旋转矩阵。

观测矩阵H_K(k)是时不变矩阵：

ε_K(k)的协方差矩阵R_ε(k)为：

其中，P_MV(i,j)为P_MV矩阵中第i行第j列元素。

按照上述卡尔曼滤波器进行滤波，并由此得到ECEF坐标系下的星历星钟误差估计值X_esti为：

其中，和分别为ECI坐标系下的三维卫星位置和星钟误差，矢量中的四个元素依次是X_K的第1、4、7、10个元素。

步骤五：对星历星钟误差估计值进行拟合量化，从而得到星历星钟改正数广播值；

首先，汇总前N个时刻内基于同一组广播电文计算得到的星历星钟误差估计值集{X_esti}，N不超过900。

随后，利用最小二乘法拟合星历星钟改正数，具体如下：

其中，和依次为X_esti(k)的四个元素，t₀是星历星钟改正数的参考时间。

最后，将星历星钟改正数按照SBAS接口控制文档的要求进行量化，得到星历星钟改正数的广播值X_AK。

步骤六：计算使用星历星钟改正数广播值后的伪距残差；

使用X_AK后的伪距残差为：

Δρ₂＝Δρ₁+[l -1]X_AK

其中：Δρ₂表示使用X_AK后的伪距残差；

步骤七：利用步骤六得到的伪距残差计算星历星钟协方差；

取最近6秒(6秒为精密进近服务的告警时间门限)内的伪距残差集{Δρ₂}，由此星历星钟协方差P_SIS计算方法为：

其中，I为[-l 1]，P₀为ECEF坐标系下的星历星钟改正误差协方差，由ECI坐标系下的星历星钟改正误差协方差P_K的部分元素旋转得到，P_K(i,j)为卡尔曼滤波器后验协方差矩阵P_K中第i行第j列元素，s_min为取为星历星钟改正误差的历史样本的均方根值，mean({Δρ₂})和std({Δρ₂})分别表示计算{Δρ₂}的均值和标准差，为标准正态分布中1-P_HMI所对应的分位数，P_HMI为空间信号危险误导信息的概率，为系统设计值。

步骤八：分解步骤七得到的星历星钟协方差，并量化得到完好性参数广播值。

完好性参数包括两部分：一是随着星历星钟改正参数一起播发的协方差矩阵参数，另一部分是至少每6秒播发一次的参数，在单频SBAS中该参数为UDREI，在DFMC SBAS中该参数为DFREI，UDREI和DFREI参数表达范围是0～15。

完好性参数广播值量化策略为：当星历星钟改正参数更新时，遍历UDREI(或DFREI)，计算每个UDREI(或DFREI)数值对应的协方差矩阵参数，选择拟合误差最小的UDREI(或DFREI)数值及其对应的协方差矩阵参数作为空间信号完好性参数的广播值；当UDREI(或DFREI)更新时，根据协方差矩阵参数计算对应的UDREI(或DFREI)。

实施例：

利用本发明提供的方法，结合实测数据，详细说明本发明的星历星钟改正参数及空间信号完好性参数算法。

实施例1

将P_HMI设定为1×10^-5，则为4.42。所用的数据包括：GPS广播电文和精密星历、WAAS广播电文和WAAS监测站接收机天线相位中心的精确坐标、WAAS监测站的观测数据(观测频点为L1和L2，采样频率为1Hz)，以及IGS超快速星历。数据起止时间为2015年5月21日至6月19日，共30天，这段时间内GPS卫星处于正常状态，电离层也没有出现特别明显的异常活动。由于PRN 8未分配到一个健康的卫星信号，因此该卫星的统计数据是缺失的。

利用本发明提供的方法，可以获得星历星钟改正参数及其对应的空间信号完好性参数。分别通过星历星钟改正误差、完好性参数对URE的包络和定位性能三个角度对本发明的计算结果进行分析。

星历星钟改正参数的改正误差的均方根值如图2所示，从上至下依次为三维星历误差和星钟误差，由图2可知各颗卫星的星历误差在各个轴向上均小于2米，星钟误差小于3米。将星历星钟改正误差投影到用户方向即可得到URE，URE的均方根值如图3所示，可知各颗卫星的使用星历星钟改正参数后的URE分布在0.4米～1.4米。

为了方便描述空间信号完好性参数对使用星历星钟改正参数后的URE的包络，定义归一化的URE为：

其中，将NURE的概率密度曲线绘于图4，同时将标准正态分布的概率密度曲线绘于图4，可见本方法的|NURE|超过4.42的样本共有45个，超出样本数约占总样本数的5.42×10^-6，该数值小于P_HMI，满足完好性要求。

利用各个站点对GPS的观测数据进行定位解算，解算结果如图5所示，图5的上侧为95％的水平定位误差和垂向定位误差，图5的下侧为99.9％的水平保护级和垂向保护级。由图5可知，水平定位误差和垂向定位误差分别约为2米和3米，水平保护级和垂向保护级分别约为10米和18米。对于一类精密进近服务，其垂向保护级要求小于15米，将各个站点的垂向保护级小于15米的时间占比绘于图6，可见各个站点中一类精密进近服务可用率的最小值约为92.09％，最大值约为99.93％。

综上可知，本发明所提供的应用于星基增强系统的星历星钟改正参数及空间信号完好性参数算法具备较高的星历星钟改正精度、准确的空间信号完好性参数，能够仅依赖于GPS系统就基本提供一类精密进近服务。