草地植被参数获取方法与流程

本发明涉及无人机激光雷达(Lidar)数据处理
技术领域：
，具体涉及一种草地植被参数获取方法。
背景技术：
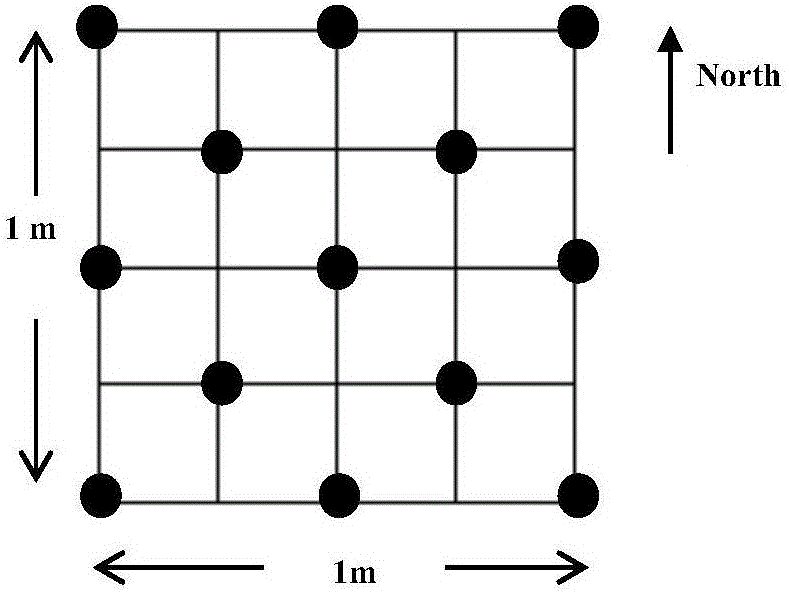
：草原占据我国半壁江山，是广大边疆牧区最主要的农业生产资源，也是我国最大的生态屏障和陆地碳汇。但自建国以来，我国退化草原面积已达90％以上，严重退化草原占50％。草原退化加之非生长季过度利用(尤其秋季打草、翻耕和冬季放牧)，导致草地生产力下降，更造成春季沙尘灾害频繁发生，给人类的生产与生活带来了严重灾难，也严重影响了生态环境建设和国民经济发展。因此及时准确地掌握非生长季草原上枯草残留的时空分布状况，对合理开发和利用非生长季的草地资源(如放牧等)，以免过度利用引起生产力下降、春季沙尘等灾害，进而保障牧民生活、边疆稳定和国家生态安全等具有重要的经济和社会意义。草地冠层高度、盖度和生物量是反映非生长季草原状况最直接的三个指标，其动态反演是草地生态遥感相关领域研究的热点问题。现有的研究多集中于生长季的草地生物量反演，所用方法多为基于卫星植被指数的方法。而非生长季的草地植被大都干枯，使得以往基于植被指数的生长季草地遥感监测技术失效，地面调查也更加困难，因而迫切需要发展不依赖植被指数的新的遥感理论和方法以支撑非生长季的草地参数提取和生物量反演。近年来，无人机Lidar技术以其成本低、操作简单、不依赖植被指数等优势，在森林生物量精准反演、环境监测等领域获得广泛应用。然而由于草地特征点不明显，地面样方较小(通常1×1m)，无人机定位定姿系统(positionandorientationsystem,POS)精度低，草地冠层高度较矮(通常仅10-50cm)，盖度高(草甸草原通常在60-80％以上)，基于无人机Lidar数据反演草地冠层高度、盖度和生物量的精度很难保证。其难点在于如何使地面样方数据与Lidar数据准确匹配，使地面样方与Lidar反演数据具有更高的相关性。现有的方法是根据全球定位系统(GPS)数据，直接将地面样方数据与Lidar数据对应。地面手持GPS数据的误差通常达5-10m，无人机POS数据误差也在1m左右，直接将地面样方与Lidar数据相对应，当草地异质性较大时会存在严重的误匹配现象。技术实现要素：针对现有技术中存在直接使用带误差的GPS数据将地面样方数据与Lidar数据对应来反演草原植被参数容易反演精度低的现象，本发明要解决的技术问题是提供一种使用GPS均方根误差提高Lidar反演草地植被参数精度的方法，根据地面和无人机的GPS精度(均方根误差)数据适时调整无人机Lidar数据的窗口大小，以提高地面样方与Lidar数据间的相关性，从而显著提高了基于无人机Lidar数据反演草地参数的精度。为了解决上述问题，本发明实施例提出了一种草地植被参数获取方法，包括：步骤1、根据无人机定位定姿POS系统数据，对获取的激光雷达点云数据进行地理编码处理，以为所述激光雷达的点赋地理坐标；步骤2、根据获取的激光雷达点云数据，将预设区域分为地面点、植被点、其他点；其中所述植被点为高于地表预设高度的点；步骤3、计算植被点到由地面点拟合的数字地表模型的距离，以获取植被的冠层高度和盖度；步骤4、构建地面实测数据与使用最佳激光雷达数据采样窗口Wd采样的冠层高度和盖度数据间的线性关系，以反演冠层高度、盖度和生物量。进一步的，所述步骤2具体包括：根据公式(1)计算采样窗口Wd内平均冠层高度，所述平均冠层高度为采样窗口Wd内的植被高度的平均值；MeanCH(i,j)＝mean[h(u,v)],u∈Wd(i,j)(1)其中，h(u,v)代表位置(u,v)的初始冠层高度；Wd为以(i,j)为中心、以d为边长的采样窗口；根据公式(2)计算采样窗口Wd内的最大冠层高度；其中最大冠层高度为采样窗口Wd内的植被冠层高度的最大值：MaxCH(i,j)＝max[h(u,v)],u,v∈Wd(i,j)(2)根据公式(3)计算植被冠层覆盖度，所述植被冠层覆盖度为植被点个数占全部点的比例：FVC(i,j)=Nh(u,v)≥2cmNall,u,v∈Wd(i,j)---(3)]]>其中Nh(u,v)≥2cm为高于地面2cm的植被点个数，Nall为全部点个数。进一步的，所述步骤2中的采样窗口Wd的边长d通过以下方法确定：确定预设的边长d取值范围，以及调整步长δd，然后通过以下公式(4)计算出地面样方值与Lidar提取值间的决定系数R2趋于稳定不变时的值作为边长d|R2(dk+1)-R2(dk)|→0,k=1,2,4,...,50dk=k×δd,δd=0.2---(4)]]>其中，d为第k个采样窗口边长取值。进一步的，所述步骤4具体包括：根据公式(5)计算平均冠层高度反演值，所述平均冠层高度反演值为采样窗口内的冠层高度平均值的a倍：MeanCH′(i,j)＝a×MeanCH[h(u,v)],(u,v)∈Wd(i,j)(5)根据公式(6)计算盖度，所述盖度为采样窗口Wd内的植被点占全部点的比例与a的乘积：FVC′(i,j)＝a×FVC[h(u,v)],(u,v)∈Wd(i,j)(6)最大植被观测高度反演值为采样窗口Wd内的最大植被冠层高度的a倍：MaxCH′(i,j)＝a×MaxCH[h(u,v)],(u,v)∈Wd(i,j)(7)生物量由以下公式计算：＝a×MeanCH；＝a×MaxCH；＝a×FVC；＝a×MeanCH+b×MaxCH；Biomass＝a×MeanCH×MaxCH；＝a×MaxCH+b×FVC；＝a×MaxCH×FVC；＝a×MeanCH+b×FVC；＝a×MeanCH×FVC。本发明的上述技术方案的有益效果如下：1、本发明实施例可以借助地面和无人机的GPS精度(均方根误差)数据显著提高基于无人机Lidar数据反演草地参数的精度。实验表明，与不根据GPS精度(均方根误差)数据调整Lidar数据采样窗口相比，地面测量草层高与Lidar提取草层高的决定系数R2能提高0.012(1.3％)，RMSE能降低0.487cm(6.6％)。2、本发明实施例提出使用GPS均方根误差提高Lidar反演草地植被参数精度的方法，能够准确区分出6个放牧梯度，表明提出的方法有极高的精度，在样区(每个样区约200m×300m)级别上能够区分出1-2cm的草地冠层高度差别，3％的盖度差别，15g·m-2生物量差别，而不根据GPS精度(均方根误差)数据调整Lidar数据采样窗口，仅能区分其中冠层高度差别最大的4个放牧梯度(0、1、2、3)，对于区分差别较小的4、5放牧梯度无能为力。3、本发明实施例表明在有条件的情况下，应采用更高精度的手持GPS设备，如采用实时差分(RTK)GPS。与使用手持GPS相比，采用RTKGPS，地面测量草层高与Lidar提取草层高的决定系数R2能提高0.045(5.61％)，RMSE能降低1.11cm(11.84％)。该发明特别适合对冠层高度较低、特征不明显、高精度GPS难以普及的广大草原地区的草地冠层高度、盖度和生物量反演。附图说明图1为本发明实施例的使用GPS均方根误差提高Lidar反演草地冠层高度、盖度、生物量精度的流程示意图；图2为本发明实施例的草地冠层高度、盖度地面测量方案示意图；其中25个网格交叉点代表盖度测量点位；13个黑点表示冠层高度采样点位。图3a和图3b为本发明建议的Lidar数据采样窗口决定示意图；当地面样方的定位精度(RMSE)低于Lidar数据的定位精度时，采用图3a所示的采样窗口；当地面样方的RMSE高于Lidar数据的定位精度，采用(b)所示的采样窗口。具体实施方式为使本发明要解决的技术问题、技术方案和优点更加清楚，下面将结合附图及具体实施例进行详细描述。本发明提供一种使用GPS均方根误差提高无人机Lidar反演草地植被参数精度的方法，根据地面和无人机的GPS均方根误差数据确定的最佳无人机Lidar数据的采样窗口Wd，并将其应用于冠层高度、盖度和生物量估算的步骤如下：步骤1、根据无人机定位定姿系统(POS)的数据，对原始无人机Lidar点云数据进行地理编码处理，为每个无人机Lidar点赋地理坐标，坐标格式为UTM投影坐标系(即XYZ格式)以便于计算植被冠层高度，确定无人机Lidar数据采样窗口。步骤2、根据点云数据计算的坡度、独立点到地表模型的角度等对地理编码处理后的点云数据进行监督分类，将其分为地面点、植被点(高于地表2cm的点)和其他点。步骤3、计算植被点到由地面点拟合的数字地表模型(DSM)的距离，提取植被的冠层高度和盖度。其中，平均冠层高度为采样窗口内植被冠层高度的平均值：MeanCH(i,j)＝mean[h(u,v)],u∈Wd(i,j)(1)式中，h(u,v)代表位置(u,v)的初始冠层高度；Wd为以(i,j)为中心、以d为边长的采样窗口；其中，最大冠层高度为采样窗口内植被冠层高度的最大值：MaxCH(i,j)＝max[h(u,v)],u,v∈Wd(i,j)(2)植被冠层覆盖度定义为植被点个数占全部点的比例：FVC(i,j)=Nh(u,v)≥2cmNall,u,v∈Wd(i,j)---(3)]]>式中，Nh(u,v)≥2cm为高于地面2cm的植被点个数，Nall为全部点个数。上述步骤中，最关键的是根据地面样方数据与无人机Lidar提取参数间的决定系数R2，计算最适宜的无人机Lidar数据采样窗口边长d。由于无人机Lidar通常具有很高的定位精度(定位精度通常<1m)，因此本发明实时例中，采样窗口边长d取值范围是根据采集地面样方坐标的GPS来确定。在本发明的一个实施例中，采用Garmin公司的手持GPS的定位精度为2.6m，UniStrong公司的RTK的定位精度为0.97m。为了充分调查采样窗口d与定位精度间的关系，将采样窗口d的取值范围定义为0-10m，间隔为0.2m。采样窗口边长d定义为当地面样方值与无人机Lidar提取值间的决定系数R2趋于稳定不变时的窗口边长值，即|R2(dk+1)-R2(dk)|→0,k=1,2,4,...,50dk=k×δd,δd=0.2---(4)]]>其中，d为第k个采样窗口边长取值。如何确定最佳的无人机Lidar数据采样窗口边长d是本发明得以应用的关键。在本发明实施例中，取地面样方值与无人机Lidar提取值间的决定系数R2趋于最高且稳定不变时的窗口边长值作为最恰当的无人机Lidar数据采样窗口d。图3a和图3b为本发明实施例的无人机Lidar数据采样窗口决定示意图。依据为：不考虑物种、植被冠层异质性等对相关性的影响，地面样方值与无人机Lidar采样矩阵的地理位置完全对应时，地面样方值与无人机Lidar提取值间的相关最好，决定系数R2在理论上达到最大值。然而，由于GPS误差的存在，且草地的特征点不明显，让地面样方值与无人机Lidar采样矩阵的地理位置完全对应是几乎不可能的。增加地面样方或无人机Lidar采样窗口大小在一定程度上能提高地面样方值与无人机Lidar提取值的相关性，但由于地面样方通常较小(一般不超过1×1m2)，通过增加地面样方大小提高相关性需增加额外成本。因此本发明通过无人机Lidar采样窗口来提高地面样方值与无人机Lidar提取值的相关性，进而提高无人机Lidar反演草地植被参数精度。同时，由于决定系数R2存在一定偶然性，单看某个采样窗口值对应的决定系数R2并不能保证地面样方值与无人机Lidar提取值间的地理位置对应最好。而当决定系数R2趋于最高且稳定不变时，地面样方值与无人机Lidar提取值间的相关性最好且稳定，理论上地理位置也对应最好，这时使用地面样方值校准无人机Lidar提取值的准确性最高。本发明实施例中，采用采样窗口d为两倍的地面样方值和无人机Lidar数据的较大的RMSE(地面样方的定位精度)，即当地面GPS的RMSE大于无人机Lidar数据定位精度时，d为两倍的地面GPS的RMSE，而当Lidar数据定位精度的RMSE大于地面GPS的RMSE时，d为两倍的Lidar数据定位的RMSE。该方法能够让地面样方值与Lidar提取值间的相关性达到最高且稳定的逻辑基础是：无论采用手持GPS还是RTK，该Lidar采样窗口都有约87％(假如误差服从标准正态分布)概率能覆盖样方的地理位置。步骤4、构建地面实测数据与使用最佳Lidar数据采样窗口d采样的冠层高度和盖度数据间的线性关系，反演冠层高度、盖度和生物量。本发明实施例主要目的之一是分析Lidar数据采样窗口大小对地面测量值与Lidar提取值间相关性的影响。为了简化计算量，本发明实施例仅使用不带截距的线性关系拟合地面测量值与Lidar提取值间的关系。平均冠层高度反演值定义为采样窗口内的冠层高度平均值的a倍：MeanCH′(i,j)＝a×MeanCH[h(u,v)],(u,v)∈Wd(i,j)(5)盖度为采样窗口内的植被点占全部点的比例与a的乘积：FVC′(i,j)＝a×FVC[h(u,v)],(u,v)∈Wd(i,j)(6)最大植被观测高度反演值为采样窗口内的最大植被冠层高度的a倍：MaxCH′(i,j)＝a×MaxCH[h(u,v)],(u,v)∈Wd(i,j)(7)生物量反演值采用表1所示的公式：表1生物量反演公式以下根据一个具体的例子对本发明实施例进行进一步说明。本例子是利用一组无人机Lidar数据及对应的两组地面样方数据对前述本发明实施例提出的“使用GPS均方根误差提高无人机Lidar反演草地植被参数精度的方法”的效果进行了测试，并与其他不使用GPS均方根误差的Lidar反演方法进行了对比。本例子中，模型评估方案设计在内蒙古呼伦贝尔草原站的肉牛放牧平台。该放牧平台有6个放牧梯度，每个放牧梯度有3个重复。W/M/E0-5代表每个小区分别放养0、2、3、4、6、8头200-300kg的标准牛，因而每个小区内的草地冠层高度、盖度、生物量都明显不同。无人机平台采用八旋翼无人机，Lidar传感器采用Velodyne公司的HDL-32E传感器，飞行参数见表2。表2传感器及数据获取参数地面草地冠层高度和盖度测量方案见图3。地面样方的坐标采用Garmin公司的手持GPS(定位精度为2.6m)和UniStrong公司的RTK(定位精度为0.97m)测得。第一组地面样方包括20个，其中心点坐标由手持GPS和RTK同时测得。第二组地面样方包括90个，其中心点坐标仅有手持GPS测得。分析Lidar数据采样窗口大小d对地面测量值与Lidar提取值间的相关性R2和均方根误差RMSE的影响发现：(1)Lidar数据采样窗口大小对R2和RMSE均有很大影响。通常最初R2随着d增加而增加，RMSE随着d增加而降低增加。当d增加到一定值后，R2和RMSE达到最大且稳定不变，随后缓慢下降。(2)无论使用手持GPS，还是使用RTK，亦或同时使用手持GPS和RTK，除地面测量的最大冠层高度与Lidar提取的最大冠层高度间的R2和RMSE外，其余参数的地面测量值与Lidar提取值间的R2均在两倍的地面GPS(包括手持GPS或RTK)的RMSE附近，即对于使用手持GPS测量样方坐标的一组数据，当d＝2×2.6＝5.2m时，或对于使用RTK测量样方坐标的一组数据，当d＝2×0.97≈2m时，达到了最大且稳定不变，RMSE达到了最小且稳定不变。接下来，使用了6个放牧梯度和地面测量值两种方法对提出的草层高、盖度和生物量反演模型进行了评估。首先，统计每个放牧梯度内冠层高度、盖度和生物量，然后将所每个放牧梯度内的统计值与放牧梯度对比，看提出的方法是否能区分每个放牧梯度。对比结果表明，本发明实施例所提出使用GPS均方根误差提高Lidar反演草地植被参数精度的方法，能够准确区分出6个放牧梯度，表明提出的方法有极高的精度，在样区级别上能够区分出1-2cm的草地冠层高度差别，3％的盖度差别和15g·m-2生物量差别。而采用不根据GPS精度(均方根误差)数据调整Lidar数据采样窗口的方法，仅能区分其中冠层高度差别最大的4个放牧梯度(0、1、2、3)，对于区分差别较小的4、5放牧梯度无能为力。此外，对比表1所示的所有模型发现平均高度是所有单变量模型中预测生物量最好的模型，可以解释78.3％的变量，RMSE为109.1g·m-2(占最大生物量的18.7％)；组合使用高度和盖度并不能显著提高生物量反演精度，可以解释78.4％的变量，RMSE为108.9g·m-2(占最大生物量的18.6％)，原因是研究区域较小，高度和盖度呈现高度相关(相关系数r达0.898)，但与采用分段函数拟合每个放牧梯度的生物量的方法相比，能显著平衡两个仅使用高度和盖度的单变量模型在每个放牧梯度段拟合生物量的残差，如下表3所示。表3单变量模型与组合模型对比以上所述是本发明的优选实施方式，应当指出，对于本
技术领域：
的普通技术人员来说，在不脱离本发明所述原理的前提下，还可以作出若干改进和润饰，这些改进和润饰也应视为本发明的保护范围。当前第1页1 2 3