X射线线阵探测器校正与滤波的制作方法

本发明涉及一种X射线线阵探测器校正与滤波方法，该方法提出了使用改进的两点校正算法进行校正，半隐式差分格式的偏微分方程算法滤波，属于图像处理和信号处理领域，可应用于X射线检测产品时对图像进行校正与滤波。

背景技术：

作为无损检测技术的一种，X射线检测技术是现代物理学、电子学、计算机科学等多学科综合应用的产物，正以其优越的性能和特有的检测方式被广泛应用于零部件检测、轮胎检测、食品检测、安全检测等诸多领域，尤其适用于高速在线检测的要求。对X射线图像进行校正与滤波是至关重要的，可提高检测的质量。

目前，主要的校正处理方法有插值法和逼近法。分段插值算法虽然校正精度较高，但存在分段数量选择困难，分段过多运算量相应增加，分段过少会导致精度下降。基于响应曲线的三点分段算法，虽然能很好地逼近响应曲线，但需事先确定响应曲线的两个拐点，若拐点判别错误，整体的校正结果会出现偏差，相对较复杂。根据噪声的特点和产生原因，可分为3类：本底噪声、随机噪声、孤立噪声。主要的滤波方法为差值法消除本底噪声、卡尔曼滤波法滤除随机噪声、中值滤波法消除孤立噪声，但是需要进行多种滤波，较为复杂，抑制噪声的效果并不理想，数据波动依然较大。

针对以上问题，提出了改进的X射线图像校正与滤波模型。提出了采用两点校正求感光元件的补偿偏置量因子和补偿增益因子，使用半隐式差分格式的偏微分方程处理算法去噪。最后给出实验结果，证明该方法可以有效地解决X射线线阵探测器存在的由于像素响应不均和噪声所造成的图像质量下降问题。

技术实现要素：

本发明的目的是克服现有技术的上述不足，提出了一种X射线线阵探测器校正与滤波方法，该方法能够准确有效地校正图像，还能抑制噪声的影响。为此，本发明采用如下的技术方案：

1.利用X射线线阵探测器采集数据；

2.建立两点校正模型；

3.建立求解补偿增益因子和补偿偏置因子模型；

4.半隐式差分格式的建立；

5.对半隐式偏微分方程进行迭代求解；

本发明具有如下的技术效果：

1.方法简单，易于实施。本发明利用改进的两点校正算法，相对于其他算法而言，效率更高。

2.准确性高。本发明在滤波过程中，采用半隐式差分格式的偏微分方程算法，实验证明提高了检测精度。

3.对于X射线检测相关领域均适用，提高检测质量。

附图说明

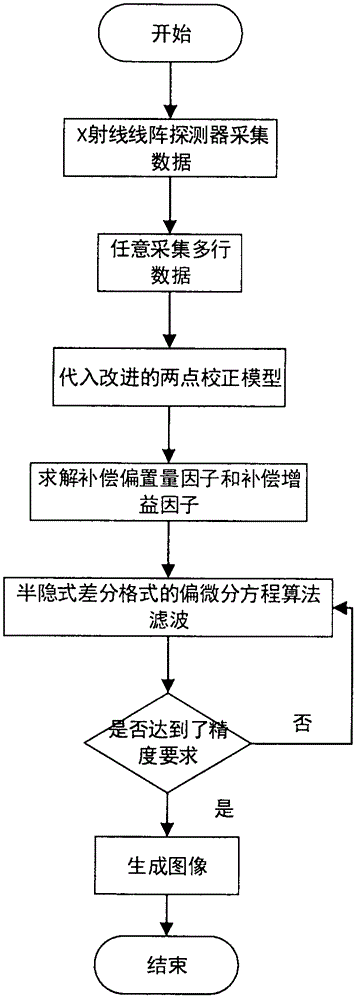
图1：本发明总体方案流程图。

图2：探测器的内部结构示意图。

图3：X射线检测装置系统结构示意图。

图4：未校正滤波的数据，图(a)为理想状态下无X射线行数据，图(b)为实际情况下行扫描数据，大小为1×9216。

图5：未校正且有噪声的X射线图像。

图6：四邻点集合。

图7：经过两点校正后的X射线图像。

图8：不同滤波法处理结果的平均均方误差比较。分别为均值滤波、卡尔曼滤波、本文的方法。

图9：不同滤波方法处理的结果图。图(a)为均值滤波、图(b)为卡尔曼滤波、图(c)为本文的方法。

图10：经过该模型校正、滤波后的完整图像。

具体实施方式

本发明的流程图如图1所示，首先使用X射线线阵探测器采集数据，然后建立补偿偏置因子和补偿增益因子的模型，将两行数据带入，求解补偿因子，对所有数据进行校正。建立半隐式差分格式的偏微分方程模型，输入图像数据进行迭代，滤出本底噪声、孤立噪声、随机噪声。下面结合附图，对本发明技术方案的具体实施过程加以说明。

1.X射线线阵探测器采集数据

当X射线穿透被测工件到达X射线线阵探测器后，就携带了物体内部的信息，X射线线阵探测器的感光元件是按行排列的，对携带了物体内部信息的X光信号采用逐行扫描的方式对其接收，并经过转换器转换为电信号，该信号在标准化后经过以太网传输到计算机上，计算机将这些行数据按顺序重新排列成整幅图像。为了完整地得到图像，需要使被测工件通过X射线成像区域的速度与X射线线阵探测器的积分时间相一致，即传送带的速度V与X射线线阵探测器的扫描速度相匹配，应符合公式：

式中：V为传送带移动速度，D为像素间隔，N为像素合并个数，T为积分时间，M 为放大倍数。由于X射线线阵探测器的接收区域为一条狭长的细缝，需要调整角度和位置，使X射线光源、被测物体及X射线线阵探测器的接收区域在一条直线上，即可得到较完整的图像。

2.建立X射线线阵探测器两点校正的模型

研究表明，在一定程度范围内，当X射线发射后，X射线线阵探测器内的感光器件对X射线的响应变化率可以近似地看作是线性变化。由于每个感光元件的偏置量和增益不同，造成对于接收同样大小能量的像素，其响应输出量不同，因此，对于X射线图像校正的实质就是对像素点的响应率偏置因子和增益因子进行修正。

假设每个X射线感光元件的响应满足公式：

上式中：Y_i表示第i个X射线感光元件的输出信号，K_i表示第i个感光元件的增益因子，表示第i个感光元件接收到的X射线的光能量，B_i表示第i个感光元件的偏置因子，N表示X射线线阵探测器的感光元件个数。

两点校正的目的是使每个感光元件在接收到相同大小X射线能量的时候，也输出一样大小的输出信号，输出满足：

式中：表示经过两点校正后的输出信号，Z_i表示增益校正因子，P_i表示偏置校正因子。经过两点校正后，满足：

由上式可知，若想使得感光元件的输出得以校正，每个感光元件只需代入两次不同大小的X射线能量，即每个点代入两次不同的值。既可以对感光元件响应的偏置量因子做补偿，也可以对增益因子做补偿。

3.求解两点校正的补偿偏置量因子和补偿增益量因子

选择两个定标点和为关闭X射线光源时接收的能量，为不放被测工件的情况下打开X射线光源时接收的能量，选择电压＝80kV，电流＝0.3mA即：具体步骤如下：

第一步，关闭X射线光源，即在条件下连续采集M行数据，求出该样本下感光元件的输出信号样本均值，即：

式中：表示在接收X射线能量为时第i个感光元件在样本容量为M下求取的输出信号的均值。表示在接收X射线能量为时第i个感光元件在样本容量为M下第j次的输出信号。

第二步，打开X射线光源，在条件下连续采集M行数据，求出该样本下感光元件的输出信号样本均值，即：

式中：表示在接收X射线能量为时第i个感光元件在样本容量为M下求取的输出信号的均值。表示在接收X射线能量为时第i个感光元件在样本容量为M下第j次的输出信号。

第三步，将所有感光元件的平均输出信号的期望作为目标输出信号，即：

令代入：

解此方程组可得：

推导出每个感光元件的偏置量因子和增益因子：

推导出了每个感光元件进行校正时所需的补偿偏置量因子和补偿增益因子。当开始正 常工作时，X射线线阵探测器每扫描输出一行数据后，求出补偿因子即可进行校正。

4.偏微分方程的半隐式差分法

设I：R²→R代表一幅灰度图像，其中I(x，y)是像素点(x，y)处的灰度值。引入时间参数t，则图像演化过程可以表示如下：

其中表示图像u对时间t的一阶导数，F表示针对不同的图像处理过程所给出的偏微分算子，原始图像I可看作初始条件。这样，此微分方程的解u(x，y，t)就是在时间参数t下处理后的图像，这就是偏微分方程的思想。

由于热传导方程各向同性线性扩散所产生的缺点，即会使图像边缘模糊，为了达到去噪同时保护图像边缘信息的目的，Perona和Malik提出P-M方程：

其中，div是散度算子，是梯度算子，I(x，y)为原始图像，是一个平滑的非增函数，称为扩散系数。

由于P-M方程所得到的图像平滑是有条件的，在有些情况下，方程的解是不稳定的。为此，对P-M方程正则化：

其中，G_σ表示方差为σ的高斯函数。此方程保证了非线性扩散是稳定的，存在唯一的连续依赖于初值I(x，y)的解。

半隐式差分格式所得到的方程组是线性的，这就使得数值计算比非线性方程组简单了许多，并且也是绝对稳定的。采用由Weickert等提出的半隐式方案：

其中，p₁ p₂ p₃ p₄是s的四邻点，Γ_s表示以s为中心的四邻点集合。

g的代数表达式即边缘函数采用下面的形式：

其中，k是可调参数，又称反差参数，可以控制g随r变化速度的快慢。具体半隐式格式表示如下：

式中，τ表示时间步长，g采用“半点”离散格式，即用在n层数据两个相邻整点值来求平均值，得到的结果来近似它在“半点”上的值，表达如下：

用矩阵形式表示如下：

进一步推导：

式中uⁿ⁺¹和uⁿ表示在n+1和n时刻的图像矢量，是M×N维列矢量；Aⁿ表示MN×MN维矩阵，I表示MN×MN维单位矩阵。矩阵Aⁿ的元素为

5.对半隐式偏微分方程进行迭代求解

将一次迭代分为两个子步骤，首先对uⁿ的行和列各作一维扩散，得到两个中间结果 和即

然后对和求平均值完成一次完整的迭代。即

进一步推导得：

完成uⁿ后，作如下操作：

第一步，首先令

第二步，然后计算f_σ＝f*G_σ，

第三步，对i＝1，…，M

(a)计算的三个对角线上的元素：

(b)一般采用Thomas算法求解得到

第四步，对于j＝1，…，N，

(a)计算的三个对角线元素；

(b)一般采用Thomas算法求解得到

第五步，计算

这就完成了一次完整的迭代。

本发明提出了一种X射线线阵探测器校正与滤波的方法，该方法提出将改进的两点校正算法和半隐式差分格式的偏微分方程处理方法想结合，快速校正数据，同时能有效滤除本底噪声、随机噪声、孤立噪声。相对于传统校正算法且忽略噪声影响的模型，处理后的数据的均方误差更小，提高了X射线检测质量。