一种基于傅里叶基函数的雷达目标识别方法与流程

本发明涉及微波遥感领域，特别是一种基于傅里叶基函数的雷达目标识别方法。

背景技术：

目前雷达目标识别方法一般包含以下几种：1、基于目标回波起伏的目标识别方法，该方法将雷达目标可看作多个散射体构成的复杂目标，各个散射体的雷达回波相互干涉，根据雷达目标回波的幅度与相位随着目标相对于雷达姿态不同，判断目标的形状与运动情况。该方法的缺点在于当近距离探测雷达目标时，由于目标的姿态的变化，会导致雷达目标散射截面积剧烈变化，造成距离测量的不稳定。2、基于高分辨雷达成像的目标识别方法，采用合成孔径雷达(SAR)或逆合成孔径雷达(ISAR)技术，可获取目标的形状信息。该方法的缺点在于当目标与雷达距离不能满足远大于目标尺寸时，需补偿和校正雷达距离和多普勒参数，带来了算法的复杂性和不确定性。3、基于状态空间法和矩形基函数的波形综合识别技术，采用状态空间法提取极点和矩形基函数构造E脉冲波形实现目标的特性识别，该方法在一定程度上揭示了E脉冲识别目标的可行性。该方法的缺点在于波形构造复杂，易受噪声影响，运算量大等问题。

王党卫、马兴义等在2006年12月第28卷第12期电子与信息学报上发表的论文“一种基于傅里叶级数的E脉冲识别波形综合方法”中提出一种用于傅里叶级数的E脉冲目标识别方法，但该方法只是基于相关参数的确定原则和波形合成框图，并未涉及极点快速提取和利用傅里叶基函数构造发射波形的方法，同时该论文仅采用简单的细体导线作为验证样本，并未涉及空中动目标检测等相关内容。

技术实现要素：

本发明解决的技术问题是：克服现有技术的不足，提供了一种基于傅里叶基函数的雷达目标识别方法。解决了空中动目标识别速度慢和识别概率低问题，通过目标时域电磁回波构造基于傅里叶基函数的E脉冲波形，完成雷达目标检测与识别。

本发明的技术解决方案是：一种基于傅里叶基函数的雷达目标识别方法，包括如下步骤：

(1)对雷达检测到的目标进行米波频段电磁仿真得到目标的N路时域散射波形，通过时域积分方程对目标的N路时域散射回波进行积分处理得到目标散射场的后时响应模型，其中，目标散射场后时响应模型包括雷达目标极点、雷达目标幅度、雷达目标相位，目标散射场后时响应开始的时间r(t)为

式中，a_n为目标的第n路时域散射波形的留数，σ_n为第n个目标时域散射波形的衰减因子，ω_n为第n路目标时域散射波形的衰减频率，为第n个目标时域散射波形的相位，n＝1，2，3，…，N；

进而得到目标散射场后时响应开始的时间r(t)的幅度衰减系数exp；

(2将步骤(1)得到的目标的N路时域散射波形发射至当前雷达检测到的目标，然后检测目标反射的N路时域回波，利用矩阵束法对得到的时域回波进行快速极点提取，得到第n路时域散射波形对应的时域回波的主极点s_n、复留数R_n、衰减因子σ_n、衰减频率ω_n，进而计算得到修正后的时域散射波形y(t)为

对修正后的时域散射波形y(t)进行采样，得到时域散射波形y(iT_s)为

式中，i为采样次数，T_s为采样间隔；

(3)构建傅里叶余弦基函数f_m(t)为

其中，m＝1，2，3，…，M，M为时域散射波形y(iT_s)极点个数，M＝2N，T_e为时域散射波形y(iT_s)的脉冲长度；

进而得到E脉冲波形e(t)为

然后对E脉冲波形e(t)进行矩阵化分解得到

M_2i,j为第i个时域散射波形y(iT_s)中第j个极点系数，M_2i-1,j为第i个时域散射波形y(iT_s)中第j个极点系数，i＝1，2，3，…，N，j＝1，2，3，…，2N；

根据E脉冲波形e(t)矩阵化分解得到的矩阵对应的行列式为零，计算得到α_m；

(4)重复步骤(1)-步骤(3)直至得到所有目标的E脉冲波形e(t)并存储；

(5)当进行目标识别时，将存储的一个目标的E脉冲波形e(t)对应的时域散射波形发射至待识别目标，然后将待检测目标的时域回波与当前目标的E脉冲波形e(t)进行卷积，如果卷积结果为0，则待检测目标类型与当前目标的类型一致，否则遍历存储的所有目标的E脉冲波形e(t)直至得到当前待检测目标的类型。

所述的采样间隔T_s＝0.5ns。

所述的步骤(3)中根据E脉冲波形e(t)矩阵化分解得到的矩阵对应的行列式为零，计算得到α_m的方法为线性最优法和最优边界约束条件法。

本发明与现有技术相比的优点在于：

(1)本发明方法与现有技术相比，通过米波频段电磁仿真，解决了对隐身飞行目标探测和识别问题，实现了利用宽频谱波形激励探测目标谐振，从而识别目标的效果；

(2)本发明与现有技术相比，通过矩阵束法对得到的时域回波进行快速极点提取，解决了克服了状态空间法缺陷，具有极点提取效率高和运算量小的优点；

(3)本发明与现有技术相比，通过傅里叶基函数构造方法，解决了矩形基函数构造法缺陷，具有抗噪声能力强、波形简单和识别效率高的优点。

附图说明

图1为本发明方法的流程图；

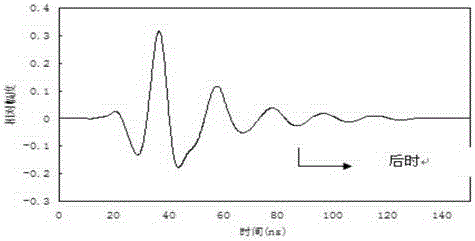
图2为本发明实施例中未采用本发明方法的E脉冲波形与其时域回波卷积结果示意图；

图3为本发明实施例中采用本发明方法E脉冲波形与其时域回波卷积结果示意图。

具体实施方式

如图1所示，为本发明方法的流程框图，主要步骤如下：

(1)对特定雷达目标进行米波频段电磁仿真，通过时域积分方程对目标时域散射回波进行积分处理得到目标散射场的后时响应模型，其中包括目标极点、目标幅度和相位，目标后时响应开始的时间；

式中，exp为r(t)幅度衰减系数，a_n为第n个时域散射波形的留数，s_n＝σ_n+jω_n为第n个时域散射波形的极点，σ_n为第n个时域散射波形的衰减因子，ω_n为第n个时域散射波形的衰减频率，为第n个时域散射波形的相位，T_l为目标后时响应的起始时刻，n＝1，2，3，…，2N；所述的雷达目标极点包括N对共轭的雷达目标极点；

(2)根据步骤(1)的结果，将时域散射波形反射至雷达检测到的目标，当检测到目标反射的时域回波，利用矩阵束法对得到的时域回波进行快速极点提取，即得到第i个目标反射时域波形主极点s_i，用于估计波形与原雷达回波进行对比；

式中，y(t)为目标反射时域波形，R_i第i个目标反射时域波形极点的复留数，s_i＝σ_i+jω_i为第i个目标反射时域波形的目标极点，σ_i和ω_i分别为目标反射时域波形的衰减因子和衰减频率，实际所得到数据是瞬态相应的离散情况，假设经过采样后的瞬态响应的后时部分可表示为：

式中，i＝1,2,3,…,M，M为时域回波共轭极点的个数，T_s为采样间隔，采样采样间隔T_s＝0.5ns。

现在定义两个矩阵：

式中，L为矩阵束参数，L＝1,2,3,…M，它的取值会影响到结果的精度，通过施密特分解可以将上面两个矩阵分解为：

[Y₁]＝[Z₁][R][Z₂]

[Y₂]＝[Z₁][R][Z₀][Z₂]

其中：

[Z₀]＝diag[Z₁,Z₂,...,Z_M]

[R]＝diag[R₁,R₂,...,R_M]

diag[·]表示大小为M×M的对角线矩阵。

现在考虑下面的矩阵：

[Y₂]-λ[Y₁]＝[Z₁][R]([Z₀]-λ[I])Z₂

式中，[I]是大小为M×M的单位矩阵。

显然，如果λ＝Z_i，i＝1,2,3,…,M,([Z₀]-λ[I])的第i行为零，因此Z_i是矩阵{[Y₂]；[Y₁]}的广义本征值。所以求解Z_i即求解形如下式的特征值问题：

{[Y₁⁺][Y₂]-λ[I]}

式中，[Y₁⁺]是[Y₁]的伪逆，可以表示如下：

[Y₁⁺]＝([Y₁]^H[Y₁])^-1[Y₁]^H

得到Z_i后，目标反射时域波形极点的复留数R_i可通过最小二乘法求解下式的问题：

(3)根据步骤(2)的结果，采用傅里叶余弦基函数方法对目标反射时域波形主极点所对应的留数R_i进行展开，构造E脉冲函数构造并设计发射波形，得到E脉冲波形各项参数。

傅里叶余弦基函数形式如下式

其中，f_m(t)定义为E脉冲的傅里叶余弦基函数，m＝1，2，3，…，M，M为时域散射波形极点个数，T_e为时域散射波形的脉冲长度。

通过上式得出E脉冲的函数表达式：

其中，M为时域散射波形极点个数，α_m为未知系数，T_e为时域散射波形的脉冲长度。

由上式得到E脉冲函数的傅里叶变换式为：

令可得

经过化简推导后，上式可以简化为：

将上式代入E脉冲的条件函数得到E脉冲相应的矩阵方程，求解即可得到起未知系数。以E脉冲为例详细讨论未知系数的求解过程。取M＝2N，并根据1≤n≤N可得：

其中：

通过施密特变换，上式M_n,m矩阵的形式可表示为：

其中，M_2i,j为第i个时域散射波形y(iT_s)中第j个极点系数，M_2i-1,j为第i个时域散射波形y(iT_s)中第j个极点系数，i＝1，2，3，…，N，j＝1，2，3，…，2N；

当存在非零解得条件是其行列式为零，即非满秩行列式，根据行列式为零可以得到脉冲长度T_e的精确取值，利用线性最优法和最优边界约束条件法，通过求解上式方程组即可得到E脉冲波形的未知系数α_m。

(4)根据步骤(1)的目标时域散射波形中的极点及其对应留数，构造相应的E脉冲时域波形，并将在计算中存储各个目标对应的E脉冲波形，把待识别目标的时域回波接收后也存储到计算机。

(5)根据步骤(4)通过采用傅里叶余弦基函数、矩形基函数构造的E脉冲波形函数与特定目标自身电磁散射时域回波卷积结果进行对比，如果卷积结果表现为零，则E脉冲波形与目标回波的卷积结果消除了目标的所有频率分量，即成功识别，如果卷积结果表现不为零，则表明卷积结果中包含其它频率分量，即未成功识别。

实施例

为了更清楚的表明本方法的优点，在此进行数学仿真，仿真条件：F15SE缩比模型，缩放尺寸是4.30m×2.89m×1.25m，入射方位角为30度，俯仰角为0度。

图2为未采用傅里叶余弦基函数构造E脉冲波形与时域回波卷积仿真结果，图3为采用本发明方法的卷积仿真结果图。从图中可以看出，未采用傅里叶余弦基函数的卷积为0的时刻为145ns，相对幅度为0.05，采用傅里叶余弦基函数的卷积0的时刻为130ns，相对幅度为0.3，因此采用本发明方法对特定目标时域回波构造E脉冲发射波形，可以缩短10～15ns识别时间，检测幅度提高6～7dB，验证本发明方法的有效性。

本发明说明书中未作详细描述的内容属本领域技术人员的公知技术。