沉积物水平延伸距离计算方法与流程

本发明涉及地质勘探领域，尤其是涉及一种沉积物水平延伸距离计算方法。

背景技术：

古代湖泊或者大海的边缘(湖岸、海岸)位置由于有河流的注入，会有大量的泥沙搬运至此，并沉积下来。经过数百万年的埋藏压实，古代沉积的泥沙发生成岩作用，形成一种内部发育有很多孔隙的储层岩石。该种岩石能够储藏丰富的油气资源，而且在古湖泊边缘广泛发育，成为我国东部油气勘探领域的一类重要的储油层。但是，该类岩石的发育会受到古湖泊相对水深变化的影响：当水深变化幅度较大时，河流向湖泊内延伸较远，该类岩石在湖岸的发育厚度较厚、发育面积较广；当变化幅度小时，该类岩石发育厚度薄、发育面积较小。在油气勘探领域，需要通过确定该类储油岩石发育的面积与厚度，进而估算出油气资源储量。因此，需要对古代湖泊特定时期的相对水深变化幅度进行定量计算，以此来确定储层岩石的发育情况。同时，在学术研究领域，关于恢复古地貌、古水深的问题一直是地质学、沉积学等领域内研究的热点、难点，该方法对于完善地质学、沉积学的古水深恢复的研究也有积极意义。

前些年曾有国外学者提出利用古海岸斜坡带的古坡度与海岸水上河道沉积的延伸距离来计算相对水深的变化幅度。该方法首先进行水岸边缘斜坡带的斜坡带古坡度的计算，另外还需要根据野外的实地考察来测量出水上河道沉积物在斜坡带向前延伸的距离，也就是沉积物水平延伸距离，利用这两个参数进行三角函数计算，最终计算出相对水深变化幅度。

但现有技术中，在计算相对水深变化幅度时，主要利用的是水上河道沉积物的延伸距离来计算的沉积物水平延伸距离。由于沉积物的水上部分容易被剥蚀、保存不完整，导致水上河道延伸距离不易准确测量。这也就导致了计算出的古河道相对水深变化幅度是不准确的。

技术实现要素：

本发明为申请号为CN201410218974.7，专利名称为“相对水深变化幅度的计算方法”的分案申请。

本发明的目的在于提供一种沉积物水平延伸距离计算方法，以解决现有技术中存在的技术问题。

在本发明的实施例中提供了相对水深变化幅度的计算方法包括：

根据多个地点的砂砾岩百分含量值计算沉积物水平延伸距离；

获取与所述沉积物水平延伸距离相同位置的斜坡带古坡度；

根据所述斜坡带古坡度和所述沉积物水平延伸距离计算相对水深变化幅度。

优选的，所述根据多个地点的砂砾岩百分含量值计算沉积物水平延伸距离包括：

根据第一时期多个地点的砂砾岩百分含量值绘制第一砂砾岩百分含量等值线图；

根据第二时期所述多个地点的砂砾岩百分含量值绘制第二砂砾岩百分含量等值线图；

根据所述第一砂砾岩百分含量等值线图和所述第二砂砾岩百分含量等值线图计算沉积物水平延伸距离。

优选的，还包括：测量指定位置的砂砾岩累计厚度和该位置的地层累计厚度；

根据所述砂砾岩累计厚度和所述地层累计厚度的比值获得所述指定位置的所述砂砾岩百分含量值。

优选的，还包括：

获取沉积颗粒的粒径平均值；

根据测量到的古代水道沉积物残留厚度计算古水道深度；

根据所述粒径平均值和古水道深度计算斜坡带古坡度。

优选的，在所述获取沉积颗粒的粒径平均值前还包括：

获取多个沉积颗粒；

采用直接测量的方式测量每个沉积颗粒的粒径；

若沉积颗粒的粒径小于预设的限度值，则采用仪器测量的方式对该沉积颗粒的粒径进行测量，并得到直接测量值作为粒径测量值；

若沉积颗粒的粒径不小于预设的限度值，则将得到的直接测量值作为粒径测量值；

根据每个沉积颗粒的所述粒径测量值计算粒径平均值。

优选的，所述仪器包括：激光粒度仪和光学显微镜。

优选的，还包括：

测量多期粗粒沉积的厚度；

计算多期所述粗粒沉积的平均值作为古代水道沉积物残留厚度。

优选的，还包括：根据如下公式计算斜坡带古坡度：

S＝0.141×D50×d^-1

其中，S为斜坡带古坡度，D50为沉积颗粒的粒径平均值，d为古水道深度。

优选的，根据如下公式计算相对水深变化幅度；

H＝X×S

其中H为相对水深变化幅度，X为沉积物水平延伸距离，S为斜坡带古坡度。

优选的，采用仪器测量的方式对该沉积颗粒的粒径进行测量包括：

粉碎带有沉积颗粒的岩样，使所述沉积颗粒的粒径大小为0.5-1.5mm；

将粉碎后的岩样置于浓度为10％-20％的H2O2溶液中，并水浴加热预设的一段时间；

取出置于H2O2溶液中的岩样，并将该岩样置于浓度为5％-15％的盐酸溶液中，直至岩样无气泡产生；

取出置于盐酸溶液中的岩样，并去除岩样上的H2O2溶液和盐酸溶液；

研磨所述岩样，以得到独立的沉积颗粒；

使用激光粒度仪测量沉积颗粒的粒径。

本发明实施例提供的相对水深变化幅度的计算方法，与现有技术中的利用水上河道沉积物的延伸距离来计算的沉积物水平延伸距离，由于沉积物的水上部分容易被剥蚀、保存不完整，导致水上河道延伸距离不易准确测量，进而导致相对水深变化幅度是不准确的相比，其通过利用多个地点的砂砾岩百分含量来计算沉积物水平延伸距离，由于砂砾岩是埋藏在水下的，不会受到侵蚀，这样便避免了由于沉积物水上部分容易被剥蚀，而造成的测量不准确，使得计算出沉积物水平延伸距离的可靠性更强，进而使通过斜坡带古坡度和沉积物水平延伸距离计算出的相对水深变化幅度的准确性更强。

附图说明

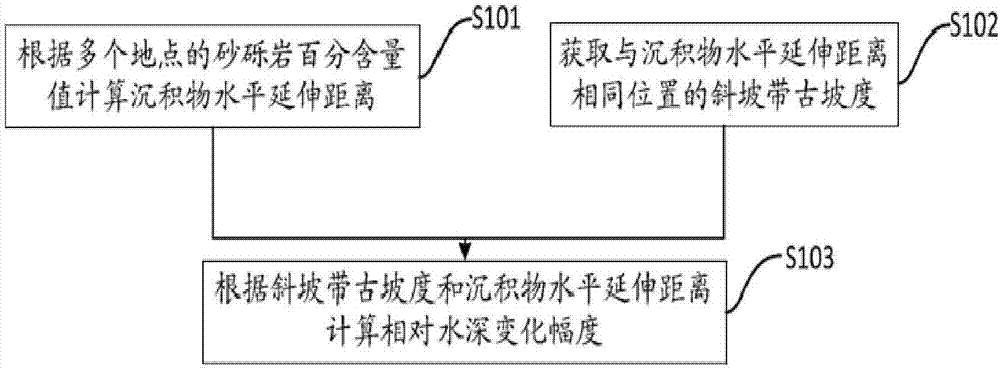
图1示出了本发明实施例的相对水深变化幅度的计算方法的基本流程图；

图2示出了本发明实施例的相对水深变化幅度的沉积物水平延伸距离计算流程图；

图3示出了本发明实施例的相对水深变化幅度的早晚两时期砂砾岩百分含量等值线图的对比图；

图4示出了本发明实施例的相对水深变化幅度计算方法的示意图。

具体实施方式

下面通过具体的实施例子并结合附图对本发明做进一步的详细描述。

本发明实施例1提供了相对水深变化幅度的计算方法，如图1所示，包括如下步骤：

S101，根据多个地点的砂砾岩百分含量值计算沉积物水平延伸距离；

S102，获取与沉积物水平延伸距离相同位置的斜坡带古坡度；

S103，根据斜坡带古坡度和沉积物水平延伸距离计算相对水深变化幅度。

相对水深变化幅度的计算方法主要是利用沉积物水平延伸距离和斜坡带古坡度来计算的，当然沉积物水平延伸距离和斜坡带古坡度指的是同一位置的距离和古坡度，相对水深变化幅度指的是早晚两个时期的水深的差值。

现有技术中，根据野外的实地考察得出的水上沉积物延伸距离计算出的沉积物水平延伸距离是不准确的，其原因是水上沉积物，随着水流的冲击，随着时间的迁移，会使沉积物的水上部分被剥蚀，进而导致计算出的沉积物水平延伸距离是不准确的，有鉴于此，在步骤S101中，采用了使用砂砾岩百分含量值来计算沉积物水平延伸距离，以替代通过水上沉积物延伸距离来计算沉积物水平延伸距离。为了精确计算出沉积物水平延伸距离，需要先测量当地的砂砾岩百分含量，在根据砂砾岩百分含量来计算沉积物水平延伸距离。其中，为了精确的测量砂砾岩的百分含量，需要在待测量的位置打多口探井，当然，探井的位置越密集，所获得的砂砾岩百分含量的数据也就越多，分布越平均，也能够使计算得到的砂砾岩百分含量越精确。在测得砂砾岩百分含量后，可以根据测得的多个位置的砂砾岩百分含量绘制早晚两个时期的砂砾岩百分含量(砂砾岩厚度/地层厚度)等值线图，以更加直观的得到沉积物水平延伸距离。

步骤S102，为了计算出相对水深变化幅度还需要获取斜坡带古坡度，其中，斜坡带古坡度可以根据该位置的古水道深度和平均粒度中值计算得出，现有技术中已经说明其计算过程，在此不再赘述。

步骤S103，最后，根据斜坡带古坡度和沉积物水平延伸距离计算相对水深变化幅度。斜坡带古坡度、沉积物水平延伸距离和相对水深变化幅度组成了一个直角三角形，根据直角三角函数的计算方式即可算得相对水深变化幅度。

本发明实施例提供的相对水深变化幅度的计算方法，通过利用多个地点的砂砾岩百分含量来计算水下沉积物水平延伸距离，其中水下沉积物水平延伸距离是指早晚两个时期的沉积物水平距离的差值。由于砂砾岩是埋藏在水下的，不会受到侵蚀，这样计算，便避免了由于沉积物水上部分容易被剥蚀，而造成的测量不准确，使得计算出沉积物水平延伸距离的可靠性更强，进而使通过斜坡带古坡度和沉积物水平延伸距离计算出的相对水深变化幅度的准确性更强。

本发明实施例2在实施例1的基础上，进一步详细说明的了相对水深变化幅度的计算方法的细节。

为了便于测算出沉积物水平延伸距离，步骤S101可以分为如下步骤，如图2所示：

S201，根据第一时期多个地点的砂砾岩百分含量值绘制第一砂砾岩百分含量等值线图；

S202，根据第二时期所述多个地点的砂砾岩百分含量值绘制第二砂砾岩百分含量等值线图；

S203，根据所述第一砂砾岩百分含量等值线图和所述第二砂砾岩百分含量等值线图计算沉积物水平延伸距离。

需要说明的是，不同时期的砂砾岩百分含量值是通过砂砾岩的粗细程度区分开的，再通过详细的对比和计算以得到不同时期的各个地点的砂砾岩百分含量，最后再根据不同时期的各个地点的砂砾岩百分含量绘制成砂砾岩百分含量等值线图。其中，第一时期和第二时期是指相对水深变化幅度中早晚两个时期。具体的，砂砾岩百分含量值是指定位置的砂砾岩累计厚度和该位置的地层累计厚度之比，也就是每口井的砂砾岩累计厚度和该位置的地层累计厚度之比，当然，砂砾岩累计厚度和地层累计厚度是指的同一时期内的，也就是与需要测算相对水深变化幅度的早晚两时期内的。通过不同位置的井所得出的砂砾岩百分含量值绘制成砂砾岩百分含量等值线图，再通过对比早晚两个时期的砂砾岩百分含量等值线图即可以得到沉积物水平延伸距离。

砂砾岩百分含量等值线图反应了被测算相对水深变化幅度的地域范围内所发育的砂砾岩的含量的多少，而湖泊边缘或海岸边缘的沉积物主要以砂砾岩为主，因此，通过估算砂砾岩等值线的变化，则可反映出湖泊边缘水下沉积物的水平延伸距离。等值线图的编制，首先需搜集研究区域探井所钻取的岩石资料，识别出目的层段内的岩石类别，判断其是否为砂砾岩。然后分别统计每口探井层目的段内的砂砾岩的累计厚度与该目的层段的厚度，并得到其比值，该比值即为每口探井的砂砾岩百分含量值。随后依据不同探井的井位坐标以及该探井的砂砾岩百分含量值，利用制图软件得到等值线图。

岩石粒度的粗细情况来区分并计算绘制好的早晚两个时期的砂砾岩百分含量等值线图的对比图，如图3所示，其中，单、滨及其后面的数字代表不同探井的代号，及多个点的位置代号，黑色区域的边缘即代表湖泊边缘水下沉积物延伸的范围，左侧a图代表水体较深时期沉积物发育的范围，右侧b图代表水体较浅时的范围，虚线即将b图中的范围延伸至a图进行对比，a图中两条实线分别代表水深高、低的不同时期的沉积物范围，在图中测量得到地图上的水下沉积物水平延伸距离变化值，再结合制图时的比例尺，就可换算得到沉积物水平延伸距离X。

斜坡带古坡度可以通过如下步骤计算得出：

获取沉积颗粒的粒径平均值；

根据测量到的古代水道沉积物残留厚度计算古水道深度；

根据所述粒径平均值和古水道深度计算斜坡带古坡度。

其计算公式为S＝0.141×D50×d^-1；

其中，S为斜坡带古坡度，D50为沉积颗粒的粒径平均值，d为古水道深度。

斜坡带古坡度的计算首先要用到圣维南公式(St.Venantequation)：

该方程描述了水道中流体的流动规律。其中，u为x方向(顺流方向)速度，v为y方向(垂直流动方向)速度，t为时间，σ为地势海拔(topographic elevation)，d为古水道深度，τ为剪应力(即颗粒与流体接触界面的剪应力，作用在颗粒表面上，下文中的τ0、τ*同样为颗粒与流体接触界面的剪应力，作用在颗粒表面上)。

将该方程简化：假设水道深度不变，则又另速度保持恒定，既不随时间变化、也不随位置变化，由此可得到则(1)式变为同时，由于其中，S为斜坡带古坡度,所以

τ＝ρgdS， (2)；

(2)式表明了水道水体中的被搬运颗粒达到稳定运动状态下的力学平衡状态，即重力沿斜坡方向的分量同颗粒与流体接触界面的剪应力(内摩擦)达到相等。由于力学平衡，使得颗粒停止运动并实现沉积作用。因此，如果能够估算出剪应力的大小，则可以计算出坡度。

Parker(1978)提出平衡状态下的剪应力τ与颗粒搬运的初始剪应力(临界剪应力)存在着这样的关系：

τ＝(1+ε)τ0， (3)

其中τ0为颗粒搬运的初始剪应力，ε为理论值0.2。Parker认为，颗粒运动受到的剪应力(内摩擦)当满足(3)式所示的关系时，τ值则已达其最大值，在这种情况下，水道自身会建立一种动态平衡的机制，使得颗粒逐渐形成沉积。所以，利用(3)式可以由初始剪应力求得平衡状态下的剪应力。

初始(临界)剪应力的估算可以引入临界Shields剪应力的概念。Croninetal.(2007)指出临界Shields剪应力被定义为颗粒运动的初始剪应力与平均粒度中值的比值，即

其中，τ*为临界Shields剪应力，τ0为颗粒运动初始剪应力，ρs为颗粒密度(砂砾岩密度范围2.3～2.7)，ρ为流体密度(水为1)，D50为平均粒度中值(粒径平均值)。当τ*达到临界值时，颗粒则发生搬运作用。关于τ*的取值，此处选取实验研究的经验值0.062。

联立公式(2)、(3)、(4)，可以得到

将ρs、ρ、ε、τ*分别代入(5)，计算得到坡度计算公式

s＝0.141×D50×d^-1， (6)；

因此，只要测量出研究区的平均粒径平均值D50与古水道深度d，那么斜坡带古坡度S即可得出。

为了更精确的测量沉积颗粒的粒径平均值D50，可以使用测量仪器代替传统的直接测量方式(人工的直尺测量)。同时考虑到仪器测量方式的耗时过长，且成本高于人工的直接测量方式，因此，沉积颗粒的粒径平均值测算方式如下：

获取多个沉积颗粒；

采用直接测量的方式测量每个沉积颗粒的粒径；

若沉积颗粒的粒径小于预设的限度值，则采用仪器测量的方式对该沉积颗粒的粒径进行测量，并得到直接测量值作为粒径测量值；

若沉积颗粒的粒径不小于预设的限度值，则将得到的直接测量值作为粒径测量值；

根据每个沉积颗粒的所述粒径测量值计算粒径平均值。

通过将不同大小的沉积颗粒选择不同的测量方式，提高了测量到的沉积颗粒的粒径的精确度，进而使通过该值计算出的相对水深变化幅度更加准确。同时也避免了一味使用仪器测量而导致的测量时间的延长和成本的增加，又避免了仅仅依靠仪器分析导致粗粒颗粒无法测量的困难。较好的，预设的限度值为10mm，这样可以将通过直接测量方式容易准确测量和不容易准确测量的沉积颗粒区分开。并且有效的提高了测量的速度。较好的，仪器包括：激光粒度仪和光学显微镜。

采用仪器测量的方式对该沉积颗粒的粒径进行测量包括：

粉碎带有沉积颗粒的岩样，使所述沉积颗粒的粒径大小为0.5-1.5mm，较好的，粒径大小为1mm左右；

将粉碎后的岩样置于浓度为10％-20％的H2O2溶液中，并水浴加热预设的一段时间，以除去有机质，较好的，H2O2溶液浓度为15％，预设的一段时间为10分钟左右；

取出置于H2O2溶液中的岩样，并将该岩样置于浓度为5％-15％的盐酸溶液中，直至岩样无气泡产生，较好的，盐酸溶液浓度为10％，以除去胶结物；

取出置于盐酸溶液中的岩样，并去除岩样上的H2O2溶液和盐酸溶液，这样处理，一方面有利于后面操作中对样品的研磨，也可以防止稀盐酸对仪器造成损坏；

研磨所述岩样，以得到独立的沉积颗粒；

使用激光粒度仪测量沉积颗粒的粒径。

至此，待测样品制备完毕，将其放入激光粒度仪内，则可以直接读出粒度大小，也避免了杂质干扰测量的准确性，便可以测量准确的测量出沉积颗粒的粒径。

古水道的深度是利用古代水道沉积物的残留厚度测量。由于水道的水体流速较快、搬运沉积物的能力较强，因此在水道内形成的沉积物多为粒度较粗、颗粒较大的岩石类型。但是，水道的发育有着经常改道的特点，改道之后由于流速减弱、搬运能力减弱，此时形成的沉积物多为粒度较细、颗粒较小的岩石类型。那么，水道的经常性的改道，则导致了钻井得到的岩石类型存在着粗粒与细粒岩石纵向上交互发育的特征。我们通过测量两次细粒岩石之间所夹的粗粒岩石的发育厚度，则可以得到某个时期的水道沉积的厚度，而水道沉积的厚度可以大致反映古水道的深度。在此基础上，测量多期发育的古水道深度，并求取其平均值，以此得到古水道深度，进行随后的计算。

为了更加准确的测算古代水道沉积物残留厚度，可以先测量多期粗粒沉积的厚度；再计算多期所述粗粒沉积的平均值作为古代水道沉积物残留厚度。

沉积物的残留厚度可以间接地反应形成沉积时期的古水道的深度，通过统计地下钻取的岩样中多期粗颗粒沉积的厚度，来测量古水道深度。湖岸水道沉积的特点为多期水道纵向叠加，岩性序列中的粗粒沉积代表水道沉积，而每期粗粒水道间均有细粒沉积作为间隔，因此，应统计每期粗粒沉积发育的厚度，然后求取其平均值作为水道沉积平均残留厚度，进而计算出古水道的深度d，再根据沉积颗粒的粒径平均值D50和古水道深度d计算出斜坡带古坡度S。

如图4所示，在计算出沉积物水平延伸距离X和S后根据如下公式计算相对水深变化幅度；

H＝X×S

其中H为相对水深变化幅度，X为沉积物水下延伸距离，S为斜坡带古坡度。如图4所示，角a的正切值为斜坡带古坡度S。

本发明实施例提供的相对水深变化幅度的计算方法，通过利用多个地点的砂砾岩百分含量来计算沉积物水平延伸距离，由于砂砾岩是埋藏在水下的，不会受到侵蚀，这样便避免了由于沉积物水上部分容易被剥蚀，而造成的测量不准确；并且通过改良了测算沉积颗粒的粒径平均值D50的方式，使用了仪器测量的方式使测量得到的数据的准确性提高了。进而使得计算出沉积物水平延伸距离的可靠性更强，进而使通过斜坡带古坡度和沉积物水平延伸距离计算出的相对水深变化幅度的准确性更强。

以上所述仅为本发明的优选实施例而已，并不用于限制本发明，对于本领域的技术人员来说，本发明可以有各种更改和变化。凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。