边坡地震响应数值模拟中任一方向入射平面体波激振方法与流程

本发明涉及边坡地震响应及稳定性分析领域，尤其涉及边坡地震响应数值模拟中任一方向入射平面体波激振方法。

背景技术：

我国是一个多地震国家，地震诱发的边坡失稳会直接威胁到人民的生命财产安全，因此边坡地震稳定性研究意义重大。然而，地震诱发边坡失稳有很大的不确定性，这种不确定性主要来自边坡自身性状和潜在地震作用两个方面，边坡自身性状属于地震边坡失稳的易发条件，包括边坡岩土体结构和物理力学性质以及边坡几何形状；潜在地震作用属于边坡失稳的诱发因素。对于一个具体的边坡，可以认为边坡的自身性状相对确定，主要的不确定性来自于未来的地震作用，也就是诱发因素。传统工程地震学将地震动力作用归纳为地震动的强度、频率和持续时间，即所谓的“地震动三要素”，对地震动力作用方式(即，地震动力作用方向和作用性质)这一要素考虑够。

目前，在一般场地土层或结构的地震反应分析中，通常假定地震波为S波垂直入射，即场地下水平激振边界上各点的入射地震波动相同且同步水平振动。这对于震源距离较近的场地地震反应问题是合理的，然而对于震源较远(特别是浅源地震并且震源与工程场地有一定距离时)的场地地震反应问题而言，地震波并非垂直入射，而是以一定的方位和入射角向场地入射，场地激振边界各点起振不同步，从而导致场地不同位置地震动呈现出显著的相位差异和地震动力作用性质的变化。当研究对象为大型结构工程或者高边坡时，斜入射引起的地震动力响应与垂直入射相比会有很大的不同。目前，斜入射带来的地震动力响应问题并没有受到足够的重视。

综上所述，当前边坡地震动力响应研究中，地震荷载的输入方法单一，很少考虑地震波从不同方向斜入射的问题，同时也很少考虑不同震相地震波的作用。同时，输入地震波的频率、持时选择和不同震相地震波叠加处理考虑不够完善。因此，在边坡地震动力响应分析中，急需一套任一方向平面体波入射激振的模拟技术。

技术实现要素：

本发明的目的在于针对现有技术的不足，提供一种边坡地震响应数值模拟中任一方向入射平面体波激振的点源叠加模拟技术方法，建立一套任一方向入射平面体波的激振方案。

为实现上述目的，本发明以波传播的惠更斯原理为基础，提供了一种边坡地震响应数值模拟中任一方向入射平面体波激振方法，包括以下步骤：

(1)边坡建模；

(2)根据惠更斯原理分析边坡模型底部激振边界上各节点不同体波震相波动应力时程的启动时序，确定各个节点的启动时差，计算各个节点的启动时刻；

(3)根据不同震相体波的传播特点和偏振特性，获得各震相体波的位移矢量，将波动位移矢量带入几何方程、物理方程，得出各震相地震波激励作用在边坡模型底部激振边界各节点处产生的各应力分量时程表达式；

(4)考虑波传播的实际情况，将边坡模型底部激振边界各节点上不同震相波动的应力时程分量按时序叠加，得到各应力分量的叠加应力时程；

(5)在数值模拟软件中按节点启动时序向边坡模型底部激振边界上各节点输入各应力分量的叠加应力时程；

(6)提取边坡模型的地震动力响应结果，获得边坡地震动力响应云图和监测点的地震动力响应加速度、速度和位移时程。

进一步，步骤(1)具体包括：边坡模型底部激振边界一般设置为水平面(简称为“激振面”)，按一定的网格密度剖分激振边界(边坡模型底层按六面体网格剖分，网格尺寸的大小满足：六面体边长小于入射地震波最高频率对应波长的1/10至1/8)，剖分网格线交点构成激振边界的节点，从而将空间上连续的地震波激振作用离散为激振边界上各个节点的激振作用。

进一步，所述步骤(2)具体包括：当地震波垂直入射时，边坡模型底部激振边界上所有节点同时启动，称这一启动时刻为边坡初动时刻，设置为t₀；当地震波斜入射时，将边坡模型底部激振边界上最先受到地震波扰动的节点称为边坡初动点，该点的启动时刻称为边坡初动时刻，同样设置为t₀，激振边界上任一网格节点p_ij的起振时刻记为t_ij，由下式求得：

式中：t_ij为边坡模型底部激振边界上任一网格节点p_ij的启动时刻，i＝0,1,…,n-1，为该节点在激振面内建立的局部坐标系X方向的序号，i＝0为初动点的序号，X轴正向指向节点序号增加的方向，原点与初动点重合；j＝0,1,…,m-1，为该节点在激振面内建立的局部坐标系Y方向的序号，j＝0为初动点的序号，Y轴正向指向节点序号增加的方向，原点与初动点重合；t₀为边坡初动时刻；l_ij为地震波波前沿入射方向由初动点传至边坡模型底部激振边界上任一节点p_ij所经过的距离，当地震波垂直入射时，l_ij＝0，此时，根据边坡激振面的具体情况，可将局部坐标系原点设置在激振面的某个角点上，将激振面置于该局部坐标系的第一象限；c为边坡激振边界以下介质的弹性波速，纵波取c_P，横波取c_S；无论地震波垂直入射还是斜入射，边坡初动时刻t₀都等同于地震波到达边坡的时刻。

进一步，步骤(3)中，各体波震相包括：纵波(P，所引起的质点振动位移方向与波传播方向一致)、横波(S，所引起的质点振动位移方向与波传播方向正交)；考虑横波振动矢量与体波入射面(体波射线与边坡底部激振面法线决定的平面，为铅垂面)的关系，可将横波振动矢量进一步分解为入射面内的振动分量SV波和垂直于入射面的振动分量SH波；再考虑各体波震相(P、SV、SH)波动位移的初动方向，P波可分为初动向前的压缩波P⁺和初动向后的拉伸波P^-；沿波传播方向向前看，在入射面内观察SV波、垂直于入射面观察SH波，SV和SH波均可分为初动向右的右剪波SV⁺、SH⁺和初动向左的左剪波SV^-、SH^-。

进一步，步骤(4)中，边坡模型底部激振边界上各节点不同体波震相波动的应力时程按分量叠加包括两种震相的叠加(12种：P⁺+SV⁺、P⁺+SV^-、P^-+SV⁺、P^-+SV^-、P⁺+SH⁺、P⁺+SH^-、P^-+SH⁺、P^-+SH^-、SV⁺+SH⁺、SV⁺+SH^-、SV^-+SH⁺、SV^-+SH^-)和三种震相的叠加(8种：P⁺+SV⁺+SH⁺、P⁺+SV⁺+SH^-、P⁺+SV^-+SH⁺、P⁺+SV^-+SH^-、P^-+SV⁺+SH⁺、P^-+SV⁺+SH^-、P^-+SV^-+SH⁺、P^-+SV^-+SH^-)共计20种情况，叠加公式根据步骤(3)进一步推导而来；在进行不同体波震相应力分量时程叠加时，应首先确定各节点上各个震相的到达时刻和持续时间，然后按节点上各个震相的启动时序完成边坡模型底部激振边界上各个节点处不同体波震相波动应力分量时程叠加，获得各节点处体波震相波动应力分量叠加时程。

进一步，步骤(5)中，将经步骤(4)获得的体波震相波动应力分量叠加时程按启动时序加载到激振面的各个节点上。

进一步，步骤(6)中，自边坡初动时刻t₀起，数值模拟系统即开始记录边坡模型中各个节点的地震动力响应过程，并根据研究需要提取不同时刻的边坡地震动力响应云图以及边坡模型任一监测点的地震动力响应加速度、速度和位移时程。

与现有技术相比，本发明的有益效果是：通过提供一种能在边坡地震响应数值模拟中实现任一方向入射平面体波激振的方法，建立一套边坡受任一方向入射平面体波激励的数值模拟方案，以揭示特定边坡地震破坏的多样性，进而估算特定方式边坡破坏的可能性。

附图说明

图1为本发明边坡地震响应数值模拟中任一方向斜入射平面体波激振方法的流程图。

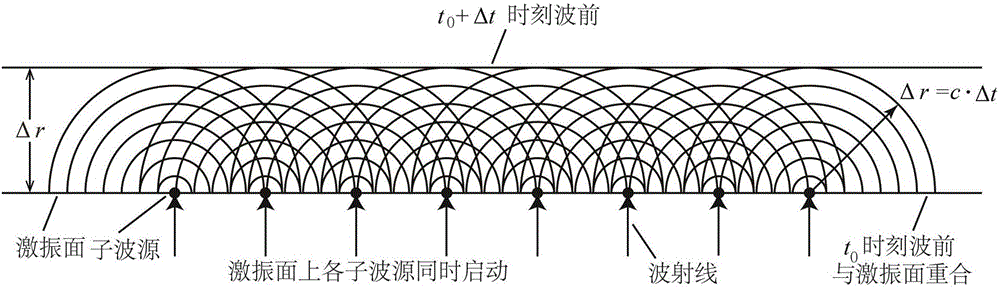
图2为本发明边坡地震响应数值模拟中垂直入射平面体波激振的惠更斯原理示意图。

图3为本发明边坡地震响应数值模拟中斜入射平面体波激振的惠更斯原理示意图。

图4为本发明边坡地震响应数值模拟中任一方向斜入射平面体波激振边坡底部节点启动时序分析示意图。

图5为本发明边坡地震响应数值模拟中任一方向斜入射平面体波射线和波动位移矢量与边坡底部水平激振边界在入射面内的空间关系示意图。

图6为本发明边坡地震响应数值模拟中任一方向斜入射平面体波射线及位移矢量在边坡底部水平激振面内的投影关系示意图。

图7为本发明边坡地震响应数值模拟中任一方向斜入射平面体波激振的P波位移分量(u_P,v_P,w_P)与位移矢量模(S_P)的关系示意图。

图8为本发明边坡地震响应数值模拟中任一方向斜入射平面体波激振的SV波位移分量(u_V,v_V,w_V)与位移矢量模(S_V)的关系示意图。

图9为本发明边坡地震响应数值模拟中任一方向斜入射平面体波激振的SH波位移分量(u_H,v_H,w_H)与位移矢量模(S_H)的关系示意图。

图10为本发明边坡地震响应数值模拟中垂直入射平面横波位移分量(u_S,v_S,w_S＝0)与位移矢量模(S_S)的关系示意图。

具体实施方式

下面将对本发明的具体实施方式进行详细说明，但应当说明的是，这些实施方式并非对本发明的限制，本领域普通技术人员根据这些实施方式所作的功能、方法、或者结构上的等效变换或替代，均属于本发明的保护范围之内。

如图1至图10所示：图1为本发明边坡地震响应数值模拟中任一方向斜入射平面体波激振方法的流程图；图2为本发明边坡地震响应数值模拟中垂直入射平面体波激振的惠更斯原理示意图；图3为本发明边坡地震响应数值模拟中斜入射平面体波激振的惠更斯原理示意图；图4为本发明边坡地震响应数值模拟中任一方向斜入射平面体波激振边坡底部节点启动时序分析示意图；图5为本发明边坡地震响应数值模拟中任一方向斜入射平面体波射线和波动位移矢量与边坡底部水平激振边界在入射面内的空间关系示意图；图6为本发明边坡地震响应数值模拟中任一方向斜入射平面体波射线及位移矢量在边坡底部水平激振面内的投影关系示意图；图7为本发明边坡地震响应数值模拟中任一方向斜入射平面体波激振的P波位移分量(u_P,v_P,w_P)与位移矢量模(S_P)的关系示意图；图8为本发明边坡地震响应数值模拟中任一方向斜入射平面体波激振的SV波位移分量(u_V,v_V,w_V)与位移矢量模(S_V)的关系示意图；图9为本发明边坡地震响应数值模拟中任一方向斜入射平面体波激振的SH波位移分量(u_H,v_H,w_H)与位移矢量模(S_H)的关系示意图；图10为本发明边坡地震响应数值模拟中垂直入射平面横波位移分量(u_S,v_S,w_S＝0)与位移矢量模(S_S)的关系示意图。

本实施方式提供了一种边坡地震数值模拟中任一方向入射平面体波激振方法，具体步骤如下：

步骤S1，边坡建模

边坡建模可以利用多种建模软件和工具，可以建成复杂的实体三维模型或者是简单的二维模型，但建模过程中需要注意的是：数值模型的边坡底部激振边界设置为水平面，简称为“激振面”，按一定要求，激振边界按一定的网格密度进行剖分(边坡模型底层按六面体网格剖分，网格尺寸的大小满足：六面体边长小于入射地震波最高频率对应波长的1/10至1/8)，剖分网格线交点构成激振边界的节点，从而将空间上连续的地震波激振作用离散为激振边界上各个节点的激振作用。

步骤S2，任一方向入射地震平面体波激励在边坡模型底部激振边界上各节点的启动时序计算。

本步骤的理论基础为波传播的惠更斯原理。如图2、图3所示，惠更斯原理可表述为：介质中任意时刻t₀波前面上的各点，都可看作可发射子波的波源，这些子波源向介质中发射球面子波，球面子波按子波源附近介质的波速c向前推进，经过一个很小的时间增量Δt后的下一时刻t₀+Δt，球面子波波前离开子波源的距离为Δr＝c·Δt，此时，在波前进方向上所有子波波前的包络面就是时刻t₀+Δt对应的新的波前面。

图2可以说明地震波垂直向上入射到边坡模型内的情况。在t₀时刻地震波垂直入射时，边坡模型底部所有节点同时发生振动，这些节点可以看作子波波源，地震波在边坡模型内向上传播，在t₀+Δt时刻，波前传到模型网格倒数第二层节点，致使模型第二层节点也同时发生振动。这样地震波就在边坡内垂直向上传播开来。

同样，利用惠更斯原理可以解决地震波斜入射问题。如图3所示，边坡初动时刻为t₀，边坡底部激振边界上每一个节点均可以看作子波波源，在数值模拟软件中，可以设置边坡模型底部激振边界上各节点按启动时序依次起振，两相邻节点的起振时间间隔为Δt′(与相邻节点间距有关)，由于边坡模型底部各节点起振时刻不同，经时间Δt后，新产生的波前会与边坡底部激振面呈一定夹角(当激振面上下介质波速相等时，此夹角与体波入射角相等)，从而实现了地震体波的斜入射激振。

如图4所示，边坡底部激振面网格剖分线与坐标轴x、y平行。与x轴平行的一组网格剖分线序号记为i，i＝0,1,…,n-1，共计n条；与y轴平行的一组网格剖分线序号记为j，j＝0,1,…,m-1，共计m条。两组剖分网格线相交形成一系列节点p_ij，节点数目共计m×n个，自地下任一方向入射的地震平面体波使得这些节点按一定时序陆续启动。如图4所示，将边坡底部激振边界上最先受到扰动的节点设为xy平面坐标原点。为表达方便，也将该节点称为边坡初动点，并记其起振时刻为t₀；记边坡底部激振边界内任意网格节点p_ij的起振时刻为t_ij。由图4可知，当入射方位角为α时，波前面由初动点o沿入射方向传至节点p_ij时，波动传播距离即为t₀时刻和t_ij时刻两个波前之间的距离li_j：

l_ij＝|oq|·sinθ＝(iΔx cosα+jΔy sinα)·sinθ (a)

因此，任意网格节点p_ij的起振时刻t_ij为：

式中：i＝0,1,…,n-1；j＝0,1,…,m-1；t₀为边坡初动点波动到时；c为边坡激振边界以下介质的弹性波速，纵波取c_P，横波取c_S。

由于体波震相的传播波速主要分为纵波波速c_P和横波波速c_S两种，因此从运动学角度考虑，对于激振边界节点震相叠加而言，只要考虑纵波和横波两种基本震相就可以满足叠加分析需要了。

考虑纵波(P波)入射，式(b)可写为：

式中，t_Pij为P波震相在节点p_ij的启动时刻；t_P0为边坡初动点的P波扰动到时。

考虑横波(S波，包括SV和SH)入射，式(b)可写为：

式中，t_Sij为S波震相在节点p_ij的启动时刻；t_S0为边坡初动点的S波扰动到时。

由于恒有c_P＞c_S，因此对同一节点而言，恒有t_Pij＜t_Sij。同样，恒有t_P0＜t_S0。

设震源到边坡初动点之间的距离为R，则t_P0和t_S0分别由式(c)和式(d)计算：

t_P0＝R/c_P0 (c)

t_S0＝R/c_S0 (d)

按式(c)和式(d)，可将弹性波速c_P0和c_S0视为地震震源和边坡所在区域地壳介质的等效平均波速。从震源辐射波场的角度考虑，从宏观上观察边坡所在区域波场中的位置，则可以进一步深入研究因边坡在波场中空间位置不同而导致的边坡地震动力响应的变化。由式(c)和式(d)可见，由边坡初动点的纵波、横波到时可以求算出边坡与震源之间的距离R，如式(e)所示：

R＝Δt_PS0·c_Φ (e)

式中，Δt_PS0＝t_S0-t_P0，是地震横波和纵波到达边坡的到时差；称为边坡及震源所在区域地壳介质的虚波速度。

步骤S3，不同震相平面体波激励作用在边坡模型底部各节点处产生的应力分量时程计算。

步骤S3可以具体分为以下几个步骤来实现：

1)求波动方程的位移解

设地震波扰动在介质中任一点(x,y,z)处引起如式(1)所示的质点位移

其中，u,v,w分别为波动位移在x,y,z三个方向上的位移分量，均为空间坐标(x,y,z)和时间t的函数：

u＝u(x,y,z,t)；v＝v(x,y,z,t)；w＝w(x,y,z,t)

设位移矢量的模为S，即：

根据弹性波动理论，在弹性介质中的地震波传播可以用式(2)所示的波动方程描述：

式中，ρ为介质密度；μ为剪切模量；λ与μ合成拉梅常数，拉梅常数与介质弹性模量E和泊松比v的关系为：

对于介质空间中的任一质点，可以证明，式(3)所示的单频简谐波动位移是波动方程(2)的一个通解：

式中，A_ω＝A_ω(x,y,z)为简谐波动的振幅，在某一具体介质点(x,y,z)处的一定范围内可近似为常数；i为虚单位，为波动的相位函数，其中ω为波动圆频率，与频率f之间的关系为ω＝2πf；为介质中任一点(x,y,z)的位置向量，为波矢量，波矢量的方向与波传播方向相同，波矢量的模称为波数，其中c为波动在介质中的传播速度，分为纵波波速c_P和横波波速c_S。纵波波速c_P、横波波速c_S与介质密度ρ以及拉梅常数λ、μ之间的关系为：

根据傅里叶原理，对于任意非简谐波动位移S＝S(x,y,z,t)，均可由如式(3)所示的不同频率简谐波动位移叠加而成。即：

因非简谐波动的传播方向与其个简谐分量波动的传播方向相同，因此非简谐波的波矢量与其各简谐分量波动的波矢量指向相同，但非简谐波动波数与其各简谐分量波动的波数不一定相等。后面的分析中将不区分与两者都写为

同样可以证明，式(4)所示的混频非简谐波动位移也是波动方程(2)的一个解。

2)推导各体波震相的波动位移分量表达式

边坡地震反应数值模拟中，边坡数值模型的激振边界通常设置在边坡底部，界面为水平面，可称为激振面。边坡模型局部坐标系(x,y,z)的设置：z轴铅垂向上，x、y轴位于激振平面内，x轴沿边坡梯度最大方向指向坡外，坐标原点视具体情况置于激振面的某个角点上；x、y、z三轴相互正交形成右手直角坐标系。

设边坡受到自地下任一方向入射的地震平面体波激振，体波震相包括P波、SV波和SH波三种，不同震相的入射方位、初动位移矢量相对于边坡模型局部坐标系的空间关系如图5、图6所示。

图5所示为在入射面内观察体波自下而上斜入射至边坡底部的情况。坐标轴z与激振平面垂直指向上，坐标轴r就是在激振面内，与入射面和激振面的交线重合，r轴指向与入射波射线方向在激振面内的投影方向一致。入射波射线与激振面法线之间的夹角θ称为地震波入射角。

如图6所示，在激振面内，r轴方向与波射线在激振面内的投影方向一致，射线水平投影方向与x轴方向之间的夹角α称为地震波入射方位角。r轴上任一点r在x轴和y轴上的投影分别为x和y，在量值上，r与x、y之间存在如下关系：

与波传播方向一致的波矢量在图5、图6所示的边坡局部坐标系中可分解为k_x,k_y,k_z三个分量，即其中：

式(3)所示简谐波动位移的相位函数可具体展开为：

图5、图6所示几种体波震相振动位移矢量与波射线表明了地震波动位移方向与波传播方向的几何关系。

P波引起的质点振动位移沿着波传播的方向，对波传播前方介质产生压缩或拉伸作用。P波位移初动可分为与波传播方向相同和相反两种：与波传播方向相同的P波初动向前推，对前方介质产生压力，称为压缩波，记为P⁺；与波传播方向相反的P波初动向后拉，对前方介质产生拉力，称为拉伸波，记为P^-。

SV波引起的质点振动位移在入射面内垂直于波传播方向，对前方介质产生剪切作用。在入射面内沿波传播方向向前看，SV波位移初动可分为向右和向左两种：初动向右的SV波可简称为右剪SV波，记为SV⁺；初动向左的SV波可简称为左剪SV波，记为SV^-。

SH波引起的质点振动位移垂直于入射面和波传播方向，质点振动方向恒为水平，对前方介质同样产生剪切作用。沿波传播方向向前看，SH波位移初动可分为水平向右和水平向左两种：初动水平向右的SH波可简称为右剪SH波，记为SH⁺；初动水平向左的SH波简称为左剪SH波，记为SH^-。

根据不同震相波动位移方向与波传播方向的关系以及波射线与边坡模型局部坐标系的关系，按矢量投影的方法，可以推导出不同震相位移分量u,v,w与波动位移矢量模S之间的关系。

P波位移分量

图7所示为P波位移分量u_P、v_P、w_P与压缩波P⁺位移矢量模S_P⁺及拉伸波P^-位移矢量模S_P^-之间的几何关系示意图。

设压缩波P⁺和拉伸波P^-的位移矢量大小相等、方向相反，则P⁺的位移矢量模S_P⁺和P^-的位移矢量模S_P^-之间的关系为：

S_P⁺＝-S_P^-＝S_P

据此，纵波P(压缩波P⁺和拉伸波P^-)的位移分量u_P、v_P、w_P与位移矢量模S_P的关系分别如式(7)和式(8)所示。

压缩波P⁺的位移分量：

拉伸波P^-的位移分量：

按照式(3)、式(4)，式(7)、式(8)中S_P不仅可以代表图7中所示的P⁺和P^-震相波动的初动矢量模，同时也可代表初动分别为向前或向后的P波位移矢量时程的模，分为单频简谐波动和任意非简谐波动两种，分别如式(9)和式(10)所示：

S_P＝S_P(x,y,z,t) (10)

式中，A_P＝A_P(x,y,z)为简谐波动的振幅，在点(x,y,z)附近一定范围内可视为常数；为P波的波矢量，波数其中c_P为纵波波速。

SV波位移分量

图8所示为SV波位移分量u_V、v_V、w_V与右剪SV波SV⁺的位移矢量模S_V⁺及左剪SV波SV^-的位移矢量模S_V^-之间的几何关系示意图。

设右剪SV波SV⁺和左剪SV波SV^-的位移矢量大小相等、方向相反，则SV⁺波的位移矢量模S_V⁺和SV^-波的位移矢量模S_V^-之间的关系为：

S_V⁺＝-S_V^-＝S_V

据此，SV波(SV⁺和SV^-)的位移分量u_V、v_V、w_V与位移矢量模S_V的关系分别如式(11)和式(12)所示。

右剪波SV⁺的位移分量：

左剪波SV^-波的位移分量：

与P波类似，式(11)、式(12)中的位移矢量模S_V不仅可以代表SV波位移初动矢量的模，同时也可代表右剪或左剪SV波位移矢量时程的模，分为单频简谐波动式(13)和任意非简谐波动式(14)：

S_V＝S_V(x,y,z,t) (14)

式中，A_V＝A_V(x,y,z)为简谐波动的振幅，在点(x,y,z)附近一定范围内可视为常数；为横波(SV波)的波矢量，波数其中c_S为横波波速。

SH波位移分量

图9所示为SH波位移分量u_H、v_H(w_H≡0)与右剪SH波SH⁺的位移矢量模S_H⁺及左剪SH波SH^-的位移矢量模S_H^-之间的几何关系在水平面内的示意图。

设右剪SH波SH⁺和左剪SH波SH^-的位移矢量大小相等、方向相反，则SH⁺波的位移矢量模S_H⁺和SH^-波的位移矢量模S_H^-之间的关系为：

S_H⁺＝-S_H^-＝S_H

据此，SH波(SH⁺和SH^-)的位移分量u_H、v_H(w_H≡0)与位移矢量模S_H的关系分别如式(15)和式(16)所示。

右剪波SH⁺的位移分量：

左剪波SH^-的位移分量：

同样，式(15)、式(16)中的位移矢量模S_H不仅可以代表SH波位移初动矢量的模，同时也可代表右剪和左剪SH波位移矢量时程的模，分为单频简谐波动式(17)和任意非简谐波动式(18)：

S_H＝S_H(x,y,z,t) (18)

式中，A_H＝A_H(x,y,z)为简谐波动的振幅，在点(x,y,z)附近一定范围内可视为常数；为横波(SH波)的波矢量，波数其中c_s为横波波速。

3)求解体波震相的波动应力

在边坡局部坐标系中，边坡底部激振边界上的波动应力分量有三个：σ_z、τ_zx和τ_zy。根据弹性力学中的几何方程(应变-位移关系)和物理方程(应力-应变关系)，可以得到波动应力分量σ_z、τ_zx、τ_zy与波动位移分量u、v、w之间的关系，如式(19)所示：

将式(7)～式(18)所示的各个体波震相的位移分量代入上式，即可得到不同体波震相的波动应力分量与波动位移分量之间的关系表达式。

由式(19)可知，波动应力分量σ_z、τ_zx、τ_zy的计算涉及到的位移分量偏导数有对各个体波震相的位移分量求这些偏导数，代入式(19)，即可确定出各体波震相波动应力分量与波动位移分量之间的表达式。

由式(7)～式(18)可以看出，各个体波震相位移分量都可表示为震相位移向量在x,y,z三个方向的投影，归根结底，真正控制位移分量变化的是位移矢量模的变化。而不同体波震相位移矢量时程的模均可归纳为单频简谐波动和任意非简谐波动两种形式，并可统一表示为：

S＝S(x,y,z,t) (21)

对P波，S＝S_P，A＝A_P，对SV波，S＝S_V，A＝A_V，对SH波，S＝S_H，A＝A_H，

对波动位移分量的几个偏导数都可归结为对波动位移矢量模的偏导数

先对简谐波动进行分析。

式(20)分别对空间变量x,y,z求导，有：

把式(5)代入式(22)，并考虑和有：

另外，波动位移(质点位移)矢量的模S对时间的导数为波动速度(质点振动速度)的模V，即

式(20)对时间t求导得：

式中，V＝V(x,y,z,t)为地震波动在点(x,y,z)处引起的质点振动速度(波动速度)矢量时程的模。对P波，V＝V_P＝V_P(x,y,z,t)，S＝S_P，A＝A_P，对SV波，V＝V_V＝V_V(x,y,z,t)，S＝S_V，A＝A_V，对SH波，V＝V_H＝V_H(x,y,z,t)，S＝S_H，A＝A_H，

把式(23)代入式(22)得：

式中，c为地震波传播的速度，纵波(P波)c＝c_P，横波(SV、SH波)c＝c_S；V为地震波在点(x,y,z)引起的质点振动速度矢量时程的模(简称为振速时程)。按式(23)，V的振动方式为简谐振动，可写为如下形式：

式中，V_m＝-ω·A为质点振速的振幅(振速最大值)，其中ω为质点振动的圆频率，A为质点振动的位移振幅(位移最大值)。对于P波，V_m＝V_mP＝-ω·A_P；对于SV波，V_m＝V_mV＝-ω·A_V；对于SH波，V_m＝V_mH＝-ω·A_H。

与波动位移的简谐振动式(3)可推广为非简谐振动式(4)类似，根据傅里叶原理，式(25)所示波动速度的简谐振动过程同样可以推广为非简谐振动过程，如式(26)所示：

V＝V(x,y,z,t)＝V_m·f(x,y,z,t) (26)

式中，V_m为点(x,y,z)处非简谐质点振速时程的最大振速值，或称为峰值振速；f(x,y,z,t)＝V/V_m为点(x,y,z)处最大值为1的归一化(无量纲)质点振速时程。

P波应力分量

压缩波P⁺的应力分量

对式(7)所示P⁺波的位移分量求偏导数再把式(24)所示对位移矢量模的偏导数代入得：

将以上偏导数代入式(19)得到压缩波P⁺的应力分量，如式(27)所示：

拉伸波P^-的应力分量

对式(8)所示P^-波的位移分量求偏导数再把式(24)所示对位移量模的偏导数代入得：

将以上偏导数代入式(19)得到拉伸波P^-的应力分量，如式(28)所示：

SV波应力分量

右剪波SV⁺的应力分量

对式(11)所示SV⁺波的位移分量求偏导数再把式(24)所示对位移矢量模的偏导数代入得：

将以上偏导数代入式(19)得到右剪波SV⁺的应力分量，如式(29)所示：

左剪波SV^-的应力分量

对式(12)所示SV^-波的位移分量求偏导数再把式(24)所示对位移矢量模的偏导数代入得：

将以上偏导数代入式(19)得到左剪波SV^-的应力分量，如式(30)所示：

SH波应力分量

右剪波SH⁺的应力分量

对式(15)所示SH⁺波的位移分量求偏导数再把式(24)所示对位移矢量模的偏导数代入得：

将以上偏导数代入式(19)得到右剪波SH⁺的应力分量，如式(31)所示：

左剪波SH^-的应力分量

对式(16)所示SH^-波的位移分量求偏导数再把式(24)所示对位移矢量模的偏导数代入得：

将以上偏导数代入式(19)得到左剪波SH^-的应力分量，如式(32)所示：

特别的，当地震波垂直入射时，入射角θ为0°，即边坡底部激振边界上所有节点同时起振。根据式(27)、式(28)，此时P波只有z向的应力分量不为0，即：

当S波垂直入射时，由上述表示S波应力分量的公式可知，参数α并不能像P波垂直入射的应力公式一样直接消去。而此时，根据前述对方位角α的定义，其已不能表达入射波射线与边坡的实际方位关系了。因此，S波垂直入射时的应力分量公式需要根据S波垂直入射时的偏振位移情况重新推导。

若横波的偏振在介质中某点(x,y,z)引起的位移为其模为S_S。如图10所示，设由x轴正向逆时针旋转至横波振动初动方向的夹角为β(0°≤β＜360°)，则有：

由上式与式(11)、式(12)的对比可知，横波垂直入射时，其位移分量在形式上与横波斜入射时SV波的位移分量式类似。采用相同的应力分量时程函数推导过程，易得横波垂直入射情况下，其应力分量如下所示：

步骤S4，边坡模型底部激振边界各节点不同体波震相波动应力分量的叠加时程计算。

考虑式(b′)和式(b″)所示节点p_ij的P波和S波启动时刻t_Pij和t_Sij，式(27)～式(32)所示的P(P⁺，P^-)、SV(SV⁺，SV^-)和SH(SH⁺，SH^-)的波动应力时程表达式可写为式(27′)～式(32′)。

①P波应力分量时程(t≥t_Pij)

压缩波P⁺的应力分量时程。

拉伸波P^-的应力分量时程。

②SV波应力分量时程(t≥t_Sij)

右剪波SV⁺的应力分量时程

左剪波SV^-的应力分量时程

③SH波应力分量时程(t≥t_Sij)

右剪波SH⁺的应力分量时程

左剪波SH^-的应力分量时程

按波动位移方向与波射线的关系，到达激振边界的体波震相有P、SV和SH三种，进一步考虑波动的初动位移方向，又可进一步分为P⁺，P^-；SV⁺，SV^-；SH⁺，SH^-六类。从波传播的物理实际考虑，到达激振边界任一节点处可能发生的波动震相组合包括两种震相组合和三种震相组合。

①两种震相组合(12种)

P⁺+SV⁺，P⁺+SV^-；P^-+SV⁺，P^-+SV^-；

P⁺+SH⁺，P⁺+SH^-；P^-+SH⁺，P^-+SH^-；

SV⁺+SH⁺，SV⁺+SH^-；SV^-+SH⁺，SV^-+SH^-。

有12种组合。

②三种震相组合(8种)

P⁺+SV⁺+SH⁺，P⁺+SV⁺+SH^-；P⁺+SV^-+SH⁺，P⁺+SV^-+SH^-；

P^-+SV⁺+SH⁺，P^-+SV⁺+SH^-；P^-+SV^-+SH⁺，P^-+SV^-+SH^-。

考虑上述可能的震相组合，选择相应的应力分量时程公式，取对应分量的代数和，即可得到激振面节点p_ij上不同体波震相波动应力分量的叠加时程表达式。譬如，两种震相组合P⁺+SV⁺在节点p_ij上的输入波动应力分量σ_{z P}⁺_+V⁺(p_ij)、τ_{zx P}⁺_+V⁺(p_ij)和τ_{zy P}⁺_+V⁺(p_ij)为式(27′)和式(29′)对应应力分量时程的代数和：

对σ_zP⁺(t-t_Pij)，t≥t_Pij；对σ_zV⁺(t-t_Sij)，t≥t_Sij。即：

对V_P(t-t_Pij)，t≥t_Pij；对V_V(t-t_Sij)，t≥t_Sij。

步骤S5，边坡模型底部激振边界各节点体波震相波动应力分量叠加时程输入

以单频简谐波动输入为例，可按上述式(27)～式(32)公式输入即可。

简谐P波、S波叠加组合数值模拟也采用上节提到的动力输入方案。首先确定P波、S波的频率、振幅、到时与持时等因素。根据计算出来的P波和S波的作用时间，输入各时间段的应力时程。

以FLAC^3D软件为例，现列举出简谐P波、SV波叠加入射的命令流示例：

其中，dingyi1x.txt、dingyi2y.txt、dingyi3z.txt，定义的是P波和S波从某个方向输入的三分量波函数FISH语言表达式。call shijia1.txt、call shijia2.txt、call shijia3.txt定义的是P波、S波从某个方向输入的三分量应力时程表达式。

步骤S6，边坡模型地震动力响应模拟结果提取

自边坡模型底部激振边界体波震相波动应力分量叠加时程加载(边坡初动时刻t₀)起，数值模拟系统即刻开始记录边坡模型中各个节点的地震动力响应过程，并根据研究需要提取不同时刻的边坡地震动力响应云图以及边坡模型任一监测点的地震动力响应加速度、速度和位移时程。

本发明通过计算边坡模型底部激振边界上各节点受地震动力荷载作用的启动时序，将地震波的垂直入射和斜入射问题转化为边坡底部激振边界上各节点的启动时序问题；利用单元体运动方程、几何方程和物理方程(虎克定律)，推导出用位移表示的三维波动方程；根据不同震相地震波的传播特点和偏振特性，得出各震相地震波的位移矢量，将位移矢量带入几何方程和虎克定律，计算出各震相地震波激励在边坡底部激振边界上各个节点处产生的应力分量时程表达式，建立起一套边坡受任一方向入射地震平面体波激励的边坡激振方案，可以揭示特定边坡地震破坏的多样性，进而估算特定方式的边坡破坏的可能性。

上文所列出的一系列详细说明仅仅是针对本发明的可行性实施方式的具体说明，它们并非用以限制本发明的保护范围，凡未脱离本发明技艺精神所作的等效实施方式或变更均应包含在本发明的保护范围之内。

对于本领域技术人员而言，显然本发明不限于上述示范性实施例的细节，而且在不背离本发明的精神或基本特征的情况下，能够以其他的具体形式实现本发明。因此，无论从哪一点来看，均应将实施例看作是示范性的，而且是非限制性的，本发明的范围由所附权利要求而不是上述说明限定，因此旨在将落在权利要求的等同要件的含义和范围内的所有变化囊括在本发明内。