一种绕飞轨迹下的旋翼无人机三维目标定位方法与流程

本发明属于视觉测量领域，具体涉及一种绕飞轨迹下的旋翼无人机三维目标定位方法。
背景技术：
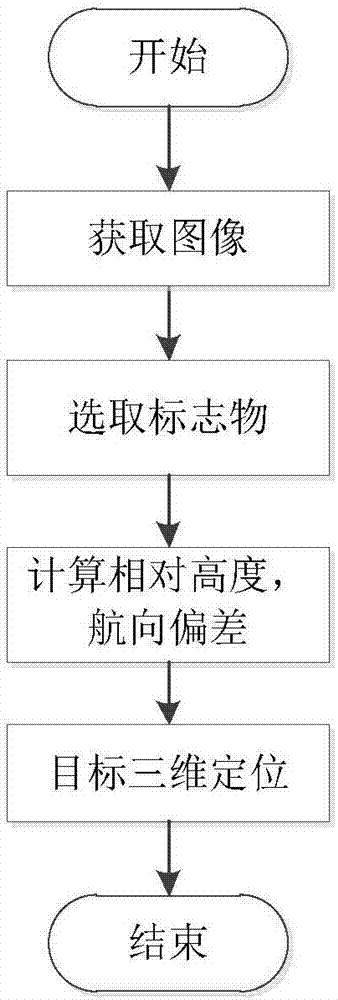
：旋翼无人机以成本低、垂直起降和空中悬停等特点，在侦查、农业保险、环保和灾后救援等领域获得了广泛应用。而基于视觉的旋翼无人机目标定位已是目前的研究热点问题之一，采用视觉方法对目标进行三维定位，首先通过三角定位方法确定无人机与目标的相对高度，然后才能进行目标的定位。考虑到旋翼无人机配备的低精度ahrs航姿参考系统所带来的航向偏差较大，利用无人机拍摄的图像进行视觉测量时，图像中投射的光线均发生一定的偏移。若采用传统的三角定位方法,从左右视图投射的两组光线由于发生了偏移，求解得到的相对高度将产生较大的误差，故无法准确计算无人机与物体间的相对高度，从而不能对目标进行有效的三维定位。技术实现要素：有鉴于此，本发明提供了一种绕飞轨迹下的旋翼无人机三维目标定位方法，能够计算得到航向偏差，减小对相对高度的计算误差，从而提高旋翼无人机对目标的三维定位能力。有益效果：(1)本发明所提供的方法针对配备低精度ahrs航姿参考系统系统的旋翼无人机，能精确地计算ahrs航姿参考系统存在的航向偏差，进而计算绕飞轨迹下旋翼无人机与目标所在地形之间的高度，从而实现旋翼无人机对目标的三维视觉定位。附图说明图1为本发明的旋翼无人机目标三维定位系统结构图；图2为本发明所提供方法的流程图；图3为本发明所使用的旋转视图双目视觉模型示意图；图4为本发明所使用的单目摄像机测距模型示意图；图5为本发明所提供方法中的迭代过程流程图；图6为本发明所提供方法中的的数据拟合曲线；图7为本发明所提供方法中的的数据拟合曲线；图8为本发明所提供方法的定位效果图。具体实施方式下面结合附图并举实施例，对本发明进行详细描述。搭建如下实验平台对本发明的有效性进行验证，使用一架t650四旋翼无人机，一台笔记本作为地面站，无人机与地面站之间可进行实时通信，系统结构如图1所示。对于无人机，机上带有gps定位系统、ahrs航姿参考系统、高程计、无线图像传输模块和无线数据收发模块，使3drobotics公司的apm飞行控制系统工作在自稳模式来保证无人机的稳定飞行。在无人机的机头位置安装摄像机，俯视角β为45°，并通过无线图像传输模块回传图像到地面站，而由gps定位系统、ahrs航姿参考系统和高程计分别获得的无人机的位置、姿态和高程信息则通过无线数据收发模块传输到地面站。地面站以计算机为主体，运行无人机视觉定位等算法，使用usb接口连接无线数据收发模块，实现无人机与地面站的相互通信。基于该实验平台，如图2所示，一种绕飞轨迹下的旋翼无人机三维目标定位方法，包括以下步骤：步骤一、系统启动后，利用搭载在无人机上的摄像机拍摄图像，并将图像回传到地面站；步骤二、从回传的图像中选择具有清晰轮廓的静态物体作为标志物，并对标志物进行视觉识别；步骤二中对于标志物进行视觉识别的具体过程如下：运用sift算法对标志物进行识别，得到m个特征点p1,p2...pm-1,pm，并将这些特征点进行存储作为模板，m为整数；步骤三、旋翼无人机以该标志物为中心绕飞，并利用视觉识别的结果对标志物进行多点图像测量，基于双目视觉模型和线性回归模型相互迭代的方法计算无人机相对于目标所在地形的高度和航向偏差；步骤三的流程图如图5所示，具体过程如下：步骤3.1、旋翼无人机在绕飞轨迹下利用视觉识别分别对n个图像按时间顺序进行测量，采用sift算法对当前第i个图像进行特征提取(1≤i≤n)，然后利用模板中的特征点与当前图像的特征点进行匹配，得到w组匹配点p1,p2...pw-1,pw(w≤m)，最后取这些匹配点的几何中心pf(f≤w)代表标志物在图像中的像素位置,记为并记录在对第i个图像测量时的测量值，包括：无人机拍摄点oi在惯性参考系{i}的位置和姿态(ψi,θi,φi)，ψi,θi,φi分别为方位角，俯仰角和横滚角。步骤3.2、选取n个图像中的任意两个图像，共有n组，其中把在先测量的图像作为左视图l，在后测量的图像作为右视图r，构成旋转视图的双目视觉模型，如图3所示。计算无人机相对于标志物的相对高度hj，1≤j≤n其中，标志物在左、右视图的像素位置分别为rl，tl分别为左视图对应的无人机拍摄点ol相对于惯性参考坐标系的旋转矩阵和平移矩阵，其中，ψl,θl,φl分别为左视图无人机拍摄点ol的航向角，俯仰角和横滚角，ψr,θr,φr分别为右视图无人机拍摄点ol航向角，俯仰角和横滚角，δψ为航向偏差，有ψl＝ψi-δψ(k),k为迭代次数，θl＝θi，φl＝φi(1≤i＜n),设初始值δψ(0)＝0；rr，tr分别为右视图对应的无人机拍摄点or相对于惯性参考坐标系的旋转矩阵和平移矩阵，其中，ψr＝ψm-δψ(k)，θr＝θm，φr＝φm(i＜m≤n)左视图和右视图对应的无人机拍摄点在惯性参考坐标系下的坐标分别为和r，t为右视图对应的摄像机坐标系相对于左视图对应的摄像机坐标系的旋转矩阵、平移矩阵，r＝rrrlt，t＝tl-rttr＝rl(or-ol)；m＝[pl-rtprpl×rtpr]-1t。步骤3.3、针对计算得到的n组相对高度hj，用3σ准则剔除粗大误差，然后求n组平均值步骤3.4、获得相对高度后，利用步骤3.2中的n点测量值并基于线性回归模型计算航向偏差δψ(k)；一般地，[xyz]t，[xpypzp]t分别表示无人机和物体在惯性参考坐标系{i}的坐标，(xf′,yf′)表示物体在图像中的像素位置，f为摄像机的焦距，摄像机的测距模型为姿态矩阵为其中，h'为无人机与物体之间的相对高度，(ψ′,θ′,φ′)表示无人机在某个测量点的航向角、俯仰角和横滚角，其中，俯仰角θ′、横滚角φ′的测量精度高，其误差忽略不计，而航向角ψ′的测量存在较大的航向偏差。在本实施例中，为了计算航向角的航向偏差，利用无人机在不同位置拍摄的标志物的n点测量值，并通过线性回归方法进行求解，具体计算过程如下：[xgygzg]t表示标志物在惯性参考坐标系{i}的坐标，令[xpypzp]t＝[xgygzg]t，为无人机与标志物的相对高度的平均值，令代入公式(4)，可得设参数θ＝[θa,θb]t，θa＝[xg,yg]t，θb＝δψ(k)，位置和姿态的量测方程分别为式(6)和式(7)：z1(i)＝y1(i)+v1,v1～n(0,r1)(6)其中v1，v2为测量噪声，r1，r2为实对称正定阵。则式(5)变形为其中,为姿态偏差,运用泰勒展开，式(8)变为由式(8)和式(9)，得设矩阵其中a1,3～a2,5表示矩阵ai中对应的元素；矩阵其中b1,1～b2,3表示在矩阵bi中对应的元素。在本实施例中，对同一标志物进行n点视觉测量，故对应的矩阵为a1,…,an，b1,…,bn，通过这些测量值得到如下线性回归模型，其中，i2为2×2的单位矩阵，噪声为v～n(0,r)协方差矩阵为参数θ的估计值为通过式(12)可求解航向偏差δψ(k)。步骤3.5、设e为常数，若|δψ(k)-δψ(k-1)|＜e，则得到最终的相对高度的估计值和航向偏差的估计值并执行步骤四；否则，,转到步骤3.2，将当前的δψ(k)代入左右视图航向角的计算公式中，求出从而进行迭代计算。步骤四、在相对高度和航向偏差均有效估计的条件下，选择摄像机视野里的任一目标并获得该目标的测量值，利用得出的航向偏差计算得到无人机的真实航向，进而根据真实航向和高度估计值实现对目标的三维精确定位。具体地，假设选定的目标与标志物处于同一平面，即估计的相对高度可以认为无人机与目标的相对高度，[xtytzt]t表示目标在惯性参考坐标系{i}的坐标，有令[xpypzp]t＝[xtytzt]t，将目标的测量值以及无人机的真实航向代入公式(4)，计算得到目标的坐标，从而实现对目标的三维定位。下面具体说明该迭代过程的有效性，以绕飞轨迹是圆周为例，半径r＝73m，弧度rad＝1.5π，δψ＝0,1,...,59,60deg,由式(1)得到对应的61组然后运用数据拟合的方法，以为因变量，δψ为自变量，如图6所示，得到的数学关系表达式：相同地，令由式(10)求解获得36组δψ，然后运用数据拟合的方法，以δψ为因变量，为自变量，如图7所示，得到的数学关系表达式：设eδψ＝δψ-δψt，其中ht，δψt为相对高度和航向偏差的真实值，由式(9)得，由式(10)得，其中，k1，k2为相关参数。双目视觉模型计算的相对高度代入线性回归方程，可有效地计算航向偏差。然后，将航向偏差的估计值回代到双目视觉模型，可精确地计算相对高度。一般地，ahrs系统的航向偏差不超过30deg，所以有|k2|＞k1＞0，而由于k2＜0，根据式(15)，(16)可知，经过有限步迭代后，相对高度的估计值和航向偏差的估计值将收敛到真实值。在无人机搭载相机的条件下，进行了飞行试验，无人机在绕飞轨迹下对标志物进行图像测量，其中绕飞轨迹的半径r＝73m，弧度rad＝1.5π，无人机相对于标志物的真实高度ht＝45m，飞行速度v＝3.44m/s，fgps＝4hz，航向偏差的真实值δψt＝30deg，设e＝0.02deg，本发明所提供方法的效果如表1，表2，如图8所示。其中表中所列误差eh，eδψ，exy，ez都指的是均方根误差。表1迭代过程表2目标定位结果指标本发明的三维定位相对高度估计误差eh/m0.93航向估计误差eδψ/deg1.89定位误差exy/m10.89定位误差ez/m0.43综上所述，以上仅为本发明的较佳实施例而已，并非用于限定本发明的保护范围。凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。当前第1页12