一种获得深海大深度声场水平纵向相关性的方法与流程

本发明属于水声信号的处理方法，涉及一种获得深海大深度声场水平纵向相关性的方法，适用于深海大深度声场水平纵向相关性的定性分析和相关长度的定量估计，属于海洋工程、水声工程、阵列信号处理和声呐技术等领域。

背景技术：

海洋信道背景下的目标检测、定位、跟踪和识别，对于水下信息作战和海洋工程等领域具有重要的意义。水声信号处理的发展大致可以分为两个阶段：

(1)在第一个阶段，假设海洋信道为理想信道，积极发展自适应阵列信号处理技术来提高阵列信号处理增益。

(2)在第二个阶段，人们发现实际海洋背景下的阵列信号处理技术达不到理想性能，逐渐意识到海洋信道的复杂性，匹配场处理、基于波导不变性的处理技术等应运而生。

基于模态频散效应、波导不变量理论、声线多途特征和声场干涉周期等的单水听器目标定位技术得到了迅猛发展。但是，基于单水听器的目标定位方法往往需要较高的信噪比条件，难以满足实际需要。同时，随着潜艇减振降噪技术的发展，新型安静性潜艇的噪声级已经接近甚至低于海洋噪声的水平，这给水声信号处理提出了新的要求，因此，针对水下弱目标信号，研究基于水声物理和阵列信号处理相结合的新的目标探测和识别技术成为当下亟待解决的难题。

实际海洋应用中，常用的阵列有垂直线列阵和水平线列阵。根据锚系方式的不同，垂直线列阵有浮标和潜标两种布放形式；水平线列阵通常包含海底水平线列阵和拖曳水平线列阵。随着“深化近浅海、开拓深远海”国家战略目标的提出，可靠声路径传播条件下的目标被动探测技术得到了进一步的发展；同时，在自主航行器的辅助下，在海底布放水平线列阵成为可能。然而，目前的阵列设计方法仍然延续以阵列信号处理为导向的设计思路，基阵的绝对长度通常正比于基阵工作的最低频率对应的波长，未能充分考虑水声传播特性对信号相关性的影响，适合深海海底布放的水平线列阵的设计缺乏理论指导。

此外，无论何种形式的布放于海底附近的接收阵列，当其检测近海面运动目标时，要求信号积分时间内的信号是强相关的。目前声呐技术中信号积分时间未得到充分应用的技术瓶颈：一个是积分时间过长运动目标可能会跨越多个波束主瓣宽度，另一个原因就是信号相关长度的限制。根据声场互易性，近海面运动目标的检测问题和海底锚系水平阵列的设计问题可以归结为海底附近声场相关性的计算问题。

以往解决上述问题的方法是根据实测的海洋环境参数，结合简正波或者射线等理论，通过水声建模在线模拟声场的相关性变化规律。该方法耗费大量的计算时间，且受限于环境的复杂性，计算结果无法移植到其他海洋背景。并且计算结果无法体现出水声传播是如何影响信号相关性的。目前缺乏简明、直观且具有实际物理意义的计算方法。本发明旨在提出准确简单的相关性计算方法，为工程应用提供参考便利。

技术实现要素：

要解决的技术问题

为了避免现有技术的不足之处，本发明提出一种获得深海大深度声场水平纵向相关性的方法，适用于深海大深度接收时声场相关长度的计算。

技术方案

一种获得深海大深度声场水平纵向相关性的方法，其特征在于步骤如下：

步骤1：在深海海底附近确定两个同深度、距深度声源距离不同的接收位置作为测试位置，两个接收位置的坐标分别为(z,r)和(z,r+Δr)，z表示接收深度，r表示接收距离，Δr表示两个接收位置的水平纵向间隔；宽带深度声源的深度zs，中心频率ω0；

步骤2：利用射线模型Bellhop分别计算由宽带深度声源位置到达两个接收位置的声传播直达波和海面反射波之间的时延差Δtr和Δtr+Δr；

步骤3：将时延差Δtr和Δtr+Δr代入声场水平纵向相关计算公式进而得到声源深度为zs，接收深度为z时，两个不同接收距离r和r+Δr之间的声场水平纵向相关系数。

固定一个测试位置，沿水平方向改变另一个测试位置的距离，使得两个接收位置的水平纵向间隔Δr发生变化，然后重复步骤2和步骤3，得到声场相关性在参考接收距离为r时随水平纵向间隔的变化规律。

改变参考接收距离r，然后重复步骤2和步骤3，得到不同接收距离处的声场相关性变化规律。

所述宽带深度声源的声源深度变化范围为10～1000m。

所述宽带深度声源的频率范围为10Hz～5kHz。

所述深度声源距离接收位置的接收距离为0～30km，接收深度范围为1000～10000m。

有益效果

本发明提出的一种获得深海大深度声场水平纵向相关性的方法，在深海海底附近选取两个同深度不同距离的测试位置，根据射线模型计算某一深度声源到达两个接收位置的直达波和海面波时延差；固定一个测试位置，不断改变两个位置的水平间距，重新计算不同位置处的直达波和海面反射波的时延差；带入基于射线理论的深海大深度声场水平纵向相关计算公式，得到目标区域水平纵向相关性的变化规律。

有益效果体现在：

(1)根据公式可以描述声场相关性的定性变化规律。

(2)相比于通过繁琐的声场建模在线估算声场相关长度，本方法大大减少了计算量，易于工程实践。

附图说明

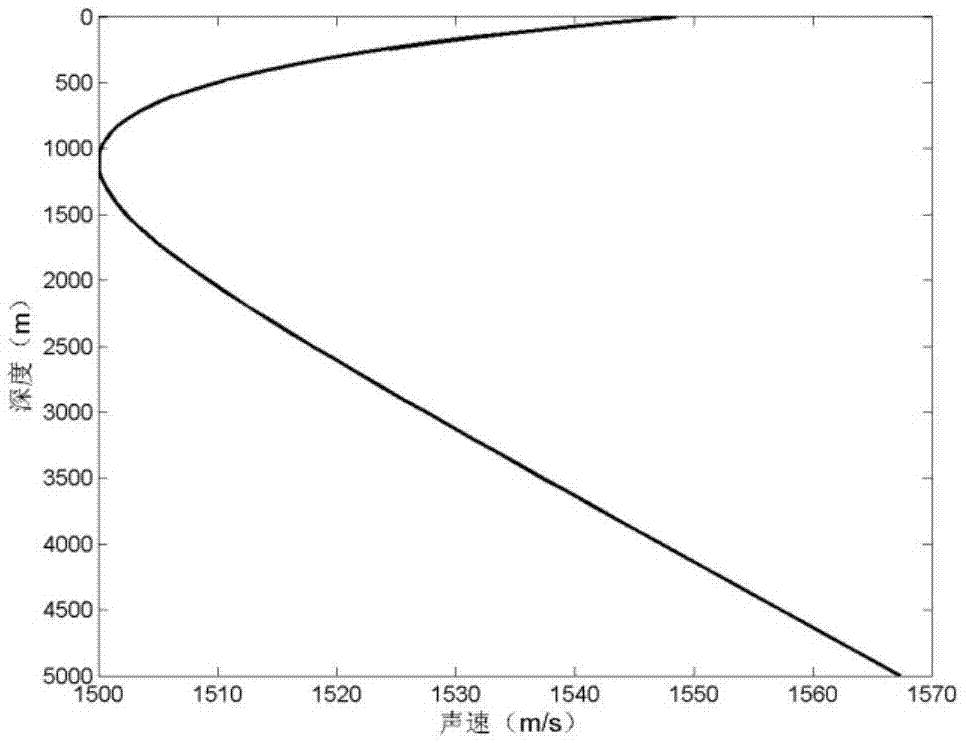
图1：仿真所用的声速剖面

图2：利用射线模型得到的直达波和海面反射波到达结构

图3：直达波和海面反射波到达时延差分布图(接收深度4700m)

图4：相关系数理论计算结果(中心频率310Hz，接收深度4700m)

(a)声源深度50m；(b)声源深度100m；(c)声源深度150m；

(d)声源深度200m；

图5：相关系数建模计算结果(声源频率260～360Hz，接收深度4700m)

(a)声源深度50m；(b)声源深度100m；(c)声源深度150m；

(d)声源深度200m；

图6：不同声源深度相关长度理论和建模计算对比结果(声源频率260～360Hz，接收深度4700m)

(a)声源深度50m；(b)声源深度100m；(c)声源深度150m；

(d)声源深度200m；

具体实施方式

现结合实施例、附图对本发明作进一步描述：

图1：仿真所用的声速剖面

计算声线直达波和海面反射波到达时延差采用典型的深海Munk剖面，其声速如图1所示。由于深海直达波区域声场主要由直达波和海面反射波贡献，我们忽略海底反射波对相关性计算的影响。

其计算过程分为以下五步：

步骤1：假设宽带声源深度zs，中心频率ω0，深海海底附近两个接收位置坐标分别为(z,r)和(z,r+Δr)，z表示接收深度，r表示接收距离，Δr表示两个接收位置的水平纵向间隔。

步骤2：利用射线模型Bellhop分别计算由声源位置到达两个接收位置的声传播直达波和海面反射波之间的时延差Δtr和Δtr+Δr。

步骤3：将计算得到的时延差Δtr和Δtr+Δr代入声场水平纵向相关计算公式进而得到声源深度为zs，接收深度为z时，两个不同接收距离r和r+Δr之间的声场水平纵向相关系数。

步骤4：改变Δr，得到声场相关性在参考接收距离为r时随水平纵向间隔的变化规律。

步骤5：改变参考接收距离r，得到不同接收距离处的声场相关性变化规律。

图2：利用射线模型得到的直达波和海面反射波到达结构

图2给出了声源深度100m时，接收距离10km、接收深度4700m处直达波和海面反射波的到达结构。其中，直达波的传播时间为7.1786s,海面反射波的传播时间为7.2284s,直达波和海面反射波的时延差为0.0498s.以下直达波和海面反射波的时延差均简称为时延差。

图3：直达波和海面反射波到达时延差分布图

图3给出了接收深度4700m时，不同声源深度在不同接收距离处的时延差分布结果。可以看出，对于固定的声源深度，接收距离越远，时延差变化越缓慢；声源深度越深，时延差随距离的变化梯度越大。所以，接收距离越远，水平纵向相关性变化越缓慢，即变化周期越大；声源深度越深，水平纵向相关性变化越剧烈，即变化周期越短。

图4：相关系数理论计算结果

根据图3所得到的时延差分布图，声场水平纵向相关系数理论计算结果如图4所示，其中中心频率ω0＝310Hz，接收深度4700m。(a)声源深度50m；(b)声源深度100m；(c)声源深度150m；(d)声源深度200m。

横轴表示计算相关性时作为参考位置的接收距离r，纵轴表示相对于参考接收位置的水平纵向间隔Δr。

图5：相关系数建模计算结果

为了验证理论计算结果的准确性，图5给出了通过数值建模得到的声场水平纵向相关系数变化结果。声源频率260～360Hz，接收深度4700m。(a)声源深度50m；(b)声源深度100m；(c)声源深度150m；(d)声源深度200m。与图4对比，可以看出理论计算结果与数值建模结果的变化规律一致，很好的预测了声场水平纵向相关性的变化趋势。

图6：不同声源深度相关长度理论和建模计算对比结果

实际应用中，当相关系数下降到0.707对应的纵向间隔定义为相关长度。当声源频率260～360Hz，接收深度4700m时，图6中黑色虚线为数值建模得到的相关长度，黑色实线为理论预测的相关长度。(a)声源深度50m；(b)声源深度100m；(c)声源深度150m；(d)声源深度200m。可以看出，本发明给出的理论解与数值建模结果一致，说明了理论计算公式的正确性。